Nos encontramos con varios problemas como el palíndromo de longitud máxima en una string, el número de substrings palindrómicas y muchos más problemas interesantes sobre las substrings palindrómicas. La mayoría de estos problemas palindrómicos de substrings tienen alguna solución DP O(n 2 ) (n es la longitud de la string dada) o luego tenemos un algoritmo complejo como el algoritmo de Manacher que resuelve los problemas palindrómicos en tiempo lineal.
En este artículo, estudiaremos una estructura de datos interesante, que resolverá todos los problemas similares anteriores de una manera mucho más simple. Esta estructura de datos es inventada por Mikhail Rubinchik .
Features of Palindromic Tree : Online query and updation
Easy to implement
Very Fast
Estructura del árbol palindrómico
La estructura real de Palindromic Tree está cerca del gráfico dirigido . En realidad, es una estructura fusionada de dos árboles que comparten algunos Nodes comunes (consulte la figura a continuación para una mejor comprensión). Los Nodes de árbol almacenan substrings palindrómicas de una string dada al almacenar sus índices.
Este árbol consta de dos tipos de aristas:
1) arista de inserción (arista ponderada)
2) sufijo palindrómico máximo (no ponderado)
Borde de inserción:
el borde de inserción de un Node u a v con algo de peso x significa que el Node v se forma insertando x al frente y al final de la string en u. Como u ya es un palíndromo, la string resultante en el Node v también será un palíndromo.
x será un solo carácter para cada borde. Por lo tanto, un Node puede tener un máximo de 26 bordes de inserción (considerando la string de letras más bajas). Usaremos el color naranja para este borde en nuestra representación pictórica.
Borde de sufijo palindrómico máximo:
como el propio nombre indica que para un Node, este borde apuntará a su Node de string de sufijo palindrómico máximo. No consideraremos la string completa en sí misma como el sufijo palindrómico máximo, ya que esto no tendrá sentido (bucles propios). Por motivos de simplicidad, lo llamaremos borde de sufijo (con lo que nos referimos al sufijo máximo excepto la string completa). Es bastante obvio que cada Node tendrá solo 1 borde de sufijo, ya que no almacenaremos strings duplicadas en el árbol. Usaremos bordes discontinuos azules para su representación pictórica.
Nodes raíz y su convención:
esta estructura de datos de árbol/gráfico contendrá 2 Nodes raíz ficticios . Más aún, considéralo precisamente como las raíces de dos árboles separados, que están unidos entre sí.
Root-1 será un Node ficticio que describirá una string de longitud = -1 (puede inferir fácilmente desde el punto de vista de la implementación por qué lo usamos). Root-2 será un Node que describirá una string nula de longitud = 0 .
Root-1 tiene un borde de sufijo conectado a sí mismo (autobucle) como para cualquier string imaginaria de longitud -1, su sufijo palindrómico máximo también será imaginario, por lo que esto está justificado. Ahora Root-2 también tendrá su borde de sufijo conectado a Root-1 ya que para una string nula (longitud 0) no hay una string de sufijo palindrómico real de longitud inferior a 0.
Construyendo el árbol palindrómico
Para construir un árbol palindrómico, simplemente insertaremos los caracteres en nuestra string uno por uno hasta llegar al final y cuando terminemos de insertar estaremos con nuestro árbol palindrómico que contendrá todas las substrings palindrómicas distintas de las strings dadas. Todo lo que debemos asegurarnos es que, en cada inserción de un nuevo carácter, nuestro árbol palindrómico mantenga la característica discutida anteriormente. Veamos cómo podemos lograrlo.
Digamos que nos dan una string s con longitud l y hemos insertado la string hasta el índice k (k < l-1). Ahora, necesitamos insertar el (k+1)-ésimo carácter. La inserción del carácter (k+1) significa la inserción de un Node que es el palíndromo más largo que termina en el índice (k+1). Entonces, la string palindrómica más larga será de la forma ( ‘s[k+1]’ + “X” + ‘s[k+1]’ ) y X en sí misma será un palíndromo. Ahora el hecho es que la string X se encuentra en el índice < k+1 y es palíndromo. Por lo tanto, ya existirá en nuestro árbol palindrómico, ya que hemos mantenido la propiedad muy básica de que contendrá todas las substrings palindrómicas distintas.
Entonces, para insertar el carácter s[k+1] , solo necesitamos encontrar la String X en nuestro árbol y dirigir el borde de inserción desde X con peso s[k+1] a un nuevo Node, que contiene s[k+ 1]+X+s[k+1] . El trabajo principal ahora es encontrar la string X en tiempo eficiente. Como sabemos, estamos almacenando el enlace de sufijo para todos los Nodes. Por lo tanto, para rastrear el Node con la string X, solo necesitamos mover hacia abajo el enlace del sufijo para el Node actual, es decir, el Node que contiene la inserción de s[k]. Vea la imagen de abajo para una mejor comprensión.
El Node actual en la siguiente figura dice que es el palíndromo más grande que termina en el índice k después de procesar todos los índices de 0 a k. La ruta punteada azul es el enlace de los bordes de sufijo del Node actual a otros Nodes procesados en el árbol. La string X existirá en uno de estos Nodes que se encuentran en esta string de enlace de sufijo. Todo lo que necesitamos es encontrarlo iterándolo a lo largo de la string.
Para encontrar el Node requerido que contiene la string X, colocaremos el carácter k+1 al final de cada Node que se encuentra en la string de enlace de sufijo y verificaremos si el primer carácter de la string de enlace de sufijo correspondiente es igual al k+1. personaje.
Una vez que encontremos la string X, dirigiremos un borde de inserción con peso s[k+1] y lo vincularemos al nuevo Node que contiene el palíndromo más grande que termina en el índice k+1. Los elementos de la array entre corchetes, como se describe en la siguiente figura, son los Nodes que se almacenan en el árbol.
Queda una cosa más por hacer. Como hemos creado un nuevo Node en esta inserción s[k+1], también tendremos que conectarlo con su sufijo link child. Una vez más, para hacerlo, usaremos lo anterior en la iteración del enlace de sufijo desde el Node X para encontrar una nueva string Y tal que s[k+1] + Y + s[k+1] sea el sufijo palindrómico más grande para el nuevo Node creado. Una vez que lo encontremos, conectaremos el enlace de sufijo de nuestro Node recién creado con el Node Y.
Nota : Hay dos posibilidades cuando encontramos la string X. La primera posibilidad es que la string s[k+1]Xs[k+1] no exista en el árbol y la segunda posibilidad es si ya existe en el árbol. En el primer caso, procederemos de la misma manera, pero en el segundo caso, no crearemos un nuevo Node por separado, sino que simplemente vincularemos el borde de inserción de X al Node S[k+1]+X+S[k+1] ya existente en el árbol. Tampoco necesitamos agregar el enlace de sufijo porque el Node ya contendrá su enlace de sufijo.
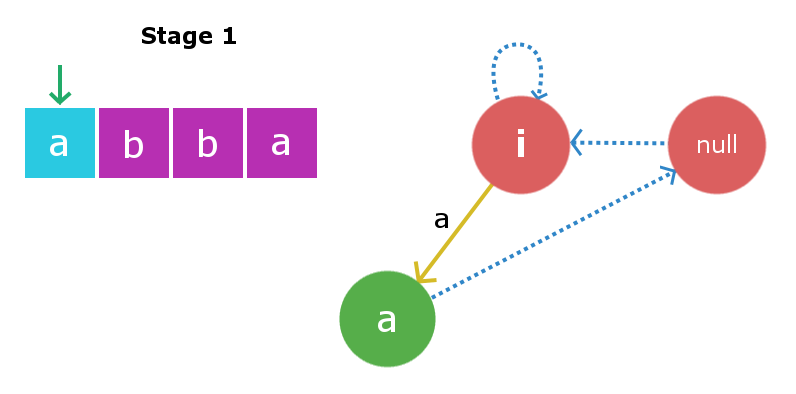
Considere una string s = » abba » con longitud = 4 .
En el estado inicial, tendremos nuestros dos Nodes raíz ficticios, uno con longitud -1 (alguna string imaginaria i ) y el segundo, una string nula con longitud 0. En este punto, no hemos insertado ningún carácter en el árbol. Root1, es decir, el Node raíz con longitud -1 será el Node actual desde el que se realiza la inserción.
Etapa 1: Insertaremos s[0] , es decir, ‘ a ‘. Comenzaremos a verificar desde el Node actual, es decir, Root1. Insertar ‘a’ al principio y al final de una string con longitud -1 producirá una string con longitud 1 y esta string será «a». Por lo tanto, creamos un nuevo Node «a» y un borde de inserción directo desde root1 a este nuevo Node. Ahora, la string de sufijo palindrómico más grande para la string de longitud 1 será una string nula, por lo que su enlace de sufijo se dirigirá a root2, es decir, string nula. Ahora el Node actual será este nuevo Node «a».
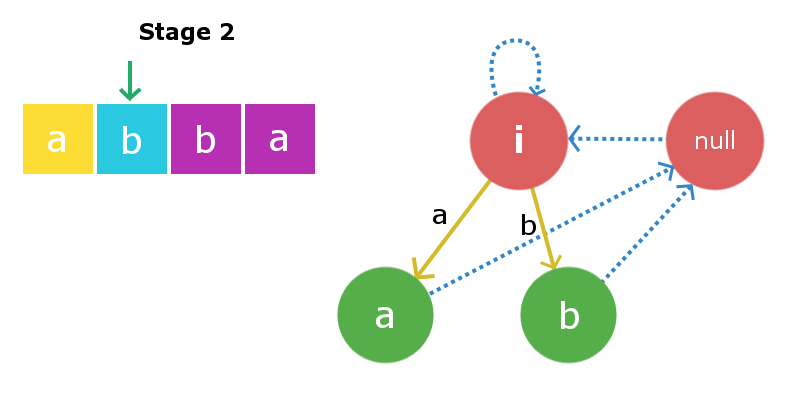
Etapa 2: Insertaremos s[1] , es decir, ‘ b ‘. El proceso de inserción comenzará desde el Node actual, es decir, el Node «a». Atravesaremos la string de enlace del sufijo comenzando desde el Node actual hasta que encontremos la string X adecuada, así que aquí, al atravesar el enlace del sufijo, nuevamente encontramos root1 como string X. Una vez más, al insertar ‘b’ en la string de longitud -1, se obtendrá una string de longitud 1, es decir, la string «b». El enlace de sufijo para este Node irá a una string nula como se describe en la inserción anterior. Ahora el Node actual será este nuevo Node “b”.
Etapa 3: Insertaremos s[2] , es decir, ‘ b ‘. Una vez más, comenzando desde el Node actual, atravesaremos su enlace de sufijo para encontrar la string X requerida. En este caso, resulta ser root2, es decir, una string nula, ya que agregar ‘b’ al principio y al final de la string nula produce un palíndromo «bb» de longitud 2. Por lo tanto, crearemos un nuevo Node » bb » y dirigiremos el borde de inserción de la string nula a la string recién creada. Ahora, el palíndromo de sufijo más grande para este Node actual será el Node «b». Entonces, vincularemos el borde del sufijo de este Node recién creado al Node «b». El Node actual ahora se convierte en el Node «bb».
Etapa 4: Insertaremos s[3] , es decir, ‘ a ‘. El proceso de inserción comienza con el Node actual y, en este caso, el Node actual en sí es la string X más grande, de modo que s[0] + X + s[3] es un palíndromo. Por lo tanto, crearemos un nuevo Node » abba » y vincularemos el borde de inserción del Node actual «bb» a este Node recién creado con peso de borde ‘a’. Ahora, el sufijo del enlace de este Node recién creado se vinculará al Node «a», ya que es el sufijo palindrómico más grande.
La implementación de C++ para la implementación anterior se proporciona a continuación:
// C++ program to demonstrate working of
// palindromic tree
#include "bits/stdc++.h"
using namespace std;
#define MAXN 1000
struct Node
{
// store start and end indexes of current
// Node inclusively
int start, end;
// stores length of substring
int length;
// stores insertion Node for all characters a-z
int insertEdg[26];
// stores the Maximum Palindromic Suffix Node for
// the current Node
int suffixEdg;
};
// two special dummy Nodes as explained above
Node root1, root2;
// stores Node information for constant time access
Node tree[MAXN];
// Keeps track the current Node while insertion
int currNode;
string s;
int ptr;
void insert(int idx)
{
//STEP 1//
/* search for Node X such that s[idx] X S[idx]
is maximum palindrome ending at position idx
iterate down the suffix link of currNode to
find X */
int tmp = currNode;
while (true)
{
int curLength = tree[tmp].length;
if (idx - curLength >= 1 and s[idx] == s[idx-curLength-1])
break;
tmp = tree[tmp].suffixEdg;
}
/* Now we have found X ....
* X = string at Node tmp
* Check : if s[idx] X s[idx] already exists or not*/
if(tree[tmp].insertEdg[s[idx]-'a'] != 0)
{
// s[idx] X s[idx] already exists in the tree
currNode = tree[tmp].insertEdg[s[idx]-'a'];
return;
}
// creating new Node
ptr++;
// making new Node as child of X with
// weight as s[idx]
tree[tmp].insertEdg[s[idx]-'a'] = ptr;
// calculating length of new Node
tree[ptr].length = tree[tmp].length + 2;
// updating end point for new Node
tree[ptr].end = idx;
// updating the start for new Node
tree[ptr].start = idx - tree[ptr].length + 1;
//STEP 2//
/* Setting the suffix edge for the newly created
Node tree[ptr]. Finding some String Y such that
s[idx] + Y + s[idx] is longest possible
palindromic suffix for newly created Node.*/
tmp = tree[tmp].suffixEdg;
// making new Node as current Node
currNode = ptr;
if (tree[currNode].length == 1)
{
// if new palindrome's length is 1
// making its suffix link to be null string
tree[currNode].suffixEdg = 2;
return;
}
while (true)
{
int curLength = tree[tmp].length;
if (idx-curLength >= 1 and s[idx] == s[idx-curLength-1])
break;
tmp = tree[tmp].suffixEdg;
}
// Now we have found string Y
// linking current Nodes suffix link with s[idx]+Y+s[idx]
tree[currNode].suffixEdg = tree[tmp].insertEdg[s[idx]-'a'];
}
// driver program
int main()
{
// initializing the tree
root1.length = -1;
root1.suffixEdg = 1;
root2.length = 0;
root2.suffixEdg = 1;
tree[1] = root1;
tree[2] = root2;
ptr = 2;
currNode = 1;
// given string
s = "abcbab";
int l = s.length();
for (int i=0; i<l; i++)
insert(i);
// printing all of its distinct palindromic
// substring
cout << "All distinct palindromic substring for "
<< s << " : \n";
for (int i=3; i<=ptr; i++)
{
cout << i-2 << ") ";
for (int j=tree[i].start; j<=tree[i].end; j++)
cout << s[j];
cout << endl;
}
return 0;
}
Producción:
All distinct palindromic substring for abcbab : 1)a 2)b 3)c 4)bcb 5)abcba 6)bab
Complejidad
de tiempo La complejidad de tiempo para el proceso de construcción será O(k*n) , aquí “ n ” es la longitud de la string y ‘ k ‘ son las iteraciones adicionales requeridas para encontrar la string X y la string Y en los enlaces de sufijo cada vez que insertamos un carácter. Intentemos aproximarnos a la constante ‘k’. Consideraremos el peor de los casos como s = “aaaaaabcccccccdeeeeeeeeeef” . En este caso, para una racha similar de caracteres continuos, se necesitarán 2 iteraciones adicionales por índice para encontrar tanto la string X como la Y en los enlaces de sufijo, pero tan pronto como alcance algún índice i tal que s[i]!=s[i- 1] el puntero más a la izquierda para el sufijo de longitud máxima alcanzará su límite más a la derecha. Por tanto, para todo i cuando s[i]!=s[i-1], costará un total de n iteraciones (sumando cada iteración) y para el resto i cuando s[i]==s[i-1] se necesitan 2 iteraciones que suman todas esas i y se necesitan 2*n iteraciones. Por lo tanto, aproximadamente nuestra complejidad en este caso será O(3*n) ~ O(n). Entonces, podemos decir aproximadamente que el factor constante ‘k’ será mucho menor. Por lo tanto, podemos considerar que la complejidad general es lineal O (longitud de la string) . Puede consultar los enlaces de referencia para una mejor comprensión.
Referencias :
Este artículo es una contribución de Nitish Kumar . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA