Hemos discutido los siguientes temas sobre el árbol rojo-negro en publicaciones anteriores. Recomendamos encarecidamente hacer referencia a la siguiente publicación como requisito previo de esta publicación.
Introducción al árbol rojo y negro Árbol rojo y
negro Insertar
Inserción frente a eliminación:
al igual que la inserción, el cambio de color y las rotaciones se utilizan para mantener las propiedades del rojo y el negro.
En la operación de inserción, comprobamos el color del tío para decidir el caso adecuado. En la operación de eliminación, comprobamos el color del hermano para decidir el caso apropiado.
La propiedad principal que viola después de la inserción son dos rojos consecutivos. En la eliminación, la principal propiedad violada es el cambio de la altura del negro en los subárboles, ya que la eliminación de un Node negro puede causar una reducción de la altura del negro en una ruta de raíz a hoja.
La eliminación es un proceso bastante complejo. Para entender la eliminación, se utiliza la noción de doble negro. Cuando se elimina un Node negro y se reemplaza por un hijo negro, el hijo se marca como doble negro . La tarea principal ahora es convertir este doble negro en un solo negro.
Pasos de eliminación
A continuación se detallan los pasos para la eliminación.
1) Realizar la eliminación estándar de BST. Cuando realizamos una operación de eliminación estándar en BST, siempre terminamos eliminando un Node que es una hoja o tiene solo un hijo (para un Node interno, copiamos el sucesor y luego recursivamente llamamos a eliminar para el sucesor, el sucesor es siempre un Node hoja o un Node con un hijo). Entonces, solo necesitamos manejar los casos en los que un Node es hoja o tiene un hijo. Sea v el Node que se eliminará y u el hijo que reemplaza a v (tenga en cuenta que u es NULL cuando v es una hoja y el color de NULL se considera negro).
2) Caso simple: si u o v son rojos, marcamos el niño reemplazado como negro (sin cambios en la altura del negro). Tenga en cuenta que tanto u como v no pueden ser rojos ya que v es el padre de u y no se permiten dos rojos consecutivos en el árbol rojo-negro.
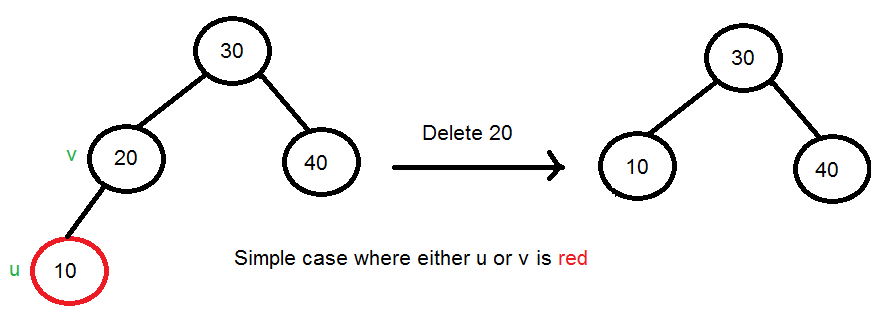
3) Si tanto u como v son negros .
3.1) Color u como doble negro. Ahora nuestra tarea se reduce a convertir este doble negro en un solo negro. Tenga en cuenta que si v es una hoja, entonces u es NULL y el color de NULL se considera negro. Entonces, la eliminación de una hoja negra también provoca un doble negro.

3.2) Haga lo siguiente mientras el Node actual u es doblemente negro y no es la raíz. Deje que el hermano del Node sea s .
…. (a): Si el hermano s es negro y al menos uno de los hijos del hermano es , realice la(s) rotación(es). Que el niño rojo de s sea. Este caso se puede dividir en cuatro subcasos dependiendo de las posiciones de s y r.
………….. (i) Left Left Case (s es hijo izquierdo de su padre y r es hijo izquierdo de s o ambos hijos de s son rojos). Este es el espejo de la carcasa derecha derecha que se muestra en el siguiente diagrama.
………….. (ii) Caso Izquierda Derecha (s es el hijo izquierdo de su padre y r es el hijo derecho). Este es el espejo de la caja izquierda derecha que se muestra en el diagrama a continuación.
………….. (iii)Right Right Case (s es hijo derecho de su padre y r es hijo derecho de s o ambos hijos de s son rojos)
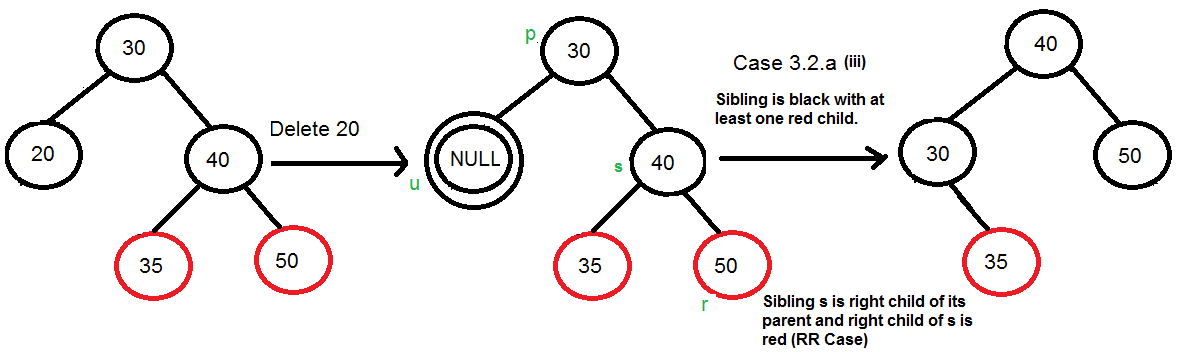
………….. (iv) Caso derecho izquierdo (s es hijo derecho de su padre y r es hijo izquierdo de s)

….. (b): Si el hermano es negro y sus dos hijos son negros , realice el cambio de color y recurra para el padre si el padre es negro.

En este caso, si el padre era rojo, entonces no necesitábamos recurrir al padre, simplemente podemos hacerlo negro (rojo + negro doble = negro simple)
….. (c): Si el hermano es , realice una rotación para mover al hermano mayor hacia arriba, volver a colorear al hermano mayor y al padre. El nuevo hermano siempre es negro (ver el diagrama a continuación). Esto convierte principalmente el árbol en un caso hermano negro (por rotación) y conduce al caso (a) o (b). Este caso se puede dividir en dos subcasos.
………….. (i) Caso Izquierdo (s es hijo izquierdo de su padre). Este es el espejo de la carcasa derecha derecha que se muestra en el siguiente diagrama. Giramos a la derecha el padre p.
………….. (ii) Caso derecho (s es hijo derecho de su padre). Dejamos rotar el padre p.

3.3) Si u es raíz, hágalo solo negro y regrese (la altura negra del árbol completo se reduce en 1).
a continuación se muestra la implementación en C++ del enfoque anterior:
CPP
#include <iostream>
#include <queue>
using namespace std;
enum COLOR { RED, BLACK };
class Node {
public:
int val;
COLOR color;
Node *left, *right, *parent;
Node(int val) : val(val) {
parent = left = right = NULL;
// Node is created during insertion
// Node is red at insertion
color = RED;
}
// returns pointer to uncle
Node *uncle() {
// If no parent or grandparent, then no uncle
if (parent == NULL or parent->parent == NULL)
return NULL;
if (parent->isOnLeft())
// uncle on right
return parent->parent->right;
else
// uncle on left
return parent->parent->left;
}
// check if node is left child of parent
bool isOnLeft() { return this == parent->left; }
// returns pointer to sibling
Node *sibling() {
// sibling null if no parent
if (parent == NULL)
return NULL;
if (isOnLeft())
return parent->right;
return parent->left;
}
// moves node down and moves given node in its place
void moveDown(Node *nParent) {
if (parent != NULL) {
if (isOnLeft()) {
parent->left = nParent;
} else {
parent->right = nParent;
}
}
nParent->parent = parent;
parent = nParent;
}
bool hasRedChild() {
return (left != NULL and left->color == RED) or
(right != NULL and right->color == RED);
}
};
class RBTree {
Node *root;
// left rotates the given node
void leftRotate(Node *x) {
// new parent will be node's right child
Node *nParent = x->right;
// update root if current node is root
if (x == root)
root = nParent;
x->moveDown(nParent);
// connect x with new parent's left element
x->right = nParent->left;
// connect new parent's left element with node
// if it is not null
if (nParent->left != NULL)
nParent->left->parent = x;
// connect new parent with x
nParent->left = x;
}
void rightRotate(Node *x) {
// new parent will be node's left child
Node *nParent = x->left;
// update root if current node is root
if (x == root)
root = nParent;
x->moveDown(nParent);
// connect x with new parent's right element
x->left = nParent->right;
// connect new parent's right element with node
// if it is not null
if (nParent->right != NULL)
nParent->right->parent = x;
// connect new parent with x
nParent->right = x;
}
void swapColors(Node *x1, Node *x2) {
COLOR temp;
temp = x1->color;
x1->color = x2->color;
x2->color = temp;
}
void swapValues(Node *u, Node *v) {
int temp;
temp = u->val;
u->val = v->val;
v->val = temp;
}
// fix red red at given node
void fixRedRed(Node *x) {
// if x is root color it black and return
if (x == root) {
x->color = BLACK;
return;
}
// initialize parent, grandparent, uncle
Node *parent = x->parent, *grandparent = parent->parent,
*uncle = x->uncle();
if (parent->color != BLACK) {
if (uncle != NULL && uncle->color == RED) {
// uncle red, perform recoloring and recurse
parent->color = BLACK;
uncle->color = BLACK;
grandparent->color = RED;
fixRedRed(grandparent);
} else {
// Else perform LR, LL, RL, RR
if (parent->isOnLeft()) {
if (x->isOnLeft()) {
// for left right
swapColors(parent, grandparent);
} else {
leftRotate(parent);
swapColors(x, grandparent);
}
// for left left and left right
rightRotate(grandparent);
} else {
if (x->isOnLeft()) {
// for right left
rightRotate(parent);
swapColors(x, grandparent);
} else {
swapColors(parent, grandparent);
}
// for right right and right left
leftRotate(grandparent);
}
}
}
}
// find node that do not have a left child
// in the subtree of the given node
Node *successor(Node *x) {
Node *temp = x;
while (temp->left != NULL)
temp = temp->left;
return temp;
}
// find node that replaces a deleted node in BST
Node *BSTreplace(Node *x) {
// when node have 2 children
if (x->left != NULL and x->right != NULL)
return successor(x->right);
// when leaf
if (x->left == NULL and x->right == NULL)
return NULL;
// when single child
if (x->left != NULL)
return x->left;
else
return x->right;
}
// deletes the given node
void deleteNode(Node *v) {
Node *u = BSTreplace(v);
// True when u and v are both black
bool uvBlack = ((u == NULL or u->color == BLACK) and (v->color == BLACK));
Node *parent = v->parent;
if (u == NULL) {
// u is NULL therefore v is leaf
if (v == root) {
// v is root, making root null
root = NULL;
} else {
if (uvBlack) {
// u and v both black
// v is leaf, fix double black at v
fixDoubleBlack(v);
} else {
// u or v is red
if (v->sibling() != NULL)
// sibling is not null, make it red"
v->sibling()->color = RED;
}
// delete v from the tree
if (v->isOnLeft()) {
parent->left = NULL;
} else {
parent->right = NULL;
}
}
delete v;
return;
}
if (v->left == NULL or v->right == NULL) {
// v has 1 child
if (v == root) {
// v is root, assign the value of u to v, and delete u
v->val = u->val;
v->left = v->right = NULL;
delete u;
} else {
// Detach v from tree and move u up
if (v->isOnLeft()) {
parent->left = u;
} else {
parent->right = u;
}
delete v;
u->parent = parent;
if (uvBlack) {
// u and v both black, fix double black at u
fixDoubleBlack(u);
} else {
// u or v red, color u black
u->color = BLACK;
}
}
return;
}
// v has 2 children, swap values with successor and recurse
swapValues(u, v);
deleteNode(u);
}
void fixDoubleBlack(Node *x) {
if (x == root)
// Reached root
return;
Node *sibling = x->sibling(), *parent = x->parent;
if (sibling == NULL) {
// No sibiling, double black pushed up
fixDoubleBlack(parent);
} else {
if (sibling->color == RED) {
// Sibling red
parent->color = RED;
sibling->color = BLACK;
if (sibling->isOnLeft()) {
// left case
rightRotate(parent);
} else {
// right case
leftRotate(parent);
}
fixDoubleBlack(x);
} else {
// Sibling black
if (sibling->hasRedChild()) {
// at least 1 red children
if (sibling->left != NULL and sibling->left->color == RED) {
if (sibling->isOnLeft()) {
// left left
sibling->left->color = sibling->color;
sibling->color = parent->color;
rightRotate(parent);
} else {
// right left
sibling->left->color = parent->color;
rightRotate(sibling);
leftRotate(parent);
}
} else {
if (sibling->isOnLeft()) {
// left right
sibling->right->color = parent->color;
leftRotate(sibling);
rightRotate(parent);
} else {
// right right
sibling->right->color = sibling->color;
sibling->color = parent->color;
leftRotate(parent);
}
}
parent->color = BLACK;
} else {
// 2 black children
sibling->color = RED;
if (parent->color == BLACK)
fixDoubleBlack(parent);
else
parent->color = BLACK;
}
}
}
}
// prints level order for given node
void levelOrder(Node *x) {
if (x == NULL)
// return if node is null
return;
// queue for level order
queue<Node *> q;
Node *curr;
// push x
q.push(x);
while (!q.empty()) {
// while q is not empty
// dequeue
curr = q.front();
q.pop();
// print node value
cout << curr->val << " ";
// push children to queue
if (curr->left != NULL)
q.push(curr->left);
if (curr->right != NULL)
q.push(curr->right);
}
}
// prints inorder recursively
void inorder(Node *x) {
if (x == NULL)
return;
inorder(x->left);
cout << x->val << " ";
inorder(x->right);
}
public:
// constructor
// initialize root
RBTree() { root = NULL; }
Node *getRoot() { return root; }
// searches for given value
// if found returns the node (used for delete)
// else returns the last node while traversing (used in insert)
Node *search(int n) {
Node *temp = root;
while (temp != NULL) {
if (n < temp->val) {
if (temp->left == NULL)
break;
else
temp = temp->left;
} else if (n == temp->val) {
break;
} else {
if (temp->right == NULL)
break;
else
temp = temp->right;
}
}
return temp;
}
// inserts the given value to tree
void insert(int n) {
Node *newNode = new Node(n);
if (root == NULL) {
// when root is null
// simply insert value at root
newNode->color = BLACK;
root = newNode;
} else {
Node *temp = search(n);
if (temp->val == n) {
// return if value already exists
return;
}
// if value is not found, search returns the node
// where the value is to be inserted
// connect new node to correct node
newNode->parent = temp;
if (n < temp->val)
temp->left = newNode;
else
temp->right = newNode;
// fix red red voilaton if exists
fixRedRed(newNode);
}
}
// utility function that deletes the node with given value
void deleteByVal(int n) {
if (root == NULL)
// Tree is empty
return;
Node *v = search(n), *u;
if (v->val != n) {
cout << "No node found to delete with value:" << n << endl;
return;
}
deleteNode(v);
}
// prints inorder of the tree
void printInOrder() {
cout << "Inorder: " << endl;
if (root == NULL)
cout << "Tree is empty" << endl;
else
inorder(root);
cout << endl;
}
// prints level order of the tree
void printLevelOrder() {
cout << "Level order: " << endl;
if (root == NULL)
cout << "Tree is empty" << endl;
else
levelOrder(root);
cout << endl;
}
};
int main() {
RBTree tree;
tree.insert(7);
tree.insert(3);
tree.insert(18);
tree.insert(10);
tree.insert(22);
tree.insert(8);
tree.insert(11);
tree.insert(26);
tree.insert(2);
tree.insert(6);
tree.insert(13);
tree.printInOrder();
tree.printLevelOrder();
cout<<endl<<"Deleting 18, 11, 3, 10, 22"<<endl;
tree.deleteByVal(18);
tree.deleteByVal(11);
tree.deleteByVal(3);
tree.deleteByVal(10);
tree.deleteByVal(22);
tree.printInOrder();
tree.printLevelOrder();
return 0;
}
Producción:
Inorder: 2 3 6 7 8 10 11 13 18 22 26 Level order: 10 7 18 3 8 11 22 2 6 13 26 Deleting 18, 11, 3, 10, 22 Inorder: 2 6 7 8 13 26 Level order: 13 7 26 6 8 2
Referencias:
https://www.cs.purdue.edu/homes/ayg/CS251/slides/chap13c.pdf
Introducción a los algoritmos 3.ª edición por Clifford Stein, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest
Por favor escriba comentarios si encuentra algo incorrecto, o si desea compartir más información sobre el tema tratado anteriormente
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA