Self-Balancing-Binary-Search-Trees (Comparaciones)

Los árboles de búsqueda binarios autoequilibrados son árboles de búsqueda binarios de altura equilibrada que mantienen automáticamente la altura lo más pequeña posible cuando se realizan operaciones de inserción y eliminación en el árbol. La altura generalmente se mantiene en el orden de Log n para que todas las operaciones tomen tiempo O (Log n) en promedio. 

Ejemplos: 
árbol negro rojo 
 

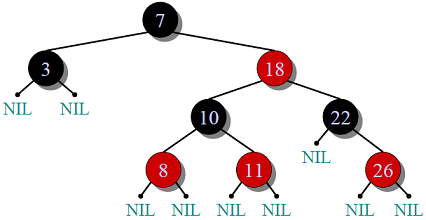
Árbol AVL: 
 

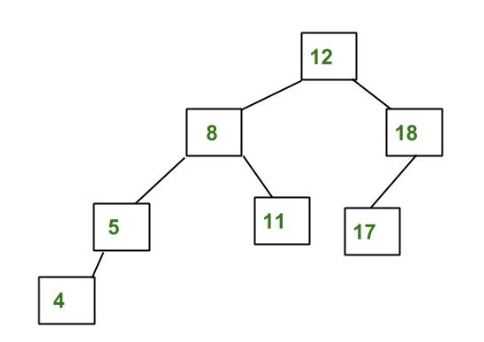
Implementaciones de lenguaje: establecer y mapear en C++ STL. TreeSet y TreeMap en Java. La mayoría de las implementaciones de la biblioteca utilizan Red Black Tree. La biblioteca estándar de Python no es compatible con Self Balancing BST. En Python, podemos usar el módulo bisect para mantener un conjunto de datos ordenados. También podemos usar módulos PyPi como rbtree (implementación del árbol rojo y negro) y pyavl (implementación del árbol AVL). 

¿Cómo mantiene la altura Self-Balancing-Tree?  
Una operación típica que realizan los árboles es la rotación. Las siguientes son dos operaciones básicas que se pueden realizar para volver a equilibrar un BST sin violar la propiedad BST (teclas (izquierda) < tecla (raíz) < teclas (derecha)). 
1) Rotación a la izquierda 
2) Rotación a la derecha 

T1, T2 and T3 are subtrees of the tree 
rooted with y (on the left side) or x (on 
the right side)           
     y                               x
    / \     Right Rotation          /  \
   x   T3   - - - - - - - >        T1   y 
  / \       < - - - - - - -            / \
 T1  T2     Left Rotation            T2  T3
Keys in both of the above trees follow the 
following order 
 keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.

Ya hemos discutido el árbol AVL , Red Black Tree y Splay Tree . En este artículo, compararemos la eficiencia de estos árboles: 
 

Métrico	Árbol RB	Árbol AVL	Árbol de juego
Inserción en el  peor de los casos	O (inicio de sesión)	O (inicio de sesión)	Amortizado O(logn)
Altura máxima  del árbol	2*registro(n)	1.44*registro(n)	En)
Buscar en  el peor de los casos	O (inicio de sesión),  moderado	O (inicio de sesión),  más rápido	O amortizado (logn),  más lento
La implementación eficiente requiere	Tres punteros con bit de color por Node	Dos punteros con factor de equilibrio por  Node	Solo dos punteros  sin información adicional
Eliminación en el  peor de los casos	O (inicio de sesión)	O (inicio de sesión)	Amortizado O(logn)
mayormente usado	Como estructura de datos universal	Cuando se requieren búsquedas frecuentes	Cuando se  recupera el mismo elemento una y otra vez
Aplicación del mundo real	Transacciones de base de datos	Multiconjunto, Multimapa, Mapa, Conjunto, etc.	Implementación de caché, Algoritmos de recolección de basura