Con la creciente popularidad de la tecnología blockchain y las criptomonedas, Merkle Trees o Hash Trees juegan un papel crucial en la verificación de la integridad de las transacciones almacenadas en el libro mayor descentralizado, con menos cantidad de datos. Somos muy conscientes de que una string de bloques está formada por «bloques» conectados a través de punteros hash y cada bloque consta de transacciones que han sido validadas y aprobadas por la mayoría de los mineros. La popularidad de los árboles Merkle ha crecido a lo largo de los años y estos se utilizan en criptomonedas como Bitcoin y Ethereum .
En este artículo, se cubrirán las propiedades del árbol de Merkle y cómo esta estructura de datos hace que la string de bloques sea inmutable y confiable. Hay algunas definiciones que deben conocerse antes de entrar en los árboles de Merkle.
Hash criptográfico
Un hash criptográfico es una función que genera un resumen de tamaño fijo para una entrada de longitud variable. Una función hash es una primitiva criptográfica importante y se usa ampliamente en blockchain. Por ejemplo, SHA-256 es una función hash en la que para cualquier entrada de longitud de bits variable, la salida siempre será un hash de 256 bits.

De la imagen de arriba, está claro que incluso el más mínimo cambio en un alfabeto en la oración de entrada puede cambiar drásticamente el hash obtenido. Por lo tanto, se pueden usar hashes para verificar la integridad .
Considere que hay un archivo de texto con datos importantes. Pase el contenido del archivo de texto a una función hash y luego almacene el hash en el teléfono. Un hacker logra abrir el archivo de texto y cambia los datos. Ahora, cuando abra el archivo nuevamente, puede calcular el hash nuevamente y comparar este hash con el almacenado previamente en el teléfono. Será claramente evidente que los dos hash no coinciden y, por lo tanto, el archivo ha sido manipulado.
Puntero hash
Un puntero normal almacena la dirección de memoria de los datos. Con este puntero, se puede acceder fácilmente a los datos. Por otro lado, un puntero hash es un puntero a donde se almacenan los datos y con el puntero también se almacena el hash criptográfico de los datos. Entonces, un puntero hash apunta a los datos y también nos permite verificar los datos. Se puede usar un puntero hash para construir todo tipo de estructuras de datos, como blockchain y el árbol de Merkle.

Estructura de la string de bloques
La string de bloques es una combinación competente de dos estructuras de datos basadas en hash:
- Lista enlazada : esta es la estructura de la propia string de bloques, que es una lista enlazada de punteros hash. Una lista enlazada normal consta de Nodes. Cada Node tiene 2 partes: datos y puntero. El puntero apunta al siguiente Node. En la string de bloques, simplemente reemplace el puntero normal con un puntero hash.
- Árbol de Merkle : un árbol de Merkle es un árbol binario formado por punteros hash y lleva el nombre de su creador, Ralph Merkle.

Blockchain como lista enlazada con punteros hash
Estructura de bloque
- Encabezado del bloque: Los datos del encabezado contienen metadatos del bloque, es decir, información sobre el propio bloque. El contenido del encabezado del bloque incluye:
- Hash del encabezado del bloque anterior
- Hash del bloque actual
- marca de tiempo
- Nonce criptográfico
- Raíz de Merkle
- Árbol de Merkle: un árbol de Merkle es un árbol binario formado por punteros hash y lleva el nombre de su creador, Ralph Merkle.
- Como se mencionó anteriormente, se supone que cada bloque contiene una cierta cantidad de transacciones. Ahora surge la pregunta, ¿cómo almacenar estas transacciones dentro de un bloque? Un enfoque puede ser formar una lista vinculada de transacciones basada en un puntero hash y almacenar esta lista vinculada completa en un bloque. Sin embargo, cuando ponemos este enfoque en perspectiva, no parece práctico almacenar una enorme lista de cientos de transacciones. ¿Qué sucede si es necesario averiguar si una transacción en particular pertenece a un bloque? Luego tendremos que recorrer los bloques uno por uno y dentro de cada bloque recorrer la lista vinculada de transacciones.
- Esta es una gran sobrecarga y puede reducir la eficiencia de la string de bloques. Ahora, aquí es donde el árbol de Merkle entra en escena. El árbol de Merkle es un árbol por bloque de todas las transacciones que se incluyen en el bloque. Nos permite tener un resumen/hash de todas las transacciones y proporciona prueba de membresía de una manera eficiente en el tiempo.
- Entonces, para recapitular, la string de bloques es una lista de bloques vinculada basada en hash, donde cada bloque consta de encabezado y transacciones. Las transacciones se organizan en forma de árbol, conocido como el árbol de Merkle.

Cada bloque se compone de encabezado de bloque + árbol de Merkle
Estructura del árbol de Merkle:

Estructura del árbol Merkle
- Una string de bloques puede tener potencialmente miles de bloques con miles de transacciones en cada bloque. Por lo tanto, el espacio de memoria y la potencia informática son dos desafíos principales.
- Sería óptimo usar la menor cantidad de datos posible para verificar las transacciones, lo que puede reducir el procesamiento de la CPU y brindar una mejor seguridad, y esto es exactamente lo que ofrecen los árboles de Merkle.
- En un árbol de Merkle, las transacciones se agrupan en pares. El hash se calcula para cada par y se almacena en el Node principal. Ahora los Nodes principales se agrupan en pares y su hash se almacena un nivel más arriba en el árbol. Esto continúa hasta la raíz del árbol. Los diferentes tipos de Nodes en un árbol de Merkle son:
- Node raíz: la raíz del árbol merkle se conoce como raíz merkle y esta raíz merkle se almacena en el encabezado del bloque.
- Node hoja: los Nodes hoja contienen los valores hash de los datos de transacción. Cada transacción en el bloque tiene sus datos hash y luego este valor hash (también conocido como ID de transacción) se almacena en Nodes hoja.
- Node no hoja: los Nodes no hoja contienen el valor hash de sus respectivos hijos. Estos también se denominan Nodes intermedios porque contienen los valores hash intermedios y el proceso hash continúa hasta la raíz del árbol.
- Bitcoin utiliza la función hash SHA-256 para codificar los datos de las transacciones de forma continua hasta que se obtiene la raíz de Merkle.
- Además, un árbol de Merkle es de naturaleza binaria . Esto significa que la cantidad de Nodes hoja debe ser uniforme para que el árbol de Merkle se construya correctamente. En caso de que haya un número impar de Nodes hoja, el árbol duplica el último hash y hace que el número de Nodes hoja sea par.
¿Cómo funcionan los árboles Merkle?
- Un árbol Merkle se construye desde el nivel de los Nodes hoja hasta el nivel raíz de Merkle agrupando los Nodes en pares y calculando el hash de cada par de Nodes en ese nivel en particular. Este valor hash se propaga al siguiente nivel. Este es un tipo de construcción de abajo hacia arriba donde los valores hash fluyen de abajo hacia arriba.
- Por lo tanto, al comparar la estructura de árbol de Merkle con una estructura de datos de árbol binario regular, se puede observar que los árboles de Merkle en realidad están invertidos hacia abajo .
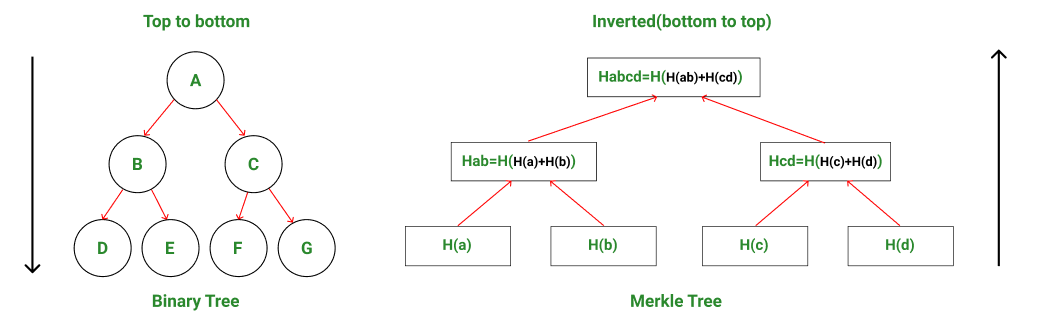
Dirección del árbol binario frente a la dirección del árbol Merkle
Ejemplo: Considere un bloque que tiene 4 transacciones: T1, T2, T3, T4. Estas cuatro transacciones deben almacenarse en el árbol de Merkle y esto se realiza mediante los siguientes pasos:
Paso 1: se calcula el hash de cada transacción.
H1 = hash (T1).
Paso 2: los hash calculados se almacenan en Nodes hoja del árbol de Merkle.
Paso 3: ahora se formarán Nodes que no sean hojas. Para formar estos Nodes, los Nodes hoja se emparejarán de izquierda a derecha y se calculará el hash de estos pares. En primer lugar, se calculará el hash de H1 y H2 para formar H12. De manera similar, se calcula H34. Los valores H12 y H34 son Nodes principales de H1, H2 y H3, H4 respectivamente. Estos no son Nodes de hoja.
H12 = Hachís (H1 + H2)
H34 = Hachís (H3 + H4)
Paso 4: finalmente se calcula H1234 emparejando H12 y H34. H1234 es el único hash que queda. Esto significa que hemos llegado al Node raíz y, por lo tanto, H1234 es la raíz de merkle.
H1234 = Hachís (H12 + H34)

El árbol de Merkle funciona mediante el hash de los Nodes secundarios una y otra vez hasta que solo queda un hash.
Puntos clave:
- Para verificar si la transacción ha sido manipulada dentro del árbol, solo es necesario recordar la raíz del árbol.
- Se puede acceder a las transacciones atravesando los punteros hash y si se ha cambiado algún contenido en la transacción, esto se reflejará en el hash almacenado en el Node principal, lo que a su vez afectaría el hash en el Node de nivel superior y así sucesivamente. hasta llegar a la raíz.
- Por lo tanto, la raíz del árbol Merkle también ha cambiado. Por lo tanto, Merkle Root, que se almacena en el encabezado del bloque, hace que las transacciones sean a prueba de manipulaciones y valida la integridad de los datos.
- Con la ayuda de merkle root, merkle tree ayuda a eliminar transacciones duplicadas o falsas en un bloque.
- Genera una huella digital de todas las transacciones en un bloque y la raíz de merkle en el encabezado está más protegida por el hash del encabezado del bloque almacenado en el siguiente bloque.
¿Por qué Merkle Trees son importantes para Blockchain?
- En una red centralizada, se puede acceder a los datos desde una sola copia. Esto significa que los Nodes no tienen que asumir la responsabilidad de almacenar sus propias copias de datos y los datos se pueden recuperar rápidamente.
- Sin embargo, la situación no es tan simple en un sistema distribuido.
- Consideremos un escenario en el que blockchain no tiene árboles merkle. En este caso, cada Node de la red deberá mantener un registro de cada transacción que haya ocurrido porque no hay una copia central de la información.
- Esto significa que se deberá almacenar una gran cantidad de información en cada Node y cada Node tendrá su propia copia del libro mayor. Si un Node quiere validar una transacción pasada, se deberán enviar requests a todos los Nodes, solicitando su copia del libro mayor. Luego, el usuario deberá comparar su propia copia con las copias obtenidas de varios Nodes.
- Cualquier desajuste podría comprometer la seguridad de blockchain. Más adelante, tales requests de verificación requerirán que se envíen grandes cantidades de datos a través de la red, y la computadora que realiza esta verificación necesitará mucha potencia de procesamiento para comparar diferentes versiones de libros de contabilidad.
- Sin el árbol de Merkle, ellos datos en sí tienen que ser transferidos por toda la red para su verificación.
- Los árboles de Merkle permiten la comparación y verificación de transacciones con potencia computacional y ancho de banda viables . Solo es necesario enviar una pequeña cantidad de información, lo que compensa los enormes volúmenes de datos contables que debían intercambiarse anteriormente.
Los árboles de Merkle utilizan ampliamente una función hash unidireccional y este hash separa la prueba de los datos de los datos en sí.
Prueba de membresía:
Una característica muy interesante del árbol de Merkle es que proporciona prueba de membresía .
Ejemplo: un minero quiere probar que una transacción en particular pertenece a un Merkletree. Ahora el minero necesita presentar esta transacción y todos los Nodes que se encuentran en el camino entre la transacción y la raíz. El resto del árbol se puede ignorar porque los valores hash almacenados en los Nodes intermedios son suficientes para verificar los valores hash hasta la raíz.

Prueba de membresía: verificar la presencia de transacciones en bloques utilizando el árbol Merkle.
Si hay n Nodes en el árbol, solo se deben examinar los Nodes log(n). Por lo tanto, incluso si hay una gran cantidad de Nodes en el árbol de Merkle, la prueba de membresía se puede calcular en un tiempo relativamente corto.
Pruebas de Merkle:
Se utiliza una prueba de Merkle para decidir:
- Si los datos pertenecen a un árbol de Merkle en particular.
- Demostrar que los datos pertenecen a un conjunto sin necesidad de almacenar todo el conjunto.
- Para probar que ciertos datos están incluidos en un conjunto de datos más grande sin revelar el conjunto de datos más grande o sus subconjuntos.
Las pruebas de Merkle se establecen mezclando el hash correspondiente de un hash y trepando por el árbol hasta obtener el hash raíz que es o puede ser conocido públicamente.
Considere el árbol de Merkle que se muestra a continuación:

Digamos que necesitamos probar que la transacción ‘a’ es parte de este árbol de Merkle. Todos en la red estarán al tanto de la función hash utilizada por todos los árboles de Merkle.
- H(a) = Ha según el diagrama.
- El hash de Ha y Hb será Hab, que se almacenará en un Node de nivel superior.
- Finalmente hash de Hab y Hcd darán Habcd. Esta es la raíz de merkle obtenida por nosotros.
- Al comparar la raíz Merkle obtenida y la raíz Merkle ya disponible dentro del encabezado del bloque, podemos verificar la presencia de la transacción ‘a’ en este bloque.
Del ejemplo anterior, es claro que para verificar la presencia de ‘a’, no es necesario revelar ‘a’ ni ‘b’, ‘c’, ‘d’, solo sus valores hash. Son suficientes. Por lo tanto, la prueba de Merkle proporciona un método eficiente y simple para verificar la inclusión y es sinónimo de «prueba de inclusión».
Un árbol de Merkle ordenado es un árbol en el que todos los bloques de datos se ordenan mediante una función de ordenación. Esta ordenación puede ser alfabética, lexicográfica, numérica, etc.
Prueba de no membresía:
- También es posible probar la no pertenencia en tiempo y espacio logarítmicos utilizando un árbol de Merkle ordenado. Es decir, es posible mostrar que una determinada transacción no pertenece al árbol de Merkle.
- Esto se puede hacer mostrando una ruta a la transacción que está inmediatamente antes de la transacción en cuestión, así como una ruta al artículo que está inmediatamente después.
- Si estos dos elementos en el árbol son secuenciales, esto demuestra que el elemento en cuestión no está incluido o, de lo contrario, tendría que ir entre las dos cosas que se muestran si estuviera incluido, pero no hay espacio entre ellos porque son secuenciales.
Transacción Coinbase:
Una transacción de base de monedas es una transacción de Bitcoin única que se incluye en el árbol Merkle de cada bloque en la string de bloques. Es responsable de crear nuevas monedas y también consta de un parámetro de base de monedas que los mineros pueden usar para insertar datos arbitrarios en la string de bloques.
Ventajas de Merkle Tree:
- Verificación eficiente : los árboles de Merkle ofrecen una verificación eficiente de la integridad y validez de los datos y reducen significativamente la cantidad de memoria necesaria para la verificación. La prueba de verificación no requiere que se transmita una gran cantidad de datos a través de la red blockchain. Habilite la transferencia sin confianza de criptomonedas en el sistema distribuido de igual a igual mediante la verificación rápida de las transacciones.
- Sin demora: no hay demora en la transferencia de datos a través de la red. Los árboles Merkle se utilizan ampliamente en los cálculos que mantienen el funcionamiento de las criptomonedas.
- Menos espacio en disco: los árboles Merkle ocupan menos espacio en disco en comparación con otras estructuras de datos.
- Transferencia de datos inalterada: la raíz de Merkle ayuda a garantizar que los bloques enviados a través de la red estén completos e inalterados.
- Detección de manipulación : el árbol Merkle brinda una ventaja increíble a los mineros para verificar si se ha manipulado alguna transacción.
- Dado que las transacciones se almacenan en un árbol Merkle que almacena el hash de cada Node en el Node principal superior, cualquier cambio en los detalles de la transacción, como el monto a debitar o la dirección a la que se debe realizar el pago, entonces el el cambio se propagará a los hashes en los niveles superiores y finalmente a la raíz de Merkle.
- El minero puede comparar la raíz de Merkle en el encabezado con la raíz de Merkle almacenada en la parte de datos de un bloque y puede detectar fácilmente esta manipulación.
- Complejidad de tiempo : el árbol de Merkle es la mejor solución si se realiza una comparación entre la complejidad de tiempo de buscar una transacción en un bloque que es un árbol de Merkle y otro bloque que tiene transacciones organizadas en una lista vinculada, entonces:
- Búsqueda de Merkle Tree- O (logn)
- Búsqueda de lista enlazada- O(n)
- donde n es el número de transacciones en un bloque.
Verificación de pago simple (SPV):
- SPV hace que sea extremadamente fácil para un cliente verificar si una transacción en particular existe en un bloque y es válida sin tener que descargar toda la string de bloques. Los usuarios solo requerirán una copia de los encabezados de bloque de la string más larga.
- Esta copia de encabezados se almacena en la billetera SPV y esta billetera usa el cliente SPV para vincular una transacción a una sucursal de Merkle en un bloque. El cliente de SPV solicita una prueba de inclusión (prueba de Merkle), en forma de una sucursal de Merkle. El hecho de que la transacción se pueda vincular a una sucursal de Merkle es prueba de que la transacción existe.
- Ahora, al evaluar los bloques que se extraen sobre el bloque de la transacción, el cliente también puede concluir que la mayoría de los Nodes han construido más bloques sobre esta string mediante el uso de mecanismos de consenso como Prueba de trabajo y, por lo tanto, este es el más largo. , string de bloques válida.