Área máxima del cuadrilátero

Dados los cuatro lados del cuadrilátero a, b, c, d, encuentre el área máxima posible del cuadrilátero a partir de los lados dados.
Ejemplos: 
 

Input : 1 2 1 2
Output : 2.00
It is optimal to construct a rectangle for maximum area .

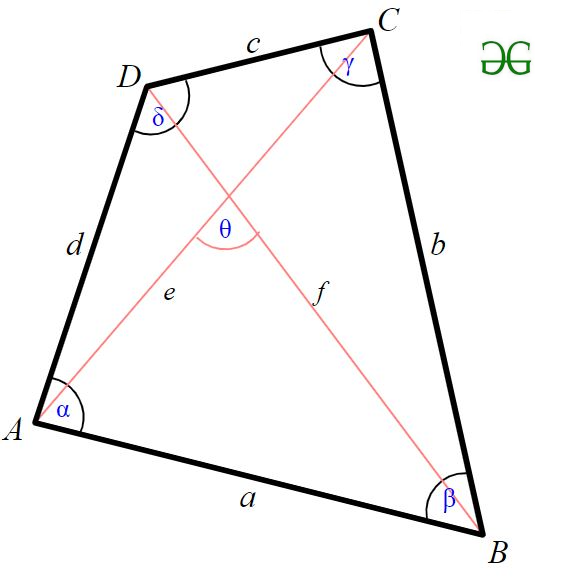
Según la fórmula de Bretschneider , el área de un cuadrilátero general viene dada por 
Aquí a, b, c, d son los lados de un cuadrilátero, s es el semiperímetro de un cuadrilátero y los ángulos son dos ángulos opuestos. 
Entonces, esta fórmula se maximiza solo cuando los ángulos opuestos suman pi (180), entonces podemos usar una forma simplificada de la fórmula de Bretschneider para obtener el área (máxima) K. 

Esta fórmula se llama fórmula de Brahmagupta . 
A continuación se muestra la implementación del enfoque dado.
 

// CPP program to find maximum area of a
// quadrilateral
#include <iostream>
#include <math.h>
using namespace std;
  
double maxArea(double a, double b,
                double c, double d)
{
    // Calculating the semi-perimeter
    // of the given quadrilateral
    double semiperimeter = (a + b + c + d) / 2;
  
    // Applying Brahmagupta's formula to
    // get maximum area of quadrilateral
    return sqrt((semiperimeter - a) *
                (semiperimeter - b) *
                (semiperimeter - c) *
                (semiperimeter - d));
}
  
// Driver code
int main()
{
    double a = 1, b = 2, c= 1, d = 2;
   cout <<maxArea(a, b, c, d);
    return 0;
}
 
// This code is contributed by shivanisinghss2110

// CPP program to find maximum area of a
// quadrilateral
#include <stdio.h>
#include <math.h>
  
double maxArea(double a, double b,
                double c, double d)
{
    // Calculating the semi-perimeter
    // of the given quadrilateral
    double semiperimeter = (a + b + c + d) / 2;
  
    // Applying Brahmagupta's formula to
    // get maximum area of quadrilateral
    return sqrt((semiperimeter - a) *
                (semiperimeter - b) *
                (semiperimeter - c) *
                (semiperimeter - d));
}
  
// Driver code
int main()
{
    double a = 1, b = 2, c= 1, d = 2;
    printf("%.2f\n",maxArea(a, b, c, d));
    return 0;
}

// Java program to find maximum area of a
// quadrilateral
import java.io.*;
 
class GFG
{
    static double maxArea(double a, double b,
                           double c, double d)
    {
        // Calculating the semi-perimeter
        // of the given quadrilateral
        double semiperimeter = (a + b + c + d) / 2;
     
        // Applying Brahmagupta's formula to
        // get maximum area of quadrilateral
        return Math.sqrt((semiperimeter - a) *
                         (semiperimeter - b) *
                         (semiperimeter - c) *
                         (semiperimeter - d));
    }
     
    // Driver code
    public static void main (String[] args)
    {
        double a = 1, b = 2, c= 1, d = 2;
        System.out.println(maxArea(a, b, c, d));
    }
}
 
// This code is contributed by sunnysingh

# Python3 program to find maximum
# area of a quadrilateral
import math
 
def maxArea (a , b , c , d ):
 
    # Calculating the semi-perimeter
    # of the given quadrilateral
    semiperimeter = (a + b + c + d) / 2
     
    # Applying Brahmagupta's formula to
    # get maximum area of quadrilateral
    return math.sqrt((semiperimeter - a) *
                    (semiperimeter - b) *
                    (semiperimeter - c) *
                    (semiperimeter - d))
 
# Driver code
a = 1
b = 2
c = 1
d = 2
print("%.2f"%maxArea(a, b, c, d))
 
# This code is contributed by "Sharad_Bhardwaj".

// C# program to find maximum area of a
// quadrilateral
using System;
 
class GFG {
     
    static double maxArea(double a, double b,
                          double c, double d)
    {
         
        // Calculating the semi-perimeter
        // of the given quadrilateral
        double semiperimeter = (a + b + c + d) / 2;
     
        // Applying Brahmagupta's formula to
        // get maximum area of quadrilateral
        return Math.Sqrt((semiperimeter - a) *
                         (semiperimeter - b) *
                         (semiperimeter - c) *
                         (semiperimeter - d));
    }
     
    // Driver code
    public static void Main ()
    {
        double a = 1, b = 2, c= 1, d = 2;
         
        Console.WriteLine(maxArea(a, b, c, d));
    }
}
 
// This code is contributed by vt_m.

<?php
// PHP program to find maximum area of a
// quadrilateral
 
function maxArea( $a, $b, $c, $d)
{
     
    // Calculating the semi-perimeter
    // of the given quadrilateral
    $semiperimeter = ($a + $b + $c + $d) / 2;
 
    // Applying Brahmagupta's formula to
    // get maximum area of quadrilateral
    return sqrt(($semiperimeter - $a) *
                ($semiperimeter - $b) *
                ($semiperimeter - $c) *
                ($semiperimeter - $d));
}
 
// Driver code
$a = 1; $b = 2; $c= 1; $d = 2;
echo(maxArea($a, $b, $c, $d));
 
// This code is contributed by vt_m.
?>

<script>
 
// JavaScript program to find maximum area of a
// quadrilateral
 
function maxArea(a, b, c, d)
{
    // Calculating the semi-perimeter
    // of the given quadrilateral
    let semiperimeter = (a + b + c + d) / 2;
 
    // Applying Brahmagupta's formula to
    // get maximum area of quadrilateral
    return Math.sqrt((semiperimeter - a) *
                (semiperimeter - b) *
                (semiperimeter - c) *
                (semiperimeter - d));
}
 
// Driver code
 
    let a = 1, b = 2, c= 1, d = 2;
    document.write(maxArea(a, b, c, d));
 
// This code is contributed by Surbhi Tyagi.
 
</script>

Producción:  

2.00

Complejidad de tiempo: O(logn) 
Espacio auxiliar: O(1)

Sugiera si alguien tiene una mejor solución que sea más eficiente en términos de espacio y tiempo.
Este artículo es una contribución de Aarti_Rathi . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.