Modelado de temas:
El modelado de temas es una forma de modelado abstracto para descubrir los ‘temas’ abstractos que ocurren en las colecciones de documentos. La idea es que realizaremos una clasificación no supervisada en diferentes documentos, que encuentran algunos grupos naturales en los temas. Podemos responder a la siguiente pregunta utilizando el modelado de temas.
- ¿Cuál es el tema/idea principal del documento?
- Dado un documento, ¿podemos encontrar otro documento con un tema similar?
- ¿Cómo cambia el campo de temas con el tiempo?
El modelado de temas puede ayudar a optimizar el proceso de búsqueda. En este artículo, discutiremos la asignación latente de Dirichlet, un proceso de modelado de temas.
Asignación latente de Dirichlet
La asignación latente de Dirichlet es uno de los métodos más populares para realizar el modelado de temas. Cada documento consta de varias palabras y cada tema se puede asociar con algunas palabras. El objetivo detrás de la LDA es encontrar temas a los que pertenece el documento, sobre la base de las palabras que contiene. Asume que los documentos con temas similares utilizarán un grupo similar de palabras. Esto permite que los documentos mapeen la distribución de probabilidad sobre temas latentes y los temas son distribución de probabilidad.
Configuración del modelo generativo:
- Supongamos que tenemos documentos D que usan el vocabulario de tipos de palabras V. Cada documento consta de un token de N palabras (se puede eliminar o rellenar). Ahora, asumimos K temas, esto requiere un vector K-dimensional que represente la distribución de temas para el documento.
- Cada tema tiene un beta_k multinomial V-dimensional sobre palabras con un previo simétrico común.
- Para cada tema 1…k:
- Dibuja un multinomio sobre palabras
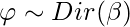 .
.
- Dibuja un multinomio sobre palabras
- Para cada documento 1…d:
- Dibujar un multinomio sobre temas
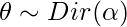
- Para cada palabra
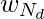 :
:
- Dibujar un tema
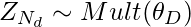 con
con ![Rendered by QuickLaTeX.com Z_{N_d} \epsilon [1..K]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c257571e9c0a9f3d0affc496421b1eb5_l3.png)
- Dibuja una palabra W_{N_d} \sim Mult(\varphi).
- Dibujar un tema
- Dibujar un multinomio sobre temas
Modelo gráfico de LDA:
![]()

- En la ecuación anterior, el LHS representa la probabilidad de generar el documento original desde la máquina LDA.
- En el lado derecho de la ecuación, hay 4 términos de probabilidad, los primeros dos términos representan la distribución de Dirichlet y los otros dos representan la distribución multinomial. Los términos primero y tercero representan la distribución de temas, pero el segundo y el cuarto representan la distribución de palabras. Discutiremos primero la distribución de Dirichlet.
Distribución Dirichlet
- La distribución de Dirichlet se puede definir como una densidad de probabilidad para una entrada con valores vectoriales que tiene las mismas características que nuestro parámetro multinomial
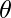 . Tiene valores distintos de cero tales que:
. Tiene valores distintos de cero tales que:
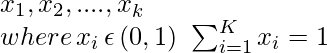
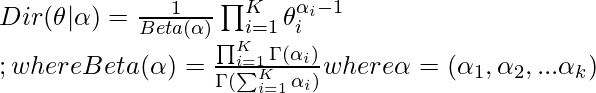
- α K θ
- p θ|α θ α?”.

Distribución de Dirichlet
- Arriba está la visualización de la distribución de Dirichlet, para nuestro propósito, podemos asumir que las esquinas/vértices representan los temas con palabras dentro del triángulo (la palabra está más cerca del tema si se relaciona frecuentemente con él) o viceversa.
- Esta distribución se puede extender a más de 3 dimensiones. Para 4 dimensiones podemos usar tetraedro y para más dimensiones. Podemos usar k-1 dimensiones simplex.
Inferencia:
- El problema de inferencia en LDA para calcular el posterior de las variables ocultas dado el documento y el parámetro del corpus \alpha y \beta. Eso es para calcular el P(
Ejemplo:
- Consideremos que tenemos dos categorías de temas, tenemos un vector de palabras para cada tema que consta de algunas palabras. Las siguientes son las palabras que representan diferentes temas:
| palabras | P(palabras | tema =1) | P(palabras | tema =2) |
|---|---|---|
| Corazón | 0.2 | 0 |
| Amor | 0.2 | 0 |
| Alma | 0.2 | 0 |
| Lágrimas | 0.2 | 0 |
| Alegría | 0.2 | 0 |
| Científico | 0 | 0.2 |
| Conocimiento | 0 | 0.2 |
| Trabajar | 0 | 0.2 |
| Investigar | 0 | 0.2 |
| Matemáticas | 0 | 0.2 |
- Ahora, tenemos un documento y escaneamos algunos documentos en busca de estas palabras:
| Palabras en el documento | {P(tema=1), P(tema=2)} |
|---|---|
| TRABAJO DE INVESTIGACIÓN DE CONOCIMIENTOS DE MATEMÁTICAS TRABAJO DE INVESTIGACIÓN DE MATEMÁTICAS TRABAJO DE MATEMÁTICAS CIENTÍFICAS | {1,0} |
| CONOCIMIENTO CIENTÍFICO MATEMÁTICAS CORAZÓN CIENTÍFICO LÁGRIMAS DE AMOR CORAZÓN DE CONOCIMIENTO | {0,25, 0,75} |
| MATEMÁTICAS CORAZÓN INVESTIGACIÓN AMOR MATEMÁTICAS TRABAJO LÁGRIMAS ALMA CONOCIMIENTO CORAZÓN | {0.5, 0.5} |
| TRABAJO ALEGRÍA ALMA LÁGRIMAS MATEMÁTICAS LÁGRIMAS AMOR AMOR AMOR ALMA | {0,75, 0,25} |
| LÁGRIMAS AMOR ALEGRÍA ALMA AMOR LÁGRIMAS ALMA ALMA LÁGRIMAS ALEGRÍA | {1,0} |
- Ahora, actualizamos las palabras anteriores a la array de temas utilizando las probabilidades de la array del documento a continuación.
Implementación
En esta implementación, usamos scikit-learn y pyLDAvis. Para los conjuntos de datos, utilizamos conjuntos de datos de reseñas de Yelp que se pueden encontrar en el sitio web de Yelp.
Python3
# install pyldavis
!pip install pyldavis
# imports
!pip install gensim pyLDAvis
! python3 -m spacy download en_core_web_sm
import pandas as pd
import numpy as np
import string
import spacy
import nltk
import gensim
from gensim import corpora
import matplotlib.pyplot as plt
import pyLDAvis
import pyLDAvis.gensim_models
nltk.download('wordnet')
from nltk.corpus import wordnet as wn
nltk.download('stopwords')
from nltk.corpus import stopwords
import spacy.cli
spacy.cli.download("en_core_web_md")
import en_core_web_md
# fetch yelp review dataset and clean it
yelp_review = pd.read_csv('/content/yelp.csv')
yelp_review.head()
# print number of document and topics
print(len(yelp_review))
print("Unique Business")
print(len(yelp_review.groupby('business_id')))
print("Unique User")
print(len(yelp_review.groupby('user_id')))
# clean the document and remove punctuation
def clean_text(text):
delete_dict = {sp_char: '' for sp_char in string.punctuation}
delete_dict[' '] =' '
table = str.maketrans(delete_dict)
text1 = text.translate(table)
textArr= text1.split()
text2 = ' '.join([w for w in textArr if ( not w.isdigit() and
( not w.isdigit() and len(w)>3))])
return text2.lower()
yelp_review['text'] = yelp_review['text'].apply(clean_text)
yelp_review['Num_words_text'] = yelp_review['text'].apply(lambda x:len(str(x).split()))
print('-------Reviews By Stars --------')
print(yelp_review['stars'].value_counts())
print(len(yelp_review))
print('-------------------------')
max_review_data_sentence_length = yelp_review['Num_words_text'].max()
# print short review (
mask = (yelp_review['Num_words_text'] < 100) & (yelp_review['Num_words_text'] >=20)
df_short_reviews = yelp_review[mask]
df_sampled = df_short_reviews.groupby('stars')
.apply(lambda x: x.sample(n=100)).reset_index(drop = True)
print('No of Short reviews')
print(len(df_short_reviews))
# function to remove stopwords
def remove_stopwords(text):
textArr = text.split(' ')
rem_text = " ".join([i for i in textArr if i not in stop_words])
return rem_text
# remove stopwords from the text
stop_words = stopwords.words('english')
df_sampled['text']=df_sampled['text'].apply(remove_stopwords)
# perform Lemmatization
lp = en_core_web_md.load(disable=['parser', 'ner'])
def lemmatization(texts,allowed_postags=['NOUN', 'ADJ']):
output = []
for sent in texts:
doc = nlp(sent)
output.append([token.lemma_
for token in doc if token.pos_ in allowed_postags ])
return output
text_list=df_sampled['text'].tolist()
print(text_list[2])
tokenized_reviews = lemmatization(text_list)
print(tokenized_reviews[2])
# convert to document term frequency:
dictionary = corpora.Dictionary(tokenized_reviews)
doc_term_matrix = [dictionary.doc2bow(rev) for rev in tokenized_reviews]
# Creating the object for LDA model using gensim library
LDA = gensim.models.ldamodel.LdaModel
# Build LDA model
lda_model = LDA(corpus=doc_term_matrix, id2word=dictionary,
num_topics=10, random_state=100,
chunksize=1000, passes=50,iterations=100)
# print lda topics with respect to each word of document
lda_model.print_topics()
# calculate perplexity and coherence
print('\Perplexity: ', lda_model.log_perplexity(doc_term_matrix,
total_docs=10000))
# calculate coherence
coherence_model_lda = CoherenceModel(model=lda_model,
texts=tokenized_reviews, dictionary=dictionary ,
coherence='c_v')
coherence_lda = coherence_model_lda.get_coherence()
print('Coherence: ', coherence_lda)
# Now, we use pyLDA vis to visualize it
pyLDAvis.sklearn.prepare(lda_tf, dtm_tf, tf_vectorizer)
Total reviews 10000 Unique Business 4174 Unique User 6403 -------------- -------Reviews by stars -------- 4 3526 5 3337 3 1461 2 927 1 749 Name: stars, dtype: int64 10000 ------------------------- No of Short reviews 6276 ------------------------- # review and tokenized version decided completely write place three times tried closed website posted hours open wants drive suburbs youd better call first place cannot trusted wasted time spent hungry minutes walking disappointed vitamin fail said ['place', 'time', 'closed', 'website', 'hour', 'open', 'drive', 'suburb', 'first', 'place', 'time', 'hungry', 'minute', 'vitamin'] --------------------------- # LDA print topics [(0, '0.015*"food" + 0.013*"good" + 0.010*"gelato" + 0.008*"sandwich" + 0.008*"chocolate" + 0.005*"wife" + 0.005*"next" + 0.005*"bad" + 0.005*"night" + 0.005*"sauce"'), (1, '0.030*"food" + 0.021*"great" + 0.019*"place" + 0.019*"good" + 0.016*"service" + 0.011*"time" + 0.011*"nice" + 0.008*"lunch" + 0.008*"dish" + 0.007*"staff"'), (2, '0.023*"food" + 0.023*"good" + 0.018*"place" + 0.014*"great" + 0.009*"star" + 0.009*"service" + 0.008*"store" + 0.007*"salad" + 0.007*"well" + 0.006*"pizza"'), (3, '0.035*"good" + 0.025*"place" + 0.023*"food" + 0.020*"time" + 0.015*"service" + 0.012*"great" + 0.009*"friend" + 0.008*"table" + 0.008*"chicken" + 0.007*"hour"'), (4, '0.020*"food" + 0.019*"time" + 0.012*"good" + 0.009*"restaurant" + 0.009*"great" + 0.008*"service" + 0.007*"order" + 0.006*"small" + 0.006*"hour" + 0.006*"next"'), (5, '0.012*"drink" + 0.009*"star" + 0.006*"worth" + 0.006*"place" + 0.006*"friend" + 0.005*"great" + 0.005*"kid" + 0.005*"drive" + 0.005*"simple" + 0.005*"experience"'), (6, '0.024*"place" + 0.015*"time" + 0.012*"food" + 0.011*"price" + 0.009*"good" + 0.009*"great" + 0.009*"kid" + 0.008*"staff" + 0.008*"nice" + 0.007*"happy"'), (7, '0.028*"place" + 0.019*"service" + 0.015*"good" + 0.014*"pizza" + 0.014*"time" + 0.013*"food" + 0.013*"great" + 0.011*"well" + 0.009*"order" + 0.007*"price"'), (8, '0.032*"food" + 0.026*"good" + 0.026*"place" + 0.015*"great" + 0.009*"service" + 0.008*"time" + 0.006*"price" + 0.006*"meal" + 0.006*"shop" + 0.006*"coffee"'), (9, '0.020*"food" + 0.014*"place" + 0.011*"meat" + 0.010*"line" + 0.009*"good" + 0.009*"minute" + 0.008*"time" + 0.008*"chicken" + 0.008*"wing" + 0.007*"hour"')] ------------------------------

Visualización PyLDAvis

