Sesgo y curtosis en la programación R

En estadística, la asimetría y la curtosis son las medidas que informan sobre la forma de la distribución de datos o, simplemente, ambos son métodos numéricos para analizar la forma del conjunto de datos, a diferencia de los gráficos e histogramas, que son métodos gráficos. Son pruebas de normalidad para comprobar la irregularidad y asimetría de la distribución. Para calcular la asimetría y la curtosis en lenguaje R, se requiere el paquete de momentos .

Oblicuidad

La asimetría es un método numérico estadístico para medir la asimetría de la distribución o conjunto de datos. Informa sobre la posición de la mayoría de los valores de los datos en la distribución alrededor del valor medio.
Fórmula: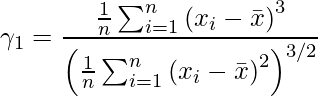
$\gamma_{1}=\frac{\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{3}}{\left(\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\right)^{3 / 2}}$
donde,

$\gamma_{1} $ representa el coeficiente de asimetría
$x_{i} $ representa el $i^\text{th}$ valor en el vector de datos
$\bar{x} $ representa la media del vector de datos
n representa el número total de observaciones

Existen 3 tipos de valores de asimetría sobre la base de los cuales se decide la asimetría del gráfico. Estos son los siguientes:

Sesgo positivo

Si el coeficiente de asimetría es mayor que 0, es decir $\gamma_{1}>0$ , se dice que el gráfico tiene una asimetría positiva con la mayoría de los valores de los datos inferiores a la media. La mayoría de los valores se concentran en el lado izquierdo del gráfico.
Ejemplo:

Python3

# Required for skewness() function
library(moments)
 
# Defining data vector
x <- c(40, 41, 42, 43, 50)
 
# output to be present as PNG file
png(file = "positiveskew.png")
 
# Print skewness of distribution
print(skewness(x))
 
# Histogram of distribution
hist(x)
 
# Saving the file
dev.off()

Producción:

[1] 1.2099

Representación grafica:

Asimetría cero o simétrica

Si el coeficiente de asimetría es igual a 0 o aproximadamente cercano a 0, es decir $\gamma_{1}=0$ , se dice que el gráfico es simétrico y que los datos se distribuyen normalmente.
Ejemplo:

Python3

# Required for skewness() function
library(moments)
 
# Defining normally distributed data vector
x <- rnorm(50, 10, 10)
 
# output to be present as PNG file
png(file = "zeroskewness.png")
 
# Print skewness of distribution
print(skewness(x))
 
# Histogram of distribution
hist(x)
 
# Saving the file
dev.off()

Producción:

[1] -0.02991511

Representación grafica:

sesgado negativamente

Si el coeficiente de asimetría es menor que 0, es decir $\gamma_{1}<0$ , entonces se dice que el gráfico tiene una asimetría negativa con la mayoría de los valores de los datos mayores que la media. La mayoría de los valores se concentran en el lado derecho del gráfico.
Ejemplo:

Python3

# Required for skewness() function
library(moments)
 
# Defining data vector
x <- c(10, 11, 21, 22, 23, 25)
 
# output to be present as PNG file
png(file = "negativeskew.png")
 
# Print skewness of distribution
print(skewness(x))
 
# Histogram of distribution
hist(x)
 
# Saving the file
dev.off()

Producción:

[1] -0.5794294

Representación grafica:

curtosis

La curtosis es un método numérico en estadística que mide la nitidez del pico en la distribución de datos.
Fórmula: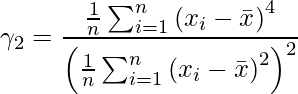
$\gamma_{2}=\frac{\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{4}}{\left(\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\right)^{2}}$
donde,

$\gamma_{2} $ representa el coeficiente de curtosis
$x_{i} $ representa el $i^\text{th}$ valor en el vector de datos
$\bar{x} $ representa la media del vector de datos
n representa el número total de observaciones

Existen 3 tipos de valores de curtosis sobre la base de los cuales se mide la nitidez del pico. Estos son los siguientes:

platicúrtico

Si el coeficiente de curtosis es inferior a 3, es decir $\gamma_{2}<3$ , la distribución de datos es platicúrtica. Ser platykurtic no significa que el gráfico sea plano.
Ejemplo:

Python3

# Required for kurtosis() function
library(moments)
 
# Defining data vector
x <- c(rep(61, each = 10), rep(64, each = 18),
rep(65, each = 23), rep(67, each = 32), rep(70, each = 27),
rep(73, each = 17))
 
# output to be present as PNG file
png(file = "platykurtic.png")
 
# Print skewness of distribution
print(kurtosis(x))
 
# Histogram of distribution
hist(x)
 
# Saving the file
dev.off()

Producción:

[1] 2.258318

Representación grafica:

mesocúrtico

Si el coeficiente de curtosis es igual a 3 o aproximadamente cercano a 3, es decir $\gamma_{2}=3$ , entonces la distribución de datos es mesocúrtica. Para una distribución normal, el valor de la curtosis es aproximadamente igual a 3.
Ejemplo:

Python3

# Required for kurtosis() function
library(moments)
 
# Defining data vector
x <- rnorm(100)
 
# output to be present as PNG file
png(file = "mesokurtic.png")
 
# Print skewness of distribution
print(kurtosis(x))
 
# Histogram of distribution
hist(x)
 
# Saving the file
dev.off()

Producción:

[1] 2.963836

Representación grafica:

leptocúrtico

Si el coeficiente de curtosis es mayor que 3, es decir $\gamma_{1}>3$ , la distribución de datos es leptocúrtica y muestra un pico pronunciado en el gráfico.
Ejemplo:

Python3

# Required for kurtosis() function
library(moments)
 
# Defining data vector
x <- c(rep(61, each = 2), rep(64, each = 5),
rep(65, each = 42), rep(67, each = 12), rep(70, each = 10))
 
# output to be present as PNG file
png(file = "leptokurtic.png")
 
# Print skewness of distribution
print(kurtosis(x))
 
# Histogram of distribution
hist(x)
 
# Saving the file
dev.off()

Producción:

[1] 3.696788

Representación grafica:

Publicación traducida automáticamente

Artículo escrito por utkarsh_kumar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Oblicuidad

Sesgo positivo

Python3

Asimetría cero o simétrica

Python3

sesgado negativamente

Python3

curtosis

platicúrtico

Python3

mesocúrtico

Python3

leptocúrtico

Python3

Deja una respuesta Cancelar la respuesta