Prerrequisito: Algoritmo de Diffie-Hellman
El algoritmo de intercambio de claves Diffie-Hellman es un método criptográfico avanzado que se utiliza para establecer un secreto compartido (o una clave secreta compartida) que se puede utilizar para realizar comunicaciones secretas en una red pública entre Alice y Bob mientras evita que Eve (escuchando a escondidas), que puede espiar toda su comunicación, desde el conocimiento del secreto generado.
El procedimiento de intercambio de claves consta de dos pasos:
- Configuración única: definimos algunos parámetros públicos que todos usarán para siempre.
- Protocolo: para generar nuevas claves secretas, ejecute un protocolo de intercambio de claves de dos mensajes. Este proceso se realiza usando algo de álgebra simple, números primos y propiedades de la aritmética modular.
Amenaza de seguridad del Diffie-Hellman
Supongamos que EVE, quien escucha a escondidas, conoce los valores públicos p y g como todos los demás, y de sus escuchas, también aprende los valores intercambiados por Alice y Bob, gᵃ mod p y gᵇ mod p. Con todo su conocimiento, todavía no puede calcular la clave secreta S, y resulta que si p y g se eligen correctamente, es muy, muy difícil para ella.
Por ejemplo, podría usar la fuerza bruta y probar todas las opciones, pero los cálculos (mod p) hacen que el cálculo del logaritmo discreto sea muy lento cuando los números son grandes. Si p y g tienen miles de bits, entonces los algoritmos más conocidos para calcular registros discretos, aunque sean más rápidos que la simple fuerza bruta, tardarán millones de años en calcularse.
Incluso con su inmunidad a la fuerza bruta, es vulnerable a MITM (hombre en la posición intermedia).
Man in the Middle (MITM) contra Diffie-Hellman:
Un Malory malicioso, que tiene una posición de MitM (hombre en el medio), puede manipular las comunicaciones entre Alice y Bob y romper la seguridad del intercambio de claves.
Explicación paso a paso de este proceso:
Paso 1: Números públicos seleccionados p y g, p es un número primo, llamado «módulo» y g se llama la base.
Paso 2: Selección de números privados.
deja que Alice elija un número aleatorio privado a y deja que Bob elija un número aleatorio privado b, Malory elige 2 números aleatorios c y d.
Paso 3: interceptar los valores públicos,
Malory intercepta el valor público de Alice (g a (mod p)), lo bloquea para que no llegue a Bob y, en su lugar, envía a Bob su propio valor público (g c (modp)) y Malory intercepta el valor público de Bob (g b (mod p)), bloquearlo para que no llegue a Alice y, en su lugar, enviar a Alice su propio valor público (g d (modp))
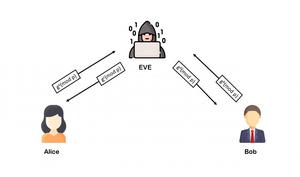
Paso 4: Cómputo de la clave secreta
Alice calculará una clave S 1 =g da (mod p), y Bob calculará una clave diferente, S 2 =g cb (mod p)
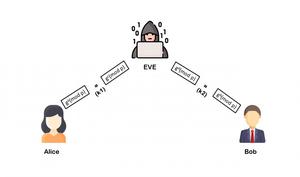
Paso 5: si Alice usa S 1 como clave para cifrar un mensaje posterior a Bob, Malory puede descifrarlo, volver a cifrarlo usando S 2 y enviárselo a Bob. Bob y Alice no notarán ningún problema y pueden suponer que su comunicación está cifrada, pero en realidad, Malory puede descifrar, leer, modificar y luego volver a cifrar todas sus conversaciones.
A continuación se muestra la implementación:
Python3
import random
# public keys are taken
# p is a prime number
# g is a primitive root of p
p = int(input('Enter a prime number : '))
g = int(input('Enter a number : '))
class A:
def __init__(self):
# Generating a random private number selected by alice
self.n = random.randint(1, p)
def publish(self):
# generating public values
return (g**self.n)%p
def compute_secret(self, gb):
# computing secret key
return (gb**self.n)%p
class B:
def __init__(self):
# Generating a random private number selected for alice
self.a = random.randint(1, p)
# Generating a random private number selected for bob
self.b = random.randint(1, p)
self.arr = [self.a,self.b]
def publish(self, i):
# generating public values
return (g**self.arr[i])%p
def compute_secret(self, ga, i):
# computing secret key
return (ga**self.arr[i])%p
alice = A()
bob = A()
eve = B()
# Printing out the private selected number by Alice and Bob
print(f'Alice selected (a) : {alice.n}')
print(f'Bob selected (b) : {bob.n}')
print(f'Eve selected private number for Alice (c) : {eve.a}')
print(f'Eve selected private number for Bob (d) : {eve.b}')
# Generating public values
ga = alice.publish()
gb = bob.publish()
gea = eve.publish(0)
geb = eve.publish(1)
print(f'Alice published (ga): {ga}')
print(f'Bob published (gb): {gb}')
print(f'Eve published value for Alice (gc): {gea}')
print(f'Eve published value for Bob (gd): {geb}')
# Computing the secret key
sa = alice.compute_secret(gea)
sea = eve.compute_secret(ga,0)
sb = bob.compute_secret(geb)
seb = eve.compute_secret(gb,1)
print(f'Alice computed (S1) : {sa}')
print(f'Eve computed key for Alice (S1) : {sea}')
print(f'Bob computed (S2) : {sb}')
print(f'Eve computed key for Bob (S2) : {seb}')
Producción:
Enter a prime number (p) : 227 Enter a number (g) : 14 Alice selected (a) : 227 Bob selected (b) : 170 Eve selected private number for Alice (c) : 65 Eve selected private number for Bob (d) : 175 Alice published (ga): 14 Bob published (gb): 101 Eve published value for Alice (gc): 41 Eve published value for Bob (gd): 32 Alice computed (S1) : 41 Eve computed key for Alice (S1) : 41 Bob computed (S2) : 167 Eve computed key for Bob (S2) : 167
Publicación traducida automáticamente
Artículo escrito por theellipsis009 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA