Requisito previo: dependencias funcionales
El término axiomas de Armstrong se refiere al conjunto sólido y completo de reglas de inferencia o axiomas, introducido por William W. Armstrong, que se utiliza para probar la implicación lógica de las dependencias funcionales . Si F es un conjunto de dependencias funcionales, entonces el cierre de F, denotado como ![]() , es el conjunto de todas las dependencias funcionales implicadas lógicamente por F. Los axiomas de Armstrong son un conjunto de reglas que, cuando se aplican repetidamente, generan un cierre de dependencias funcionales.
, es el conjunto de todas las dependencias funcionales implicadas lógicamente por F. Los axiomas de Armstrong son un conjunto de reglas que, cuando se aplican repetidamente, generan un cierre de dependencias funcionales.
axiomas –
- Axioma de reflexividad:
si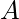 es un conjunto de atributos y
es un conjunto de atributos y 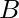 es un subconjunto de
es un subconjunto de 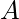 , entonces se
, entonces se 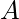 cumple
cumple 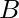 . Si
. Si 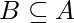 entonces
entonces 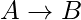 Esta propiedad es una propiedad trivial.
Esta propiedad es una propiedad trivial. - Axioma de aumento:
si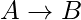 se cumple y
se cumple y 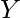 tiene un conjunto de atributos,
tiene un conjunto de atributos, 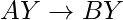 también se cumple. Eso es agregar atributos en las dependencias, no cambia las dependencias básicas. Si
también se cumple. Eso es agregar atributos en las dependencias, no cambia las dependencias básicas. Si 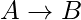 , entonces
, entonces 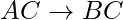 para cualquiera
para cualquiera  .
. - Axioma de transitividad:
igual que la regla transitiva en álgebra, si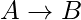 se cumple y
se cumple y 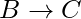 se cumple, entonces
se cumple, entonces  también se cumple.
también se cumple. 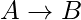 Se llama
Se llama 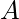 funcionalmente lo que determina
funcionalmente lo que determina 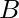 . Si
. Si 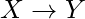 y
y 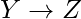 , entonces
, entonces 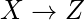
Reglas Secundarias –
Estas reglas se pueden derivar de los axiomas anteriores.
- Unión:
si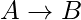 se mantiene y
se mantiene y  se mantiene, entonces se
se mantiene, entonces se  mantiene. si
mantiene. si 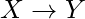 y
y 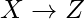 entonces
entonces 
- Composición:
si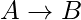 y
y 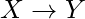 se mantiene, entonces se
se mantiene, entonces se 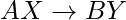 mantiene.
mantiene. - Descomposición:
si se mantiene, entonces
se mantiene, entonces 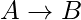 y se
y se  mantiene. Si
mantiene. Si 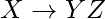 entonces
entonces 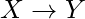 y
y 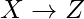
- Pseudo transitividad:
si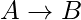 se mantiene y
se mantiene y  se mantiene, entonces se
se mantiene, entonces se 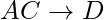 mantiene. Si
mantiene. Si 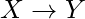 y
y 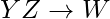 entonces
entonces  .
.
¿Por qué los axiomas de armstrong se refieren al sonido y completo?
Por sonido, queremos decir que dado un conjunto de dependencias funcionales F especificadas en un esquema de relación R, cualquier dependencia que podamos inferir de F usando las reglas primarias de los axiomas de Armstrong se cumple en cada estado de relación r de R que satisface las dependencias en F Por completo
, queremos decir que el uso repetido de las reglas primarias de los axiomas de Armstrong para inferir dependencias hasta que no se puedan inferir más dependencias da como resultado el conjunto completo de todas las dependencias posibles que se pueden inferir de F.
Referencias –
Este artículo es una contribución de Samit Mandal . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA