Banca de fórmula vial – Barcelona Geeks

Para un vehículo que va a gran velocidad por una carretera con curvas, la solución ideal es la peralte de la carretera. El borde exterior de una carretera se empuja hacia arriba durante una curva, haciéndolo más alto que el borde interior, y la superficie de la carretera se asemeja a un plano ligeramente inclinado para la seguridad del vehículo. Este proceso se conoce como peralte de carreteras o peralte de carreteras.

En otras palabras, peralte de carretera se refiere a la técnica de levantar el borde exterior (borde) de una carretera por encima de su borde interior (borde) en un ángulo específico (el ángulo aquí se conoce como ángulo de peralte).

Necesidad de peralte de la carretera

Cuando el vehículo se desplaza por una carretera con curvas, se debe proporcionar la fuerza centrípeta, de lo contrario, existe el peligro de que el vehículo salga disparado tangencialmente.
La fuerza de fricción entre las ruedas y el camino puede generar una fuerza centrípeta, pero la velocidad segura para tales caminos es muy baja y no es confiable.
En el peralte de carreteras, la componente horizontal de reacción normal proporciona la fuerza centrípeta necesaria, y los vehículos quedan protegidos de accidentes.

Fórmulas relacionadas con peraltes de carreteras

La velocidad de un vehículo en una carretera peraltada curva: v = $\sqrt{(\frac{Rg(μs + tanθ)}{(1−μs tanθ)}}$

Para un par de caminos dado, y Tire μ _s = tanλ, entonces la velocidad de un vehículo en un camino con peralte curvo es: v = $\sqrt{Rg tan(θ + λ)}$

La velocidad segura en una carretera sin peralte es: v _max = $\sqrt{μ Rg}$

La expresión para el ángulo de peralte de la carretera es: θ = tan ^-1 [v ₀² / Rg]

La expresión para la velocidad segura en el camino peraltado es: v _max = $\sqrt{rg tanθ}$

La derivación para todas las fórmulas se da a continuación,

Derivaciones

Considere la figura anterior, donde

mg = peso del vehículo

N = reacción normal

f = fuerza de fricción

f cosθ = componente horizontal de la fuerza de fricción

f sinθ = componente vertical de la fuerza de fricción

N cosθ = componente vertical de la reacción normal

N sinθ = componente horizontal de la reacción normal

Considere un vehículo de masa m que se mueve con velocidad v a lo largo de una carretera peraltada curva que forma un ángulo θ . Sea f la fuerza de fricción entre las llantas del vehículo y la superficie de la carretera.

Las fuerzas que actúan sobre el vehículo son,

Peso mg actuando verticalmente hacia abajo
Reacción normal N en reacción ascendente a través del centro de gravedad y perpendicular a la carretera/superficie peraltada.

La fuerza de fricción entre los neumáticos del vehículo y la superficie de la carretera se puede descomponer en,

f cosθ – a lo largo de la dirección horizontal
f sinθ – a lo largo de una dirección vertical hacia abajo

La reacción normal se puede resolver en dos componentes,

N cosθ – Componente vertical de reacción normal
N sinθ – Componente horizontal de reacción normal

El componente N cosθ de la reacción normal se equilibra con el peso mg del vehículo y el componente f sinθ de la fuerza de fricción,

N cosθ = mg + f senθ

∴ mg = N cosθ – f senθ ⇢ (1)

La componente horizontal N senθ junto con la componente f cosθ de la fuerza de fricción proporciona la fuerza centrípeta necesaria.

norte senθ + f cosθ = mv ² / R

O, mv ² / R = N senθ + f cosθ ⇢ (2)

Dividiendo la ecuación (2) por la ecuación (1),

v ² / Rg = N senθ + f cosθ / N cosθ – f senθ ⇢ (3)

La magnitud de la fuerza de fricción depende de la velocidad del vehículo para una superficie de carretera determinada y de los neumáticos del vehículo. Sea v _max la velocidad máxima del vehículo, la fuerza de fricción f _m producida a esta velocidad debe ser

F _metro = μ _s norte ⇢ (4)

v ²_máx / Rg = N senθ + f cosθ / N cosθ – f senθ ⇢ (5)

De la ecuación (4) y la ecuación (5), obtenemos v _max

∴ v _máx = $\sqrt{\frac{Rg[( μs + tanθ)}{(1 - μs tanθ) ]}}$ ⇢ (6)

Para un camino horizontal curvo, θ = 0°, por lo tanto, la ecuación (6) se convierte en,

v _máx = √{μ Rg} ⇢ (7)

Ahora, si comparamos la ecuación (6) y la ecuación (7), se revela que la velocidad máxima segura de los vehículos en una carretera peraltada es mayor que la de una carretera curva horizontal/carretera nivelada.

Si μ _s = 0, entonces la ecuación (6) se convierte en

v _máx = v ₀ = $\sqrt{\frac{Rg (0 + tanθ)}{1 - 0 tanθ }}$

v ₀ = $\sqrt{Rg tanθ}$ ⇢ (8)

A esta velocidad, la fuerza de fricción no es necesaria para proporcionar la fuerza centrípeta necesaria. habrá un poco de agua y se rasgará el neumático si se conduce el vehículo a esta velocidad en una carretera con peralte. v ₀ se llama velocidad óptima.

De la ecuación (8), es decir

v ₀ = $\sqrt{Rg tanθ}$

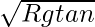
tanθ = v ₀² / Rg

θ = tan ^-1 [v ₀² / Rg] ⇢ (9)

Nota : Esta fórmula [Eq (9)] para el ángulo de inclinación lateral no involucra la masa del vehículo m. Así, el ángulo de inclinación es independiente de la masa del vehículo.

Problemas de muestra

Pregunta 1: encuentre la velocidad máxima de un automóvil con la que se puede conducir con seguridad a lo largo de una curva de 100 m de radio y el coeficiente de fricción entre las llantas y la carretera es 0.2. (Tome g = 9,8 m/s ² )

Solución:

Datos dados:

Radio (r) = 100m

Coeficiente de fricción (μ) = 0,2

Gravedad (g) = 9,8 m/s ²

Fórmula: v= √(μrg)

v = √(μrg)

= √(0,2 × 100 × 9,8)

= √196

v = 14 m/s

Por lo tanto, la velocidad máxima del automóvil es de 14 m/s.

Pregunta 2: Calcular la velocidad máxima con la que un automóvil puede ser conducido con seguridad a lo largo de una carretera con curvas de un radio de 30 m y peralte en un ángulo de 30 ° con la horizontal. (toma g = 9,8 m/s ² )

Datos dados:

Radio (r) = 30m

Ángulo de peralte de la carretera (θ) = 30°

Gravedad (g) = 9,8 m/s ²

Fórmula: v= √rg tanθ

v= $\sqrt{rg tanθ}$

= $\sqrt{30 × 9.8 × tan 30° }$

= $\sqrt{30 × 9.8 × 0.5774}$

v = 13,03 m/s

Por tanto, la velocidad máxima del coche es de 13,03 m/s

Pregunta 3: Halla el ángulo que forman la bicicleta y su ciclista con la vertical cuando van a 18 km/h por una carretera curva de 10 m de radio en terreno llano. (Tome g = 9,8 m/s ² )

Datos dados:

Radio (r) = 10 m

Velocidad máxima del ciclista (v) = 18 km/h

Gravedad (g) = 9,8 m/s ²

Fórmula: tanθ = v ² / rg

v = 18 km/h

= 18 × 1000 / 3600

= 5 m/s

El ángulo tangente de peralte es tanθ = v ² / rg

= 5 × 5 / 10 × 9,8

= 5 / 2 × 9,8

tanθ = 0.251

θ = bronceado ^-1 (0,2551)

θ = 14 ° 19 ^‘

Por lo tanto, el ángulo que forman la bicicleta y el ciclista es de 14 ° 19 ^‘

Pregunta 4: Una camioneta de motor que pesa 4400 kg toma una curva nivelada de 200 m de radio en una carretera sin peralte a 60 km/h. ¿Cuál debe ser el valor mínimo del coeficiente de fricción para evitar el deslizamiento? ¿A qué ángulo debe inclinarse el camino para esta velocidad?

Datos dados:

Peso de la furgoneta (m) = 4400 kg

Radio (r) = 200m

Velocidad de la furgoneta (v) = 60 km/h

Gravedad (g) = 9,8 m/s ²

v = 60 km/h

= 60 × 1000 / 3600

= 50 / 3 m/s

Para evitar el derrape, mv ² / r = μmg

μ = v ² / rg

= (50 / 3) ² / 200 × 9,8

= 25 / 18 × 9,8

µ = 0,1417

Ángulo de inclinación tanθ es = v ² / rg

= (50 / 3) ² / 200 × 9,8

tanθ = 0.1417

θ = bronceado ^-1 (0,1417)

θ = 8 ° 4 ^‘

Así, el coeficiente de fricción es 0,1417 y el ángulo de inclinación lateral es 8 ° 4 ^‘ .

Pregunta 5: La pista de un hipódromo circular tiene un radio de 500 m y está inclinada a 100. Si el coeficiente de fricción entre las llantas del vehículo y la superficie de la carretera es 0.25. Calcule la velocidad máxima para evitar el deslizamiento del automóvil y la velocidad óptima para evitar el desgaste de las llantas. (Tome g = 9,8 m/s ² )

Datos dados:

Radio (r) = 500m

Ángulo (θ) = 10°

Coeficiente de Fricción (μ) = 0.25

ya que, θ = 10°

tan10° = 0.1763

En la pista peraltada, la velocidad máxima para evitar resbalones,

v _máx = $\sqrt{(\frac{Rg(μs + tanθ)}{(1−μs tanθ)}}$

= $\sqrt{\frac{500 × 9.8(0.25 + 0.1763)}{(1 - (0.25 × 0.1763))}}$

= √{500 × 9,8 × 0,4263 / 0,9559}

= √2185

vmáx = _46,75 m/s

La velocidad óptima del vehículo en la vía viene dada por v _opt = $\sqrt{rg tanθ}$

= $\sqrt{500 × 9.8 × 0.1763}$

= √863.9

v _opt = 29,39 m/s

Pregunta 6: Encuentra el ángulo de peralte de la vía férrea con un radio de curvatura de 1500m. Si la velocidad máxima del tren es de 15 m/s. Si la distancia entre las dos vías es de 1,8 m, calcule la elevación de la vía exterior sobre la vía interior.

Datos dados:

Radio (r) = 1500m

Velocidad (v) = 15 m/s

Distancia entre dos pistas (l) = 1,8 m

Ángulo tangente de Banca,

tanθ = v ² / rg

= 15 × 15 / 1500 × 9,8

= 0.015306

θ = bronceado ^-1 (0,0153)

θ = 0° 52′

Considere la figura anterior,

senθ = h / l

h = l × senθ

= 1.8 × sen(0° 52′)

= 1,8 × 0,0157

h = 0.02826

El ángulo de peralte es de 0° 52′ y la elevación de la vía exterior sobre la vía interior es de 0,02826.

Pregunta 7: Un tren de vía métrica se mueve a 60 km/h a lo largo de una carretera con curvas de un radio de curvatura de 500 m en cierto lugar. Encuentre la elevación del riel exterior sobre el riel interior, de modo que no haya presión lateral sobre el riel (tome g = 9,8 m/s ² )

Datos dados:

Velocidad (v) = 60Km/Hr = 50 / 3 m/s

Radio (r) = 500m

l = 1m

En caso de vía férrea peraltada,

tanθ = v ² / rg

= (50 / 3 ) ² / 500 × 9,8

= 0.05670

θ = bronceado ^-1 (0.05670)

θ = 3° 15′

Elevación del riel exterior sobre el riel interior,

h = l senθ

= (1) sen(3° 15′)

h = 0,0567m

Publicación traducida automáticamente

Artículo escrito por lunaticgemini2510 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Fórmulas relacionadas con peraltes de carreteras

Problemas de muestra

Deja una respuesta Cancelar la respuesta