BFS vs DFS para árbol binario

¿Qué son BFS y DFS para Binary Tree? Por lo general, un árbol se recorre de dos maneras:

• Recorrido de ancho primero (o recorrido de orden de nivel)
• Primeros recorridos de profundidad
  • Recorrido en orden (izquierda-raíz-derecha)
  • Recorrido de pedido anticipado (Raíz-Izquierda-Derecha)
  • Recorrido posorden (raíz izquierda-derecha)

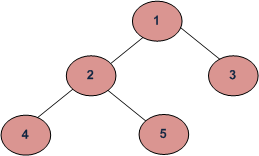
BFS and DFSs of above Tree

Breadth First Traversal : 1 2 3 4 5 or 1 2 3 5 4 or 1 3 2 4 5 or 1 3 2 5 4 

Depth First Traversals: 
      Preorder Traversal : 1 2 4 5 3 
      Inorder Traversal  :  4 2 5 1 3 
      Postorder Traversal : 4 5 2 3 1

¿Por qué nos importa? Hay muchas preguntas de árboles que se pueden resolver usando cualquiera de los cuatro recorridos anteriores. Ejemplos de tales preguntas son tamaño , máximo , mínimo , vista izquierda de impresión , etc. ¿Hay alguna diferencia en términos de Complejidad de tiempo? Los cuatro recorridos requieren tiempo O(n) ya que visitan cada Node exactamente una vez. ¿Hay alguna diferencia en términos de Espacio Extra? Hay diferencia en términos de espacio extra requerido.

1. El espacio adicional requerido para el recorrido de orden de nivel es O(w), donde w es el ancho máximo del árbol binario. En el recorrido de orden de nivel, la cola uno por uno almacena Nodes de diferente nivel.
2. El espacio adicional necesario para los primeros recorridos en profundidad es O(h), donde h es la altura máxima del árbol binario. En Depth First Traversals, la pila (o pila de llamadas de función) almacena todos los ancestros de un Node.

El ancho máximo de un árbol binario en la profundidad (o altura) h puede ser 2 ^h donde h comienza desde 0. Por lo tanto, el número máximo de Nodes puede estar en el último nivel. Y el peor de los casos ocurre cuando el árbol binario es un árbol binario perfecto con números de Nodes como 1, 3, 7, 15, etc. En el peor de los casos, el valor de 2 ^h es Ceil(n/2) . La altura de un árbol binario equilibrado es O (Log n). El peor de los casos ocurre para el árbol sesgado y la altura del peor de los casos se convierte en O(n). Entonces, en el peor de los casos, el espacio adicional requerido es O (n) para ambos. Pero los peores casos ocurren para diferentes tipos de árboles. Es evidente a partir de los puntos anteriores que es probable que el espacio adicional requerido para el recorrido de orden de nivel sea mayor cuando el árbol está más equilibrado y que el espacio adicional para el recorrido primero en profundidad es probable que sea mayor cuando el árbol está menos equilibrado. ¿Cómo elegir uno?

1. El espacio adicional puede ser un factor (explicado anteriormente)
2. Los primeros recorridos en profundidad suelen ser recursivos y el código recursivo requiere gastos generales de llamadas a funciones.
3. Los puntos más importantes son que BFS comienza a visitar los Nodes desde la raíz, mientras que DFS comienza a visitar los Nodes desde las hojas. Entonces, si nuestro problema es buscar algo que tenga más probabilidades de estar más cerca de la raíz, preferiríamos BFS. Y si el Node de destino está cerca de una hoja, preferiríamos DFS.

Ejercicio: ¿Qué recorrido se debe usar para imprimir hojas de Binary Tree y por qué? ¿Qué recorrido se debe usar para imprimir Nodes en el k-ésimo nivel donde k es mucho menor que el número total de niveles? Este artículo es una contribución de Dheeraj Gupta . Esto Por favor escriba comentarios si encuentra algo incorrecto, o si desea compartir más información sobre el tema discutido anteriormente