BK Tree o Burkhard Keller Tree es una estructura de datos que se utiliza para realizar la revisión ortográfica basada en el concepto de distancia de edición (distancia de Levenshtein). Los árboles BK también se utilizan para la coincidencia aproximada de strings. Se pueden implementar varias funciones de corrección automática en muchos programas en función de esta estructura de datos.
Pre-requisites : Edit distance Problem Metric tree
Digamos que tenemos un diccionario de palabras y luego tenemos algunas otras palabras que deben revisarse en el diccionario para detectar errores ortográficos. Necesitamos tener una colección de todas las palabras en el diccionario que estén muy cerca de la palabra dada. Por ejemplo, si estamos marcando una palabra “ ruk ”, tendremos {“truck”,”buck”,”duck”,……} . Por lo tanto, el error de ortografía se puede corregir eliminando un carácter de la palabra o agregando un nuevo carácter en la palabra o reemplazando el carácter en la palabra por uno apropiado. Por lo tanto, utilizaremos la distancia de edición como una medida de corrección y coincidencia de la palabra mal escrita de las palabras de nuestro diccionario.
Ahora, veamos la estructura de nuestro árbol BK. Como todos los demás árboles, BK Tree consta de Nodes y aristas. Los Nodes en el Árbol BK representarán las palabras individuales en nuestro diccionario y habrá exactamente el mismo número de Nodes que el número de palabras en nuestro diccionario. El borde contendrá algún peso entero que nos informará sobre la distancia de edición de un Node a otro. Digamos que tenemos un borde desde el Node u hasta el Node v que tiene un peso de borde w , entonces w es la distancia de edición requerida para convertir la string u en v.
Considere nuestro diccionario con palabras: { «ayuda», «infierno», «hola»} . Por lo tanto, para este diccionario, nuestro árbol BK se verá como el siguiente.

Cada Node en el árbol BK tendrá exactamente un hijo con la misma distancia de edición. En caso de que encontremos alguna colisión en la distancia de edición durante la inserción, propagaremos el proceso de inserción a los elementos secundarios hasta que encontremos un elemento principal apropiado para el Node de string.
Cada inserción en el árbol BK comenzará desde nuestro Node raíz. El Node raíz puede ser cualquier palabra de nuestro diccionario.
Por ejemplo, agreguemos otra palabra » shell » al diccionario anterior. Ahora nuestro Dict[] = {“ayuda”, “infierno”, “hola”, “cáscara”} . Ahora es evidente que » shell » tiene la misma distancia de edición que » hello » desde el Node raíz » help «, es decir, 2. Por lo tanto, nos encontramos con una colisión. Por lo tanto, tratamos esta colisión haciendo recursivamente este proceso de inserción en el Node de colisión preexistente.
Entonces, ahora en lugar de insertar » shell » en el Node raíz » ayuda «, ahora lo insertaremos en el Node en colisión » hola“. Por lo tanto, ahora el nuevo Node » shell » se agrega al árbol y tiene el Node » hello » como su padre con el peso de borde de 2 (editar-distancia). A continuación, la representación pictórica describe el árbol BK después de esta inserción.
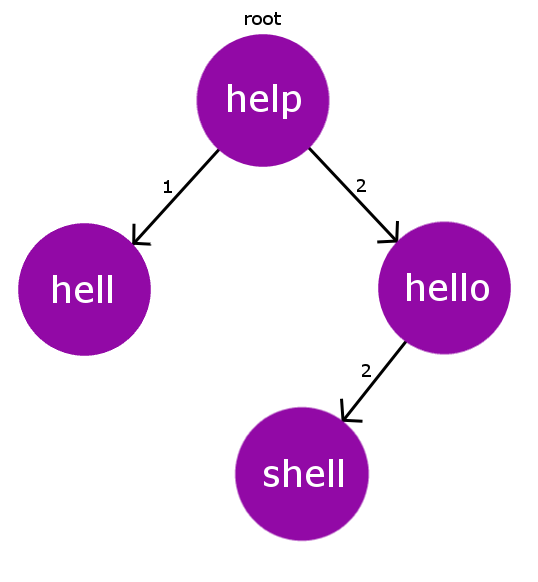
Entonces, hasta ahora hemos entendido cómo construiremos nuestro Árbol BK. Ahora, surge la pregunta de cómo encontrar la palabra correcta más cercana a nuestra palabra mal escrita. En primer lugar, debemos establecer un valor de tolerancia. Este valor de tolerancia es simplemente la distancia máxima de edición desde nuestra palabra mal escrita hasta las palabras correctas en nuestro diccionario. Entonces, para encontrar las palabras correctas elegibles dentro del límite de tolerancia, el enfoque ingenuo será iterar sobre todas las palabras en el diccionario y recopilar las palabras que están dentro del límite de tolerancia. Pero este enfoque tiene una complejidad de tiempo O(n*m*n) ( n es el número de palabras en dict[], m es el tamaño promedio de la palabra correcta y nes la longitud de la palabra mal escrita) que se agota para un diccionario de mayor tamaño.
Por lo tanto, ahora el Árbol BK entra en acción. Como sabemos, cada Node en BK Tree se construye sobre la base de la medida de distancia de edición de su padre. Por lo tanto, iremos directamente desde el Node raíz a Nodes específicos que se encuentran dentro del límite de tolerancia. Digamos que nuestro límite de tolerancia es TOL y la distancia de edición del Node actual desde la palabra mal escrita es dist . Por lo tanto, ahora, en lugar de iterar sobre todos sus hijos, solo iteraremos sobre sus hijos que tienen distancia de edición en el rango
[ dist-TOL , dist+TOL ]. Esto reducirá nuestra complejidad en gran medida. Discutiremos esto en nuestro análisis de la complejidad del tiempo.
Considere el árbol BK construido a continuación.
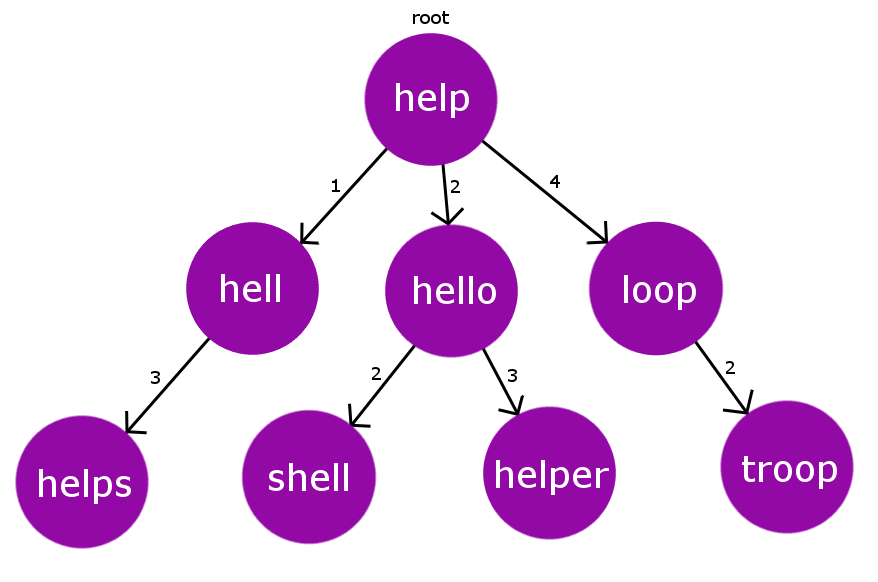
Digamos que tenemos una palabra mal escrita “ oop ” y el límite de tolerancia es 2. Ahora, veremos cómo recopilaremos la respuesta correcta esperada para la palabra mal escrita dada.
Iteración 1: Comenzaremos a verificar la distancia de edición desde el Node raíz. D(“oop” -> “ayuda”) = 3. Ahora vamos a iterar sobre sus elementos secundarios teniendo la distancia de edición en el rango [D-TOL, D+TOL], es decir, [1,5]
Iteración 2: empecemos a iterar desde el más alto posible editar distancia hijo, es decir, Node «bucle» con editar distancia 4. Ahora, una vez más, encontraremos su distancia de edición de nuestra palabra mal escrita. D(“oop”,”loop”) = 1.
aquí D = 1, es decir, D <= TOL, por lo que agregaremos “loop” a la lista de palabras correcta esperada y procesaremos sus Nodes secundarios con una distancia de edición en el rango [D-TOL ,D+TOL] es decir [1,3]
Iteración 3: Ahora, estamos en el Node «tropa». Una vez más, comprobaremos su distancia de edición desde la palabra mal escrita. D(“oop”,”tropa”)=2 .Aquí nuevamente D <= TOL , por lo tanto nuevamente agregaremos “tropa” a la lista de palabras correcta esperada.
Procederemos de la misma manera para todas las palabras del rango [D-TOL,D+TOL] comenzando desde el Node raíz hasta el Node hoja más inferior. Esto es similar a un recorrido DFS en un árbol, visitando selectivamente los Nodes secundarios cuyo peso de borde se encuentra en un rango determinado.
Por lo tanto, al final nos quedarán solo 2 palabras esperadas para la palabra mal escrita “ oop ”, es decir , {“bucle”, “tropa”}
C++
// C++ program to demonstrate working of BK-Tree
#include "bits/stdc++.h"
using namespace std;
// maximum number of words in dict[]
#define MAXN 100
// defines the tolerance value
#define TOL 2
// defines maximum length of a word
#define LEN 10
struct Node
{
// stores the word of the current Node
string word;
// links to other Node in the tree
int next[2*LEN];
// constructors
Node(string x):word(x)
{
// initializing next[i] = 0
for(int i=0; i<2*LEN; i++)
next[i] = 0;
}
Node() {}
};
// stores the root Node
Node RT;
// stores every Node of the tree
Node tree[MAXN];
// index for current Node of tree
int ptr;
int min(int a, int b, int c)
{
return min(a, min(b, c));
}
// Edit Distance
// Dynamic-Approach O(m*n)
int editDistance(string& a,string& b)
{
int m = a.length(), n = b.length();
int dp[m+1][n+1];
// filling base cases
for (int i=0; i<=m; i++)
dp[i][0] = i;
for (int j=0; j<=n; j++)
dp[0][j] = j;
// populating matrix using dp-approach
for (int i=1; i<=m; i++)
{
for (int j=1; j<=n; j++)
{
if (a[i-1] != b[j-1])
{
dp[i][j] = min( 1 + dp[i-1][j], // deletion
1 + dp[i][j-1], // insertion
1 + dp[i-1][j-1] // replacement
);
}
else
dp[i][j] = dp[i-1][j-1];
}
}
return dp[m][n];
}
// adds curr Node to the tree
void add(Node& root,Node& curr)
{
if (root.word == "" )
{
// if it is the first Node
// then make it the root Node
root = curr;
return;
}
// get its editDistance from the Root Node
int dist = editDistance(curr.word,root.word);
if (tree[root.next[dist]].word == "")
{
/* if no Node exists at this dist from root
* make it child of root Node*/
// incrementing the pointer for curr Node
ptr++;
// adding curr Node to the tree
tree[ptr] = curr;
// curr as child of root Node
root.next[dist] = ptr;
}
else
{
// recursively find the parent for curr Node
add(tree[root.next[dist]],curr);
}
}
vector <string> getSimilarWords(Node& root,string& s)
{
vector < string > ret;
if (root.word == "")
return ret;
// calculating editdistance of s from root
int dist = editDistance(root.word,s);
// if dist is less than tolerance value
// add it to similar words
if (dist <= TOL) ret.push_back(root.word);
// iterate over the string having tolerance
// in range (dist-TOL , dist+TOL)
int start = dist - TOL;
if (start < 0)
start = 1;
while (start <= dist + TOL)
{
vector <string> tmp =
getSimilarWords(tree[root.next[start]],s);
for (auto i : tmp)
ret.push_back(i);
start++;
}
return ret;
}
// driver program to run above functions
int main(int argc, char const *argv[])
{
// dictionary words
string dictionary[] = {"hell","help","shell","smell",
"fell","felt","oops","pop","oouch","halt"
};
ptr = 0;
int sz = sizeof(dictionary)/sizeof(string);
// adding dict[] words on to tree
for(int i=0; i<sz; i++)
{
Node tmp = Node(dictionary[i]);
add(RT,tmp);
}
string w1 = "ops";
string w2 = "helt";
vector < string > match = getSimilarWords(RT,w1);
cout << "similar words in dictionary for : " << w1 << ":\n";
for (auto x : match)
cout << x << endl;
match = getSimilarWords(RT,w2);
cout << "Correct words in dictionary for " << w2 << ":\n";
for (auto x : match)
cout << x << endl;
return 0;
}
similar words in dictionary for : ops: oops pop Correct words in dictionary for helt: hell help shell fell felt halt
Complejidad del tiempo: es bastante evidente que la complejidad del tiempo depende en gran medida del límite de tolerancia. Consideraremos que el límite de tolerancia es 2 . Ahora, estimando aproximadamente, la profundidad de BK Tree será log n, donde n es el tamaño del diccionario. En cada nivel, visitamos 2 Nodes en el árbol y realizamos el cálculo de la distancia de edición. Por lo tanto, nuestra Complejidad de tiempo será O(L1*L2*log n) , aquí L1 es la longitud promedio de la palabra en nuestro diccionario y L2 es la longitud de las palabras mal escritas. Generalmente, L1 y L2 serán pequeños.
Referencias
Este artículo es una contribución de Nitish Kumar . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA