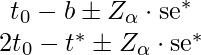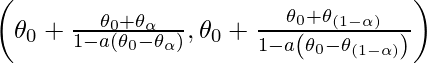Bootstrapping en Programación R

Bootstrapping es una técnica utilizada en estadísticas inferenciales que trabajan en la construcción de muestras aleatorias de conjuntos de datos únicos una y otra vez. Bootstrapping permite calcular medidas como media, mediana, moda, intervalos de confianza, etc. del muestreo.

R – Arranque automático

El siguiente es el proceso de arranque en lenguaje de programación R:

Seleccione el número de muestras de arranque.
Seleccione el tamaño de cada muestra.
Para cada muestra, si el tamaño de la muestra es menor que la muestra elegida, seleccione una observación aleatoria del conjunto de datos y agréguela a la muestra.
Mida la estadística en la muestra.
Mida la media de todos los valores de muestra calculados.

Métodos de arranque

Hay 2 métodos de arranque:

Remuestreo residual: este método también se denomina remuestreo basado en modelos. Este método asume que el modelo es correcto y que los errores son independientes y se distribuyen de manera idéntica. Después de cada remuestreo, las variables se redefinen y se utilizan nuevas variables para medir las nuevas variables dependientes.
Pares Bootstrap: en este método, las variables dependientes e independientes se usan juntas como pares para el muestreo.

Tipos de Intervalos de Confianza en Bootstrapping

El intervalo de confianza (IC) es un tipo de valor computacional calculado sobre datos de muestra en estadísticas. Produce un rango de valores o un intervalo donde el verdadero valor se encuentra con seguridad. Hay 5 tipos de intervalos de confianza en el arranque de la siguiente manera:

Básico: también se conoce como Intervalo de percentil inverso y se genera utilizando cuantiles de distribución de datos de arranque. Matemáticamente,

$\left(2 \widehat{\theta}-\theta_{(1-\alpha / 2)}^{*}, 2 \widehat{\theta}-\theta_{(\alpha / 2)}^{*}\right)$

donde,
$\alpha$ representa el intervalo de confianza, en su mayoría $\alpha = 0.95$
$\theta^{*}$ representa los coeficientes de bootstrap
$\theta_{(1-\alpha / 2)}^{*}$ representa el $1-\alpha / 2$ percentil de los coeficientes de bootstrapping

Normal: el IC normal se expresa matemáticamente como,

$\begin{array}{c} t_{0}-b \pm Z_{\alpha} \cdot \mathrm{se}^{*} \\ 2 t_{0}-t^{*} \pm Z_{\alpha} \cdot \mathrm{se}^{*} \end{array}$
dónde,

$t_{0}$ representa un valor del conjunto de datos t
b es el sesgo de la estimación de arranque, es decir,

$\mathbf{b}=\mathbf{t}^{*}-\mathbf{t}_{\mathrm{o}}$
$Z_{\alpha}$ representa el $1-\alpha / 2$ cuantil de la distribución bootstrap
$se^{*}$ representa el error estándar de $t^{*}$

Stud: En el IC estudentizado, los datos se normalizan con el centro en 0 y la desviación estándar en 1, corrigiendo el sesgo de distribución.
Perc : el IC percentil es similar al IC básico pero con una fórmula diferente,

$\left(\theta_{(\alpha / 2)}^{*}, \theta_{(1-\alpha / 2)}^{*}\right)$

BCa: este método se ajusta tanto al sesgo como al sesgo, pero puede ser inestable cuando los valores atípicos son extremos. Matemáticamente,

$\left(\theta_{0}+\frac{\theta_{0}+\theta_{\alpha}}{1-a\left(\theta_{0}-\theta_{\alpha}\right)}, \theta_{0}+\frac{\theta_{0}+\theta_{(1-\alpha)}}{1-a\left(\theta_{0}-\theta_{(1-\alpha)}\right)}\right)$

La sintaxis para realizar bootstrapping en programación R es la siguiente:

Sintaxis: boot(datos, estadística, R)

Parámetros:

los datos representan el conjunto de datos

statistic representa las funciones estadísticas que se realizarán en el conjunto de datos

R representa el número de muestras

Para conocer más argumentos opcionales de la función boot(), use el siguiente comando:

help("boot")

Ejemplo:

R

# Library required for boot() function
install.packages("boot")
 
# Load the library
library(boot)
 
# Creating a function to pass into boot() function
bootFunc <- function(data, i){
df <- data[i, ]
c(cor(df[, 2], df[, 3]),
    median(df[, 2]),
    mean(df[, 1])
)
}
 
b <- boot(mtcars, bootFunc, R = 100)
 
print(b)
 
# Show all CI values
boot.ci(b, index = 1)

Producción:

ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = mtcars, statistic = bootFunc, R = 100)


Bootstrap Statistics :
      original       bias    std. error
t1*  0.9020329 -0.002195625  0.02104139
t2*  6.0000000  0.340000000  0.85540468
t3* 20.0906250 -0.110812500  0.96052824


BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 100 bootstrap replicates

CALL : 
boot.ci(boot.out = b, index = 1)

Intervals : 
Level      Normal              Basic         
95%   ( 0.8592,  0.9375 )   ( 0.8612,  0.9507 )  

Level     Percentile            BCa          
95%   ( 0.8534,  0.9429 )   ( 0.8279,  0.9280 )  
Calculations and Intervals on Original Scale
Some basic intervals may be unstable
Some percentile intervals may be unstable
Warning : BCa Intervals used Extreme Quantiles
Some BCa intervals may be unstable
Warning messages:
1: In boot.ci(b, index = 1) :
  bootstrap variances needed for studentized intervals
2: In norm.inter(t, adj.alpha) :
  extreme order statistics used as endpoints

Publicación traducida automáticamente

Artículo escrito por utkarsh_kumar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

R – Arranque automático

El siguiente es el proceso de arranque en lenguaje de programación R:

Métodos de arranque

Tipos de Intervalos de Confianza en Bootstrapping

R

Deja una respuesta Cancelar la respuesta