Declaración del problema: dado un texto txt[0..n-1] y un patrón pat[0..m-1], escriba una función de búsqueda (char pat[], char txt[]) que imprima todas las apariciones de pat[ ] en texto[]. Puede suponer que n > m.
Como se discutió en la publicación anterior , discutimos que hay dos formas de resolver de manera eficiente el problema anterior.
1) Patrón de preproceso: algoritmo KMP , algoritmo Rabin Karp , autómatas finitos , algoritmo Boyer Moore .
2) Preprocesar texto: árbol de sufijos
La mejor complejidad de tiempo posible lograda por el primero (patrón de preprocesamiento) es O (n) y por el segundo (texto de preprocesamiento) es O (m) donde m y n son longitudes de patrón y texto respectivamente.
Tenga en cuenta que la segunda forma realiza la búsqueda solo en tiempo O(m) y se prefiere cuando el texto no cambia con mucha frecuencia y hay muchas consultas de búsqueda. Hemos discutido el Árbol de Sufijos (Un Trie comprimido de todos los sufijos de Texto) .
La implementación de Suffix Tree puede llevar mucho tiempo para que los problemas se codifiquen en una entrevista técnica o en contextos de programación. En esta publicación, se analiza la implementación simple de un Trie estándar de todos los sufijos. La implementación está cerca del árbol de sufijos, lo único es que es un Trie simple en lugar de un Trie comprimido.
Como se discutió en la publicación Suffix Tree , la idea es que cada patrón que está presente en el texto (o podemos decir cada substring de texto) debe ser un prefijo de uno de todos los sufijos posibles. Entonces, si construimos un Trie de todos los sufijos, podemos encontrar el patrón en el tiempo O(m) donde m es la longitud del patrón.
Construyendo un Trie de Sufijos
1) Genere todos los sufijos de un texto dado.
2) Considere todos los sufijos como palabras individuales y construya un trie.
Consideremos un texto de ejemplo “banana\0” donde ‘\0’ es un carácter de terminación de string. Los siguientes son todos los sufijos de “banana\0”
banana\0 anana\0 nana\0 ana\0 na\0 a\0 \0
Si consideramos todos los sufijos anteriores como palabras individuales y construimos un Trie, obtenemos seguimiento.
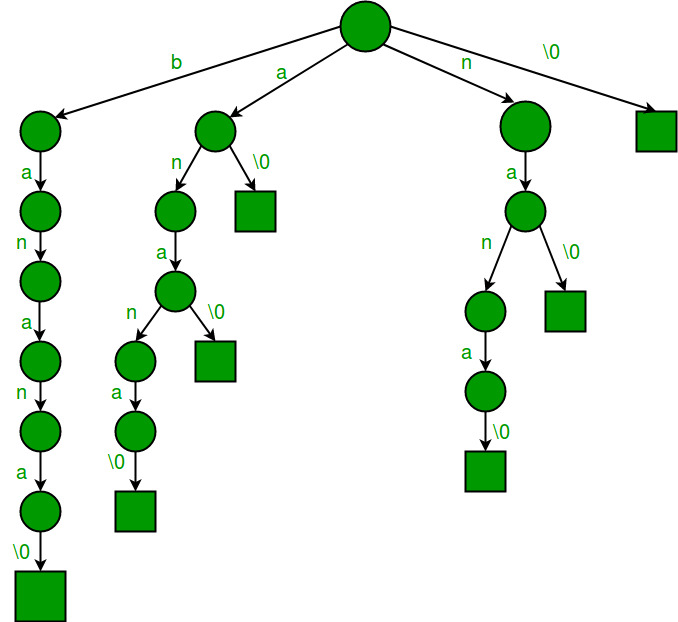
¿Cómo buscar un patrón en el Trie construido?
Los siguientes son pasos para buscar un patrón en el Trie construido.
1) Comenzando desde el primer carácter del patrón y la raíz del Trie, haga lo siguiente para cada carácter.
….. a) Para el carácter actual del patrón, si hay un borde desde el Node actual, siga el borde.
….. b) Si no hay borde, imprime «el patrón no existe en el texto» y regresa.
2) Si se han procesado todos los caracteres del patrón, es decir, hay una ruta desde la raíz para los caracteres del patrón dado, imprima todos los índices donde esté presente el patrón. Para almacenar índices, usamos una lista con cada Node que almacena índices de sufijos que comienzan en el Node.
A continuación se muestra la implementación de la idea anterior.
C++
// A simple C++ implementation of substring search using trie of suffixes
#include<iostream>
#include<list>
#define MAX_CHAR 256
using namespace std;
// A Suffix Trie (A Trie of all suffixes) Node
class SuffixTrieNode
{
private:
SuffixTrieNode *children[MAX_CHAR];
list<int> *indexes;
public:
SuffixTrieNode() // Constructor
{
// Create an empty linked list for indexes of
// suffixes starting from this node
indexes = new list<int>;
// Initialize all child pointers as NULL
for (int i = 0; i < MAX_CHAR; i++)
children[i] = NULL;
}
// A recursive function to insert a suffix of the txt
// in subtree rooted with this node
void insertSuffix(string suffix, int index);
// A function to search a pattern in subtree rooted
// with this node.The function returns pointer to a linked
// list containing all indexes where pattern is present.
// The returned indexes are indexes of last characters
// of matched text.
list<int>* search(string pat);
};
// A Trie of all suffixes
class SuffixTrie
{
private:
SuffixTrieNode root;
public:
// Constructor (Builds a trie of suffixes of the given text)
SuffixTrie(string txt)
{
// Consider all suffixes of given string and insert
// them into the Suffix Trie using recursive function
// insertSuffix() in SuffixTrieNode class
for (int i = 0; i < txt.length(); i++)
root.insertSuffix(txt.substr(i), i);
}
// Function to searches a pattern in this suffix trie.
void search(string pat);
};
// A recursive function to insert a suffix of the txt in
// subtree rooted with this node
void SuffixTrieNode::insertSuffix(string s, int index)
{
// Store index in linked list
indexes->push_back(index);
// If string has more characters
if (s.length() > 0)
{
// Find the first character
char cIndex = s.at(0);
// If there is no edge for this character, add a new edge
if (children[cIndex] == NULL)
children[cIndex] = new SuffixTrieNode();
// Recur for next suffix
children[cIndex]->insertSuffix(s.substr(1), index+1);
}
}
// A recursive function to search a pattern in subtree rooted with
// this node
list<int>* SuffixTrieNode::search(string s)
{
// If all characters of pattern have been processed,
if (s.length() == 0)
return indexes;
// if there is an edge from the current node of suffix trie,
// follow the edge.
if (children[s.at(0)] != NULL)
return (children[s.at(0)])->search(s.substr(1));
// If there is no edge, pattern doesn’t exist in text
else return NULL;
}
/* Prints all occurrences of pat in the Suffix Trie S (built for text)*/
void SuffixTrie::search(string pat)
{
// Let us call recursive search function for root of Trie.
// We get a list of all indexes (where pat is present in text) in
// variable 'result'
list<int> *result = root.search(pat);
// Check if the list of indexes is empty or not
if (result == NULL)
cout << "Pattern not found" << endl;
else
{
list<int>::iterator i;
int patLen = pat.length();
for (i = result->begin(); i != result->end(); ++i)
cout << "Pattern found at position " << *i - patLen<< endl;
}
}
// driver program to test above functions
int main()
{
// Let us build a suffix trie for text "geeksforgeeks.org"
string txt = "geeksforgeeks.org";
SuffixTrie S(txt);
cout << "Search for 'ee'" << endl;
S.search("ee");
cout << "\nSearch for 'geek'" << endl;
S.search("geek");
cout << "\nSearch for 'quiz'" << endl;
S.search("quiz");
cout << "\nSearch for 'forgeeks'" << endl;
S.search("forgeeks");
return 0;
}
Java
import java.util.LinkedList;
import java.util.List;
class SuffixTrieNode {
final static int MAX_CHAR = 256;
SuffixTrieNode[] children = new SuffixTrieNode[MAX_CHAR];
List<Integer> indexes;
SuffixTrieNode() // Constructor
{
// Create an empty linked list for indexes of
// suffixes starting from this node
indexes = new LinkedList<Integer>();
// Initialize all child pointers as NULL
for (int i = 0; i < MAX_CHAR; i++)
children[i] = null;
}
// A recursive function to insert a suffix of
// the text in subtree rooted with this node
void insertSuffix(String s, int index) {
// Store index in linked list
indexes.add(index);
// If string has more characters
if (s.length() > 0) {
// Find the first character
char cIndex = s.charAt(0);
// If there is no edge for this character,
// add a new edge
if (children[cIndex] == null)
children[cIndex] = new SuffixTrieNode();
// Recur for next suffix
children[cIndex].insertSuffix(s.substring(1),
index + 1);
}
}
// A function to search a pattern in subtree rooted
// with this node.The function returns pointer to a
// linked list containing all indexes where pattern
// is present. The returned indexes are indexes of
// last characters of matched text.
List<Integer> search(String s) {
// If all characters of pattern have been
// processed,
if (s.length() == 0)
return indexes;
// if there is an edge from the current node of
// suffix tree, follow the edge.
if (children[s.charAt(0)] != null)
return (children[s.charAt(0)]).search(s.substring(1));
// If there is no edge, pattern doesnt exist in
// text
else
return null;
}
}
// A Trie of all suffixes
class Suffix_tree{
SuffixTrieNode root = new SuffixTrieNode();
// Constructor (Builds a trie of suffixes of the
// given text)
Suffix_tree(String txt) {
// Consider all suffixes of given string and
// insert them into the Suffix Trie using
// recursive function insertSuffix() in
// SuffixTrieNode class
for (int i = 0; i < txt.length(); i++)
root.insertSuffix(txt.substring(i), i);
}
/* Prints all occurrences of pat in the Suffix Trie S
(built for text) */
void search_tree(String pat) {
// Let us call recursive search function for
// root of Trie.
// We get a list of all indexes (where pat is
// present in text) in variable 'result'
List<Integer> result = root.search(pat);
// Check if the list of indexes is empty or not
if (result == null)
System.out.println("Pattern not found");
else {
int patLen = pat.length();
for (Integer i : result)
System.out.println("Pattern found at position " +
(i - patLen));
}
}
// driver program to test above functions
public static void main(String args[]) {
// Let us build a suffix trie for text
// "geeksforgeeks.org"
String txt = "geeksforgeeks.org";
Suffix_tree S = new Suffix_tree(txt);
System.out.println("Search for 'ee'");
S.search_tree("ee");
System.out.println("\nSearch for 'geek'");
S.search_tree("geek");
System.out.println("\nSearch for 'quiz'");
S.search_tree("quiz");
System.out.println("\nSearch for 'forgeeks'");
S.search_tree("forgeeks");
}
}
// This code is contributed by Sumit Ghosh
C#
// C# implementation of the approach
using System;
using System.Collections.Generic;
class SuffixTrieNode
{
static int MAX_CHAR = 256;
public SuffixTrieNode[] children = new SuffixTrieNode[MAX_CHAR];
public List<int> indexes;
public SuffixTrieNode() // Constructor
{
// Create an empty linked list for indexes of
// suffixes starting from this node
indexes = new List<int>();
// Initialize all child pointers as NULL
for (int i = 0; i < MAX_CHAR; i++)
children[i] = null;
}
// A recursive function to insert a suffix of
// the text in subtree rooted with this node
public void insertSuffix(String s, int index)
{
// Store index in linked list
indexes.Add(index);
// If string has more characters
if (s.Length > 0)
{
// Find the first character
char cIndex = s[0];
// If there is no edge for this character,
// add a new edge
if (children[cIndex] == null)
children[cIndex] = new SuffixTrieNode();
// Recur for next suffix
children[cIndex].insertSuffix(s.Substring(1),
index + 1);
}
}
// A function to search a pattern in subtree rooted
// with this node.The function returns pointer to a
// linked list containing all indexes where pattern
// is present. The returned indexes are indexes of
// last characters of matched text.
public List<int> search(String s)
{
// If all characters of pattern have been
// processed,
if (s.Length == 0)
return indexes;
// if there is an edge from the current node of
// suffix tree, follow the edge.
if (children[s[0]] != null)
return (children[s[0]]).search(s.Substring(1));
// If there is no edge, pattern doesnt exist in
// text
else
return null;
}
}
// A Trie of all suffixes
public class Suffix_tree
{
SuffixTrieNode root = new SuffixTrieNode();
// Constructor (Builds a trie of suffixes of the
// given text)
Suffix_tree(String txt)
{
// Consider all suffixes of given string and
// insert them into the Suffix Trie using
// recursive function insertSuffix() in
// SuffixTrieNode class
for (int i = 0; i < txt.Length; i++)
root.insertSuffix(txt.Substring(i), i);
}
/* Prints all occurrences of pat in the
Suffix Trie S (built for text) */
void search_tree(String pat)
{
// Let us call recursive search function
// for root of Trie.
// We get a list of all indexes (where pat is
// present in text) in variable 'result'
List<int> result = root.search(pat);
// Check if the list of indexes is empty or not
if (result == null)
Console.WriteLine("Pattern not found");
else
{
int patLen = pat.Length;
foreach (int i in result)
Console.WriteLine("Pattern found at position " +
(i - patLen));
}
}
// Driver Code
public static void Main(String []args)
{
// Let us build a suffix trie for text
// "geeksforgeeks.org"
String txt = "geeksforgeeks.org";
Suffix_tree S = new Suffix_tree(txt);
Console.WriteLine("Search for 'ee'");
S.search_tree("ee");
Console.WriteLine("\nSearch for 'geek'");
S.search_tree("geek");
Console.WriteLine("\nSearch for 'quiz'");
S.search_tree("quiz");
Console.WriteLine("\nSearch for 'forgeeks'");
S.search_tree("forgeeks");
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
let MAX_CHAR = 256;
class SuffixTrieNode
{
// Constructor
constructor()
{
this.indexes = [];
this.children = new Array(MAX_CHAR);
for(let i = 0; i < MAX_CHAR; i++)
{
this.children[i] = 0;
}
}
// A recursive function to insert a suffix of
// the text in subtree rooted with this node
insertSuffix(s,index)
{
// Store index in linked list
this.indexes.push(index);
// If string has more characters
if (s.length > 0)
{
// Find the first character
let cIndex = s[0];
// If there is no edge for this character,
// add a new edge
if (this.children[cIndex] == null)
this.children[cIndex] = new SuffixTrieNode();
// Recur for next suffix
this.children[cIndex].insertSuffix(s.substring(1),
index + 1);
}
}
// A function to search a pattern in subtree rooted
// with this node.The function returns pointer to a
// linked list containing all indexes where pattern
// is present. The returned indexes are indexes of
// last characters of matched text.
search(s)
{
// If all characters of pattern have been
// processed,
if (s.length == 0)
return this.indexes;
// If there is an edge from the current node of
// suffix tree, follow the edge.
if (this.children[s[0]] != null)
return(this.children[s[0]].search(
s.substring(1)));
// If there is no edge, pattern doesnt exist in
// text
else
return null;
}
}
let root = new SuffixTrieNode();
// Constructor (Builds a trie of suffixes of the
// given text)
function Suffix_tree(txt)
{
// Consider all suffixes of given string and
// insert them into the Suffix Trie using
// recursive function insertSuffix() in
// SuffixTrieNode class
for(let i = 0; i < txt.length; i++)
root.insertSuffix(txt.substring(i), i);
}
/* Prints all occurrences of pat in the Suffix
Trie S (built for text) */
function search_tree(pat)
{
// Let us call recursive search function for
// root of Trie.
// We get a list of all indexes (where pat is
// present in text) in variable 'result'
let result = root.search(pat);
// Check if the list of indexes is empty or not
if (result == null)
document.write("Pattern not found<br>");
else
{
let patLen = pat.length;
for(let i of result.values())
document.write("Pattern found at position " +
(i - patLen)+"<br>");
}
}
// Driver code
// Let us build a suffix trie for text
// "geeksforgeeks.org"
let txt = "geeksforgeeks.org";
Suffix_tree(txt);
document.write("Search for 'ee'<br>");
search_tree("ee");
document.write("<br>Search for 'geek'<br>");
search_tree("geek");
document.write("<br>Search for 'quiz'<br>");
search_tree("quiz");
document.write("<br>Search for 'forgeeks'<br>");
search_tree("forgeeks");
// This code is contributed by unknown2108
</script>
Producción:
Search for 'ee' Pattern found at position 1 Pattern found at position 9 Search for 'geek' Pattern found at position 0 Pattern found at position 8 Search for 'quiz' Pattern not found Search for 'forgeeks' Pattern found at position 5
La complejidad temporal de la función de búsqueda anterior es O(m+k) donde m es la longitud del patrón y k es el número de ocurrencias del patrón en el texto.
Este artículo es una contribución de Ashish Anand. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA