Dado un gráfico acíclico conectado, un vértice de origen y un vértice de destino, su tarea es contar la cantidad de vértices entre el vértice de origen y el de destino dados mediante el método de unión disjunta.
Ejemplos:
Input : 1 4
4 5
4 2
2 6
6 3
1 3
Output : 3
In the input 6 is the total number of vertices
labeled from 1 to 6 and the next 5 lines are the connection
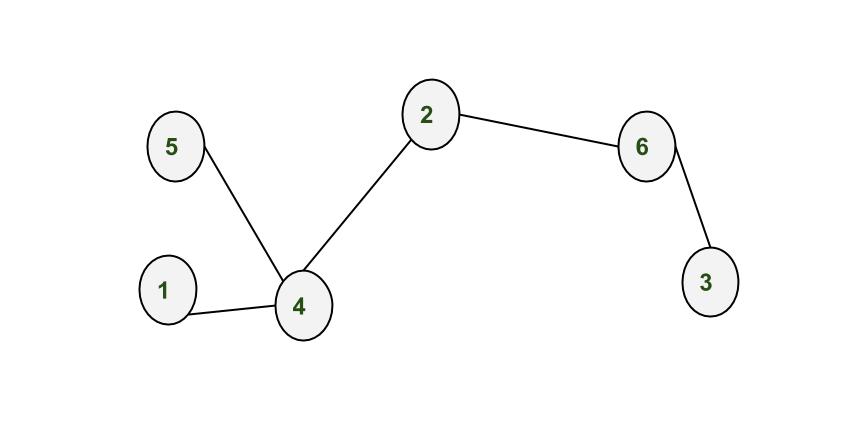
between vertices. Please see the figure for more
explanation. And in last line 1 is the source vertex
and 3 is the destination vertex. From the figure
it is clear that there are 3 nodes(4, 2, 6) present
between 1 and 3.
Para usar el método de unión disjunta, primero debemos verificar el padre de cada uno de los Nodes del gráfico dado. Podemos usar BFS para atravesar el gráfico y calcular el vértice principal de cada vértice del gráfico. Por ejemplo, si recorremos el gráfico (es decir, comenzamos nuestro BFS) desde el vértice 1, entonces 1 es el padre de 4, luego 4 es el padre de 5 y 2, nuevamente 2 es el padre de 6 y 6 es el padre de 3.
Ahora, para calcular la cantidad de Nodes entre el Node de origen y el Node de destino, debemos hacer un bucle que comience con el Node principal del Node de destino y, después de cada iteración, actualizaremos este Node con el Node principal del Node actual, manteniendo la cuenta del número. de iteraciones. La ejecución del bucle terminará cuando alcancemos el vértice de origen y la variable de recuento proporcione el número de Nodes en la ruta de conexión del Node de origen y el Node de destino.
En el método anterior, los conjuntos disjuntos son todos los conjuntos con un solo vértice, y hemos usado la operación de unión para fusionar dos conjuntos donde uno contiene el Node principal y el otro contiene el Node secundario.
A continuación se muestran las implementaciones del enfoque anterior.
C++
// C++ program to calculate number
// of nodes between two nodes
#include <bits/stdc++.h>
using namespace std;
// function to calculate no of nodes
// between two nodes
int totalNodes(vector<int> adjac[], int n,
int x, int y)
{
// x is the source node and
// y is destination node
// visited array take account of
// the nodes visited through the bfs
bool visited[n+1] = {0};
// parent array to store each nodes
// parent value
int p[n] ;
queue<int> q;
q.push(x);
// take our first node(x) as first element
// of queue and marked it as
// visited through visited[] array
visited[x] = true;
int m;
// normal bfs method starts
while (!q.empty())
{
m = q.front() ;
q.pop();
for (int i=0; i<adjac[m].size(); ++i)
{
int h = adjac[m][i];
if (!visited[h])
{
visited[h] = true;
// when new node is encountered
// we assign it's parent value
// in parent array p
p[h] = m ;
q.push(h);
}
}
}
// count variable stores the result
int count = 0;
// loop start with parent of y
// till we encountered x
int i = p[y];
while (i != x)
{
// count increases for counting
// the nodes
count++;
i = p[i];
}
return count ;
}
// Driver program to test above function
int main()
{
// adjacency list for graph
vector < int > adjac[7];
// creating graph, keeping length of
// adjacency list as (1 + no of nodes)
// as index ranges from (0 to n-1)
adjac[1].push_back(4);
adjac[4].push_back(1);
adjac[5].push_back(4);
adjac[4].push_back(5);
adjac[4].push_back(2);
adjac[2].push_back(4);
adjac[2].push_back(6);
adjac[6].push_back(2);
adjac[6].push_back(3);
adjac[3].push_back(6);
cout << totalNodes(adjac, 7, 1, 3);
return 0;
}
Java
// Java program to calculate number
// of nodes between two nodes
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Vector;
public class GFG
{
// function to calculate no of nodes
// between two nodes
static int totalNodes(Vector<Integer> adjac[],
int n, int x, int y)
{
// x is the source node and
// y is destination node
// visited array take account of
// the nodes visited through the bfs
Boolean visited[] = new Boolean[n + 1];
//filling boolean value with false
Arrays.fill(visited, false);
// parent array to store each nodes
// parent value
int p[] = new int[n];
Queue<Integer> q = new LinkedList<>();
q.add(x);
// take our first node(x) as first element
// of queue and marked it as
// visited through visited[] array
visited[x] = true;
int m;
// normal bfs method starts
while(!q.isEmpty())
{
m = q.peek();
q.poll();
for(int i=0; i < adjac[m].size() ; ++i)
{
int h = adjac[m].get(i);
if(visited[h] != true )
{
visited[h] = true;
// when new node is encountered
// we assign it's parent value
// in parent array p
p[h] = m;
q.add(h);
}
}
}
// count variable stores the result
int count = 0;
// loop start with parent of y
// till we encountered x
int i = p[y];
while(i != x)
{
// count increases for counting
// the nodes
count++;
i = p[i];
}
return count;
}
// Driver program to test above function
public static void main(String[] args)
{
// adjacency list for graph
Vector<Integer> adjac[] = new Vector[7];
//Initializing Vector for each nodes
for (int i = 0; i < 7; i++)
adjac[i] = new Vector<>();
// creating graph, keeping length of
// adjacency list as (1 + no of nodes)
// as index ranges from (0 to n-1)
adjac[1].add(4);
adjac[4].add(1);
adjac[5].add(4);
adjac[4].add(5);
adjac[4].add(2);
adjac[2].add(4);
adjac[2].add(6);
adjac[6].add(2);
adjac[6].add(3);
adjac[3].add(6);
System.out.println(totalNodes(adjac, 7, 1, 3));
}
}
// This code is contributed by Sumit Ghosh
Python3
# Python3 program to calculate number # of nodes between two nodes import queue # function to calculate no of nodes # between two nodes def totalNodes(adjac, n, x, y): # x is the source node and # y is destination node # visited array take account of # the nodes visited through the bfs visited = [0] * (n + 1) # parent array to store each nodes # parent value p = [None] * n q = queue.Queue() q.put(x) # take our first node(x) as first # element of queue and marked it as # visited through visited[] array visited[x] = True m = None # normal bfs method starts while (not q.empty()): m = q.get() for i in range(len(adjac[m])): h = adjac[m][i] if (not visited[h]): visited[h] = True # when new node is encountered # we assign it's parent value # in parent array p p[h] = m q.put(h) # count variable stores the result count = 0 # loop start with parent of y # till we encountered x i = p[y] while (i != x): # count increases for counting # the nodes count += 1 i = p[i] return count # Driver Code if __name__ == '__main__': # adjacency list for graph adjac = [[] for i in range(7)] # creating graph, keeping length of # adjacency list as (1 + no of nodes) # as index ranges from (0 to n-1) adjac[1].append(4) adjac[4].append(1) adjac[5].append(4) adjac[4].append(5) adjac[4].append(2) adjac[2].append(4) adjac[2].append(6) adjac[6].append(2) adjac[6].append(3) adjac[3].append(6) print(totalNodes(adjac, 7, 1, 3)) # This code is contributed by PranchalK
C#
// C# program to calculate number
// of nodes between two nodes
using System;
using System.Collections.Generic;
class GFG
{
// function to calculate no of nodes
// between two nodes
static int totalNodes(List<int> []adjac,
int n, int x, int y)
{
// x is the source node and
// y is destination node
// visited array take account of
// the nodes visited through the bfs
Boolean []visited = new Boolean[n + 1];
// parent array to store each nodes
// parent value
int []p = new int[n];
Queue<int> q = new Queue<int>();
q.Enqueue(x);
// take our first node(x) as first element
// of queue and marked it as
// visited through visited[] array
visited[x] = true;
int m, i;
// normal bfs method starts
while(q.Count != 0)
{
m = q.Peek();
q.Dequeue();
for(i = 0; i < adjac[m].Count ; ++i)
{
int h = adjac[m][i];
if(visited[h] != true )
{
visited[h] = true;
// when new node is encountered
// we assign it's parent value
// in parent array p
p[h] = m;
q.Enqueue(h);
}
}
}
// count variable stores the result
int count = 0;
// loop start with parent of y
// till we encountered x
i = p[y];
while(i != x)
{
// count increases for counting
// the nodes
count++;
i = p[i];
}
return count;
}
// Driver Code
public static void Main(String[] args)
{
// adjacency list for graph
List<int> []adjac = new List<int>[7];
//Initializing Vector for each nodes
for (int i = 0; i < 7; i++)
adjac[i] = new List<int>();
// creating graph, keeping length of
// adjacency list as (1 + no of nodes)
// as index ranges from (0 to n-1)
adjac[1].Add(4);
adjac[4].Add(1);
adjac[5].Add(4);
adjac[4].Add(5);
adjac[4].Add(2);
adjac[2].Add(4);
adjac[2].Add(6);
adjac[6].Add(2);
adjac[6].Add(3);
adjac[3].Add(6);
Console.WriteLine(totalNodes(adjac, 7, 1, 3));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program to calculate number
// of nodes between two nodes
// function to calculate no of nodes
// between two nodes
function totalNodes(adjac,n,x,y)
{
// x is the source node and
// y is destination node
// visited array take account of
// the nodes visited through the bfs
let visited = new Array(n + 1);
// filling boolean value with false
for(let i=0;i<n+1;i++)
{
visited[i]=false;
}
// parent array to store each nodes
// parent value
let p = new Array(n);
let q = [];
q.push(x);
// take our first node(x) as first element
// of queue and marked it as
// visited through visited[] array
visited[x] = true;
let m;
// normal bfs method starts
while(q.length!=0)
{
m = q[0];
q.shift();
for(let i=0; i < adjac[m].length ; ++i)
{
let h = adjac[m][i];
if(visited[h] != true )
{
visited[h] = true;
// when new node is encountered
// we assign it's parent value
// in parent array p
p[h] = m;
q.push(h);
}
}
}
// count variable stores the result
let count = 0;
// loop start with parent of y
// till we encountered x
let i = p[y];
while(i != x)
{
// count increases for counting
// the nodes
count++;
i = p[i];
}
return count;
}
// Driver program to test above function
let adjac = new Array(7);
//Initializing Vector for each nodes
for (let i = 0; i < 7; i++)
adjac[i] = [];
// creating graph, keeping length of
// adjacency list as (1 + no of nodes)
// as index ranges from (0 to n-1)
adjac[1].push(4);
adjac[4].push(1);
adjac[5].push(4);
adjac[4].push(5);
adjac[4].push(2);
adjac[2].push(4);
adjac[2].push(6);
adjac[6].push(2);
adjac[6].push(3);
adjac[3].push(6);
document.write(totalNodes(adjac, 7, 1, 3));
// This code is contributed by rag2127
</script>
3
Complejidad de tiempo: O(n), donde n es el número total de Nodes en el gráfico.
Este artículo es una contribución de Surya Priy . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA