Dado un gráfico acíclico conectado que consta de vértices V y aristas E , un vértice de origen src y un vértice de destino dest , la tarea es contar el número de vértices entre el origen y el vértice de destino dados en el gráfico.
Ejemplos :
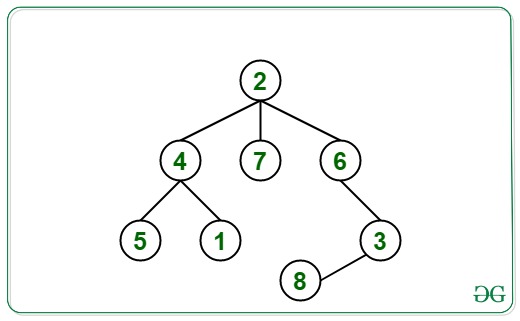
Entrada: V = 8, E = 7, origen = 7, destino = 8, bordes[][] ={{1 4}, {4, 5}, {4, 2}, {2, 6}, {6 , 3}, {2, 7}, {3, 8}}
Salida: 3
Explicación:
La ruta entre 7 y 8 es 7 -> 2 -> 6 -> 3 -> 8.
Entonces, el número de Nodes entre 7 y 8 es 3Entrada: V = 8, E = 7, origen = 5, destino = 2, bordes[][] ={{1 4}, {4, 5}, {4, 2}, {2, 6}, {6 , 3}, {2, 7}, {3, 8}}
Salida: 1
Explicación:
La ruta entre 5 y 2 es 5 -> 4 -> 2.
Entonces, el número de Nodes entre 5 y 2 es 1.
Enfoque: el problema también se puede resolver utilizando el método de unión disjunta como se indica en este artículo. Otro enfoque para este problema es resolverlo utilizando el método de búsqueda en profundidad primero . Siga los pasos a continuación para resolver este problema:
- Inicialice una array visitada vis[] para marcar qué Nodes ya han sido visitados. Marque todos los Nodes como 0, es decir, no visitados.
- Realice un DFS para encontrar la cantidad de Nodes presentes en la ruta entre src y dest.
- El número de Nodes entre src y dest es igual a la diferencia entre la longitud de la ruta entre ellos y 2, es decir, (pathSrcToDest – 2 ).
- Dado que el gráfico es acíclico y está conectado, siempre habrá un solo camino entre src y dest.
A continuación se muestra la implementación del algoritmo anterior.
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to return the count of nodes
// in the path from source to destination
int dfs(int src, int dest, int* vis,
vector<int>* adj)
{
// Mark the node visited
vis[src] = 1;
// If dest is reached
if (src == dest) {
return 1;
}
// Traverse all adjacent nodes
for (int u : adj[src]) {
// If not already visited
if (!vis[u]) {
int temp = dfs(u, dest, vis, adj);
// If there is path, then
// include the current node
if (temp != 0) {
return temp + 1;
}
}
}
// Return 0 if there is no path
// between src and dest through
// the current node
return 0;
}
// Function to return the
// count of nodes between two
// given vertices of the acyclic Graph
int countNodes(int V, int E, int src, int dest,
int edges[][2])
{
// Initialize an adjacency list
vector<int> adj[V + 1];
// Populate the edges in the list
for (int i = 0; i < E; i++) {
adj[edges[i][0]].push_back(edges[i][1]);
adj[edges[i][1]].push_back(edges[i][0]);
}
// Mark all the nodes as not visited
int vis[V + 1] = { 0 };
// Count nodes in the path from src to dest
int count = dfs(src, dest, vis, adj);
// Return the nodes between src and dest
return count - 2;
}
// Driver Code
int main()
{
// Given number of vertices and edges
int V = 8, E = 7;
// Given source and destination vertices
int src = 5, dest = 2;
// Given edges
int edges[][2]
= { { 1, 4 }, { 4, 5 },
{ 4, 2 }, { 2, 6 },
{ 6, 3 }, { 2, 7 },
{ 3, 8 } };
cout << countNodes(V, E, src, dest, edges);
return 0;
}
Java
// Java program for the above approach
import java.util.Vector;
class GFG{
// Function to return the count of nodes
// in the path from source to destination
static int dfs(int src, int dest, int []vis,
Vector<Integer> []adj)
{
// Mark the node visited
vis[src] = 1;
// If dest is reached
if (src == dest)
{
return 1;
}
// Traverse all adjacent nodes
for (int u : adj[src])
{
// If not already visited
if (vis[u] == 0)
{
int temp = dfs(u, dest,
vis, adj);
// If there is path, then
// include the current node
if (temp != 0)
{
return temp + 1;
}
}
}
// Return 0 if there is no path
// between src and dest through
// the current node
return 0;
}
// Function to return the
// count of nodes between two
// given vertices of the acyclic Graph
static int countNodes(int V, int E,
int src, int dest,
int edges[][])
{
// Initialize an adjacency list
Vector<Integer> []adj = new Vector[V + 1];
for (int i = 0; i < adj.length; i++)
adj[i] = new Vector<Integer>();
// Populate the edges in the list
for (int i = 0; i < E; i++)
{
adj[edges[i][0]].add(edges[i][1]);
adj[edges[i][1]].add(edges[i][0]);
}
// Mark all the nodes as
// not visited
int vis[] = new int[V + 1];
// Count nodes in the path
// from src to dest
int count = dfs(src, dest,
vis, adj);
// Return the nodes
// between src and dest
return count - 2;
}
// Driver Code
public static void main(String[] args)
{
// Given number of vertices and edges
int V = 8, E = 7;
// Given source and destination vertices
int src = 5, dest = 2;
// Given edges
int edges[][] = {{1, 4}, {4, 5},
{4, 2}, {2, 6},
{6, 3}, {2, 7},
{3, 8}};
System.out.print(countNodes(V, E,
src, dest,
edges));
}
}
// This code is contributed by shikhasingrajput
Python3
# Python3 program for the above approach # Function to return the count of nodes # in the path from source to destination def dfs(src, dest, vis, adj): # Mark the node visited vis[src] = 1 # If dest is reached if (src == dest): return 1 # Traverse all adjacent nodes for u in adj[src]: # If not already visited if not vis[u]: temp = dfs(u, dest, vis, adj) # If there is path, then # include the current node if (temp != 0): return temp + 1 # Return 0 if there is no path # between src and dest through # the current node return 0 # Function to return the # count of nodes between two # given vertices of the acyclic Graph def countNodes(V, E, src, dest, edges): # Initialize an adjacency list adj = [[] for i in range(V + 1)] # Populate the edges in the list for i in range(E): adj[edges[i][0]].append(edges[i][1]) adj[edges[i][1]].append(edges[i][0]) # Mark all the nodes as not visited vis = [0] * (V + 1) # Count nodes in the path from src to dest count = dfs(src, dest, vis, adj) # Return the nodes between src and dest return count - 2 # Driver Code if __name__ == '__main__': # Given number of vertices and edges V = 8 E = 7 # Given source and destination vertices src = 5 dest = 2 # Given edges edges = [ [ 1, 4 ], [ 4, 5 ], [ 4, 2 ], [ 2, 6 ], [ 6, 3 ], [ 2, 7 ], [ 3, 8 ] ] print(countNodes(V, E, src, dest, edges)) # This code is contributed by mohit kumar 29
C#
// C# program for
// the above approach
using System;
using System.Collections.Generic;
class GFG{
// Function to return the count of nodes
// in the path from source to destination
static int dfs(int src, int dest,
int []vis, List<int> []adj)
{
// Mark the node visited
vis[src] = 1;
// If dest is reached
if (src == dest)
{
return 1;
}
// Traverse all adjacent nodes
foreach (int u in adj[src])
{
// If not already visited
if (vis[u] == 0)
{
int temp = dfs(u, dest,
vis, adj);
// If there is path, then
// include the current node
if (temp != 0)
{
return temp + 1;
}
}
}
// Return 0 if there is no path
// between src and dest through
// the current node
return 0;
}
// Function to return the
// count of nodes between two
// given vertices of the acyclic Graph
static int countNodes(int V, int E,
int src, int dest,
int [,]edges)
{
// Initialize an adjacency list
List<int> []adj = new List<int>[V + 1];
for (int i = 0; i < adj.Length; i++)
adj[i] = new List<int>();
// Populate the edges in the list
for (int i = 0; i < E; i++)
{
adj[edges[i, 0]].Add(edges[i, 1]);
adj[edges[i, 1]].Add(edges[i, 0]);
}
// Mark all the nodes as
// not visited
int []vis = new int[V + 1];
// Count nodes in the path
// from src to dest
int count = dfs(src, dest,
vis, adj);
// Return the nodes
// between src and dest
return count - 2;
}
// Driver Code
public static void Main(String[] args)
{
// Given number of vertices and edges
int V = 8, E = 7;
// Given source and destination vertices
int src = 5, dest = 2;
// Given edges
int [,]edges = {{1, 4}, {4, 5},
{4, 2}, {2, 6},
{6, 3}, {2, 7},
{3, 8}};
Console.Write(countNodes(V, E, src,
dest, edges));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program for the above approach
// Function to return the count of nodes
// in the path from source to destination
function dfs(src,dest,vis,adj)
{
// Mark the node visited
vis[src] = 1;
// If dest is reached
if (src == dest)
{
return 1;
}
// Traverse all adjacent nodes
for (let u=0;u< adj[src].length;u++)
{
// If not already visited
if (vis[adj[src][u]] == 0)
{
let temp = dfs(adj[src][u], dest,
vis, adj);
// If there is path, then
// include the current node
if (temp != 0)
{
return temp + 1;
}
}
}
// Return 0 if there is no path
// between src and dest through
// the current node
return 0;
}
// Function to return the
// count of nodes between two
// given vertices of the acyclic Graph
function countNodes(V,E,src,dest,edges)
{
// Initialize an adjacency list
let adj = new Array(V + 1);
for (let i = 0; i < adj.length; i++)
adj[i] = [];
// Populate the edges in the list
for (let i = 0; i < E; i++)
{
adj[edges[i][0]].push(edges[i][1]);
adj[edges[i][1]].push(edges[i][0]);
}
// Mark all the nodes as
// not visited
let vis = new Array(V + 1);
for(let i=0;i<vis.length;i++)
{
vis[i]=0;
}
// Count nodes in the path
// from src to dest
let count = dfs(src, dest,
vis, adj);
// Return the nodes
// between src and dest
return count - 2;
}
// Driver Code
// Given number of vertices and edges
let V = 8, E = 7;
// Given source and destination vertices
let src = 5, dest = 2;
// Given edges
let edges = [[1, 4], [4, 5],
[4, 2], [2, 6],
[6, 3], [2, 7],
[3, 8]];
document.write(countNodes(V, E,
src, dest,
edges));
// This code is contributed by unknown2108
</script>
1
Complejidad temporal: O(V+E)
Espacio auxiliar: O(V)