Calcule el promedio, la varianza y la desviación estándar en la programación R

El lenguaje de programación R es un lenguaje de programación de código abierto que se usa ampliamente como software estadístico y herramienta de análisis de datos. R generalmente viene con la interfaz de línea de comandos. R está disponible en plataformas ampliamente utilizadas como Windows, Linux y macOS. El lenguaje R proporciona métodos muy sencillos para calcular el promedio, la varianza y la desviación estándar.

Promedio en Programación R

Promediar un número que expresa el valor central o típico de un conjunto de datos, en particular la moda, la mediana o (más comúnmente) la media, que se calcula dividiendo la suma de los valores del conjunto por su número. La fórmula básica para el promedio de n números x1, x2, ……xn es

Ejemplo:

Supongamos que hay 8 puntos de datos,

2, 4, 4, 4, 5, 5, 7, 9

El promedio de estos 8 puntos de datos es,

Promedio de cálculo en programación R

Para calcular el promedio de valores, R proporciona una función predefinida mean() . Esta función toma un vector numérico como argumento y da como resultado el promedio/media de ese vector.

Sintaxis: mean(x, na.rm)

Parámetros:

• x: vector numérico
• na.rm: valor booleano para ignorar el valor NA

Ejemplo 1:

# R program to get average of a list
 
# Taking a list of elements
list = c(2, 4, 4, 4, 5, 5, 7, 9)
 
# Calculating average using mean()
print(mean(list))

 Producción:

[1] 5

Ejemplo 2:

# R program to get average of a list
 
# Taking a list of elements
list = c(2, 40, 2, 502, 177, 7, 9)
 
# Calculating average using mean()
print(mean(list))

 Producción:

[1] 105.5714

Variación en el lenguaje de programación R

La varianza es la suma de los cuadrados de las diferencias entre todos los números y medias. La fórmula matemática para la varianza es la siguiente,

dónde,

N es el número total de elementos o frecuencia de distribución. 

Ejemplo:

Consideremos el mismo conjunto de datos que hemos tomado en promedio. Primero, calcule las desviaciones de cada punto de datos de la media y eleve al cuadrado el resultado de cada uno,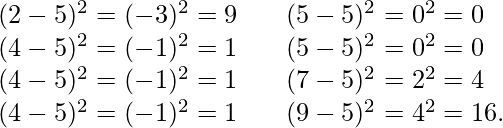
[Tex]varianza = \frac{9 + 1 + 1 + 1 + 0 + 0 + 4 + 16}{8} = 4[ /Texas]

Cálculo de la varianza en la programación R

Uno puede calcular la varianza usando la función var() en R.

Sintaxis: var(x)

Parámetros:

x: vector numérico

Ejemplo 1:

# R program to get variance of a list
 
# Taking a list of elements
list = c(2, 4, 4, 4, 5, 5, 7, 9)
 
# Calculating variance using var()
print(var(list))

 Producción:

[1] 4.571429

Ejemplo 2:

# R program to get variance of a list
 
# Taking a list of elements
list = c(212, 231, 234, 564, 235)
 
# Calculating variance using var()
print(var(list))

 Producción:

[1] 22666.7

Desviación estándar en lenguaje de programación R

La desviación estándar es la raíz cuadrada de la varianza. Es una medida de la medida en que los datos varían de la media. La fórmula matemática para calcular la desviación estándar es la siguiente,  

Ejemplo:

Desviación estándar para los datos anteriores,

Cálculo de la desviación estándar en R

Uno puede calcular la desviación estándar usando la función sd() en R.

Sintaxis: sd(x)

Parámetros:

x: vector numérico

Ejemplo 1:

# R program to get
# standard deviation of a list
 
# Taking a list of elements
list = c(2, 4, 4, 4, 5, 5, 7, 9)
 
# Calculating standard
# deviation using sd()
print(sd(list))

 Producción:

[1] 2.13809

Ejemplo 2:

# R program to get
# standard deviation of a list
 
# Taking a list of elements
list = c(290, 124, 127, 899)
 
# Calculating standard
# deviation using sd()
print(sd(list))

 Producción:

[1] 367.6076