Dada una array de n enteros positivos y un número k . Encuentre el número mínimo de intercambios requeridos para juntar todos los números menores o iguales a k .
Input: arr[] = {2, 1, 5, 6, 3}, k = 3
Output: 1
Explanation:
To bring elements 2, 1, 3 together, swap
element '5' with '3' such that final array
will be-
arr[] = {2, 1, 3, 6, 5}
Input: arr[] = {2, 7, 9, 5, 8, 7, 4}, k = 5
Output: 2
Una solución simple es contar primero todos los elementos menores o iguales que k (digamos ‘bueno’). Ahora recorra cada subarreglo e intercambie aquellos elementos cuyo valor sea mayor que k . La complejidad temporal de este enfoque es O(n 2 ) Un enfoque
eficiente es utilizar la técnica de dos punteros y una ventana deslizante . La complejidad temporal de este enfoque es O(n)
- Encuentre el conteo de todos los elementos que son menores o iguales a ‘k’. Digamos que el conteo es ‘cnt’
- Usando la técnica de dos punteros para una ventana de longitud ‘cnt’, cada vez lleve un registro de cuántos elementos en este rango son mayores que ‘k’. Digamos que el conteo total es ‘malo’.
- Repita el paso 2, para cada ventana de longitud ‘cnt’ y tome un mínimo de cuenta ‘malo’ entre ellos. Esta será la respuesta final.
diagrama de flujo
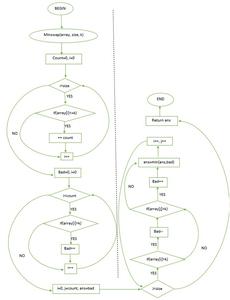
Intercambio mínimo de diagrama de flujo
C++
// C++ program to find minimum swaps required
// to club all elements less than or equals
// to k together
#include <iostream>
using namespace std;
// Utility function to find minimum swaps
// required to club all elements less than
// or equals to k together
int minSwap(int *arr, int n, int k) {
// Find count of elements which are
// less than equals to k
int count = 0;
for (int i = 0; i < n; ++i)
if (arr[i] <= k)
++count;
// Find unwanted elements in current
// window of size 'count'
int bad = 0;
for (int i = 0; i < count; ++i)
if (arr[i] > k)
++bad;
// Initialize answer with 'bad' value of
// current window
int ans = bad;
for (int i = 0, j = count; j < n; ++i, ++j) {
// Decrement count of previous window
if (arr[i] > k)
--bad;
// Increment count of current window
if (arr[j] > k)
++bad;
// Update ans if count of 'bad'
// is less in current window
ans = min(ans, bad);
}
return ans;
}
// Driver code
int main() {
int arr[] = {2, 1, 5, 6, 3};
int n = sizeof(arr) / sizeof(arr[0]);
int k = 3;
cout << minSwap(arr, n, k) << "\n";
int arr1[] = {2, 7, 9, 5, 8, 7, 4};
n = sizeof(arr1) / sizeof(arr1[0]);
k = 5;
cout << minSwap(arr1, n, k);
return 0;
}
Java
// Java program to find minimum
// swaps required to club all
// elements less than or equals
// to k together
import java.lang.*;
class GFG {
// Utility function to find minimum swaps
// required to club all elements less than
// or equals to k together
static int minSwap(int arr[], int n, int k) {
// Find count of elements which are
// less than equals to k
int count = 0;
for (int i = 0; i < n; ++i)
if (arr[i] <= k)
++count;
// Find unwanted elements in current
// window of size 'count'
int bad = 0;
for (int i = 0; i < count; ++i)
if (arr[i] > k)
++bad;
// Initialize answer with 'bad' value of
// current window
int ans = bad;
for (int i = 0, j = count; j < n; ++i, ++j) {
// Decrement count of previous window
if (arr[i] > k)
--bad;
// Increment count of current window
if (arr[j] > k)
++bad;
// Update ans if count of 'bad'
// is less in current window
ans = Math.min(ans, bad);
}
return ans;
}
// Driver code
public static void main(String[] args)
{
int arr[] = {2, 1, 5, 6, 3};
int n = arr.length;
int k = 3;
System.out.print(minSwap(arr, n, k) + "\n");
int arr1[] = {2, 7, 9, 5, 8, 7, 4};
n = arr1.length;
k = 5;
System.out.print(minSwap(arr1, n, k));
}
}
// This code is contributed by Anant Agarwal.
Python3
# Python3 program to find # minimum swaps required # to club all elements less # than or equals to k together # Utility function to find # minimum swaps required to # club all elements less than # or equals to k together def minSwap(arr, n, k) : # Find count of elements # which are less than # equals to k count = 0 for i in range(0, n) : if (arr[i] <= k) : count = count + 1 # Find unwanted elements # in current window of # size 'count' bad = 0 for i in range(0, count) : if (arr[i] > k) : bad = bad + 1 # Initialize answer with # 'bad' value of current # window ans = bad j = count for i in range(0, n) : if(j == n) : break # Decrement count of # previous window if (arr[i] > k) : bad = bad - 1 # Increment count of # current window if (arr[j] > k) : bad = bad + 1 # Update ans if count # of 'bad' is less in # current window ans = min(ans, bad) j = j + 1 return ans # Driver code arr = [2, 1, 5, 6, 3] n = len(arr) k = 3 print (minSwap(arr, n, k)) arr1 = [2, 7, 9, 5, 8, 7, 4] n = len(arr1) k = 5 print (minSwap(arr1, n, k)) # This code is contributed by # Manish Shaw(manishshaw1)
C#
// C# program to find minimum
// swaps required to club all
// elements less than or equals
// to k together
using System;
class GFG {
// Utility function to find minimum swaps
// required to club all elements less than
// or equals to k together
static int minSwap(int []arr, int n, int k) {
// Find count of elements which are
// less than equals to k
int count = 0;
for (int i = 0; i < n; ++i)
if (arr[i] <= k)
++count;
// Find unwanted elements in current
// window of size 'count'
int bad = 0;
for (int i = 0; i < count; ++i)
if (arr[i] > k)
++bad;
// Initialize answer with 'bad' value of
// current window
int ans = bad;
for (int i = 0, j = count; j < n; ++i, ++j) {
// Decrement count of previous window
if (arr[i] > k)
--bad;
// Increment count of current window
if (arr[j] > k)
++bad;
// Update ans if count of 'bad'
// is less in current window
ans = Math.Min(ans, bad);
}
return ans;
}
// Driver code
public static void Main()
{
int []arr = {2, 1, 5, 6, 3};
int n = arr.Length;
int k = 3;
Console.WriteLine(minSwap(arr, n, k));
int []arr1 = {2, 7, 9, 5, 8, 7, 4};
n = arr1.Length;
k = 5;
Console.WriteLine(minSwap(arr1, n, k));
}
}
// This code is contributed by vt_m.
PHP
<?php
// PHP program to find
// minimum swaps required
// to club all elements
// less than or equals
// to k together
// Utility function to
// find minimum swaps
// required to club all
// elements less than
// or equals to k together
function minSwap($arr, $n, $k)
{
// Find count of elements
// which are less than
// equals to k
$count = 0;
for ($i = 0; $i < $n; ++$i)
if ($arr[$i] <= $k)
++$count;
// Find unwanted elements in current
// window of size 'count'
$bad = 0;
for ($i = 0; $i < $count; ++$i)
if ($arr[$i] > $k)
++$bad;
// Initialize answer
// with 'bad' value of
// current window
$ans = $bad;
for ($i = 0, $j = $count; $j < $n;
++$i, ++$j)
{
// Decrement count of
// previous window
if ($arr[$i] > $k)
--$bad;
// Increment count of
// current window
if ($arr[$j] > $k)
++$bad;
// Update ans if count of 'bad'
// is less in current window
$ans = min($ans, $bad);
}
return $ans;
}
// Driver code
$arr = array(2, 1, 5, 6, 3);
$n = sizeof($arr);
$k = 3;
echo(minSwap($arr, $n, $k) . "\n");
$arr1 = array(2, 7, 9, 5, 8, 7, 4);
$n = sizeof($arr1);
$k = 5;
echo(minSwap($arr1, $n, $k));
// This code is contributed by Ajit.
?>
Javascript
<script>
// Utility function to find minimum swaps
// required to club all elements less than
// or equals to k together
function minSwap(arr, n, k) {
// Find count of elements which are
// less than equals to k
var count = 0;
for (var i = 0; i < n; ++i)
if (arr[i] <= k)
++count;
// Find unwanted elements in current
// window of size 'count'
var bad = 0;
for (var i = 0; i < count; ++i)
if (arr[i] > k)
++bad;
// Initialize answer with 'bad' value of
// current window
var ans = bad;
for (var i = 0, j = count; j < n; ++i, ++j) {
// Decrement count of previous window
if (arr[i] > k)
--bad;
// Increment count of current window
if (arr[j] > k)
++bad;
// Update ans if count of 'bad'
// is less in current window
ans = Math.min(ans, bad);
}
return ans;
}
// Driver code
var arr=[2, 1, 5, 6, 3];
var n =5;
var k = 3;
document.write(minSwap(arr, n, k) + "<br>");
var arr1 = [2, 7, 9, 5, 8, 7, 4];
n = 7;
k = 5;
document.write(minSwap(arr1, n, k));
// This code is by Akshit Nikita Saxena
</script>
1 2
Otro enfoque para resolver este problema es simplemente usar la técnica de ventana deslizante simple y sin usar ningún puntero que se pueda hacer en tiempo O (N).
- Nombraremos nuestra ventana deslizante como tamaño de bola de nieve. Nuestro tamaño de bola de nieve comenzará desde 0 y aumentaremos su tamaño a medida que encontremos cualquier elemento mayor que K. Nuestra ventana de bola de nieve tendrá solo elementos que sean mayores que K.
- Si vemos un elemento arr[i] con un valor menor que k , intercambiaremos el elemento arr[i] con nuestro primer elemento de bola de nieve que tiene un valor mayor que K.
- mantendremos la variable de conteo para realizar un seguimiento del número de intercambios.
C++
#include <iostream>
using namespace std;
int minSwap(int arr[], int n, int k)
{
int snowBallSize = 0; // initially snowBallsize is 0
int count = 0;
for (int i = 0; i < n; i++)
{
// we will increment our
// snowBall only if we see an
// element greater than K
if (arr[i] > k) {
snowBallSize++;
}
// this case will handle if we see an element less than <= k,
// then we will swap the element arr[i] which is less
// than K, with our first element of snowBall window which is greater than K.
else if (snowBallSize > 0) {
int tmp = arr[i];
arr[i] = arr[i - snowBallSize];
arr[i - snowBallSize] = tmp;
count++;
}
}
return count;
}
int main()
{
int arr1[] = { 2, 7, 9, 5, 8, 7, 4 };
int n = sizeof(arr1)/sizeof(arr1[0]);
int k = 5;
cout << "min swaps = " << minSwap(arr1, n, k) << "\n";
cout << "Array after min swaps = ";
for(int i=0;i<n;i++) cout << arr1[i] << " ";
cout << "\n";
int arr2[] = {2, 1, 5, 6, 3};
n = sizeof(arr2)/sizeof(arr2[0]);
k = 3;
cout << "min swaps = " << minSwap(arr2, n, k) << "\n";
cout << "Array after min swaps = ";
for(int i=0;i<n;i++) cout << arr2[i] << " ";
return 0;
}
// This code is contributed by aditya942003patil
Java
/*package whatever //do not write package name here */
import java.io.*;
import java.util.*;
class GFG {
private static int minSwap(int[] arr, int n, int k)
{
int snowBallSize = 0; // initially snowBallsize is 0
int count = 0;
for (int i = 0; i < n; i++) {
// we will increment our
// snowBall only if we see an
// element greater than K
if (arr[i] > k) {
snowBallSize++;
}
// this case will handle if we see an element less than <= k,
// then we will swap the element arr[i] which is less
// than K, with our first element of snowBall window which is greater than K.
else if (snowBallSize > 0) {
int tmp = arr[i];
arr[i] = arr[i - snowBallSize];
arr[i - snowBallSize] = tmp;
count++;
}
}
return count;
}
public static void main(String[] args)
{
int arr1[] = { 2, 7, 9, 5, 8, 7, 4 };
int n = arr1.length;
int k = 5;
System.out.println("min swaps = "
+ minSwap(arr1, n, k));
System.out.println("Array after min swaps = "
+ Arrays.toString(arr1));
int arr2[] = {2, 1, 5, 6, 3};
n = arr2.length;
k = 3;
System.out.println("min swaps = "
+ minSwap(arr2, n, k));
System.out.println("Array after min swaps = "
+ Arrays.toString(arr2));
}
}
min swaps = 2 Array after min swaps = [2, 5, 4, 7, 8, 7, 9] min swaps = 1 Array after min swaps = [2, 1, 3, 6, 5]
Publicación traducida automáticamente
Artículo escrito por Shubham Bansal 13 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA