Hay una array rectangular am*n cuya ubicación superior izquierda (inicio) es (1, 1) y la ubicación inferior derecha (final) es (m*n). Hay k círculos cada uno con radio r. Encuentra si hay algún camino de principio a fin sin tocar ningún círculo.
La entrada contiene valores de m, n, k, r y dos arrays de números enteros X e Y, cada uno de longitud k. (X[i], Y[i]) es el centro del i -ésimo círculo.
Fuente : Entrevista Directi
Ejemplos:
Input : m = 5, n = 5, k = 2, r = 1,
X = {1, 3}, Y = {3, 3}
Output : Possible
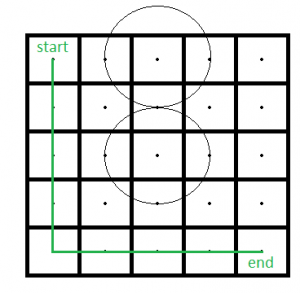
Aquí hay un camino desde el punto de inicio hasta el final.
Input : m = 5, n = 5, k = 2, r = 1,
X = {1, 1}, Y = {2, 3}.
Output : Not Possible

Enfoque: Verifique si el centro de una celda (i, j) del rectángulo se encuentra dentro de alguno de los círculos, luego no atraviese esa celda y márquela como ‘bloqueada’. Marque el resto de las celdas inicialmente como ‘no visitadas’. Luego use BFS para encontrar la ruta más corta de cada celda desde la posición inicial. Si se visita la celda final, devolveremos «Posible», de lo contrario, «No posible».
Algoritmo:
- Tome una array de tamaño m*n. Inicializar todas las celdas a 0.
- Para cada celda del rectángulo, compruebe si se encuentra dentro de algún círculo o no (calculando la distancia de esa celda a cada círculo). Si se encuentra dentro de cualquier círculo, cambie el valor de esa celda a -1 («bloqueado»).
- Ahora, aplique BFS desde la celda inicial y, si se puede llegar a una celda, cambie el valor de esa celda a 1.
- Si el valor de la celda final es 1, devuelva ‘Posible’; de lo contrario, devuelva ‘No posible’.
A continuación se muestra la implementación de la idea anterior:
C++
// C++ program to find out path in
// a rectangle containing circles.
#include <iostream>
#include <math.h>
#include <vector>
using namespace std;
// Function to find out if there is
// any possible path or not.
bool isPossible(int m, int n, int k, int r, vector<int> X,
vector<int> Y)
{
// Take an array of m*n size and
// initialize each element to 0.
int rect[m][n] = { 0 };
// Now using Pythagorean theorem find if a
// cell touches or within any circle or not.
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
for (int p = 0; p < k; p++) {
if (sqrt((pow((X[p] - 1 - i), 2)
+ pow((Y[p] - 1 - j), 2)))
<= r) {
rect[i][j] = -1;
}
}
}
}
// If the starting cell comes within
// any circle return false.
if (rect[0][0] == -1)
return false;
// Now use BFS to find if there
// is any possible path or not.
// Initialize the queue which holds
// the discovered cells whose neighbors
// are not discovered yet.
vector<vector<int> > qu;
rect[0][0] = 1;
qu.push_back({ 0, 0 });
// Discover cells until queue is not empty
while (!qu.empty()) {
vector<int> arr = qu.front();
qu.erase(qu.begin());
int elex = arr[0];
int eley = arr[1];
// Discover the eight adjacent nodes.
// check top-left cell
if ((elex > 0) && (eley > 0)
&& (rect[elex - 1][eley - 1] == 0)) {
rect[elex - 1][eley - 1] = 1;
vector<int> v = { elex - 1, eley - 1 };
qu.push_back(v);
}
// check top cell
if ((elex > 0) && (rect[elex - 1][eley] == 0)) {
rect[elex - 1][eley] = 1;
vector<int> v = { elex - 1, eley };
qu.push_back(v);
}
// check top-right cell
if ((elex > 0) && (eley < n - 1)
&& (rect[elex - 1][eley + 1] == 0)) {
rect[elex - 1][eley + 1] = 1;
vector<int> v = { elex - 1, eley + 1 };
qu.push_back(v);
}
// check left cell
if ((eley > 0) && (rect[elex][eley - 1] == 0)) {
rect[elex][eley - 1] = 1;
vector<int> v = { elex, eley - 1 };
qu.push_back(v);
}
// check right cell
if ((eley < n - 1) && (rect[elex][eley + 1] == 0)) {
rect[elex][eley + 1] = 1;
vector<int> v = { elex, eley + 1 };
qu.push_back(v);
}
// check bottom-left cell
if ((elex < m - 1) && (eley > 0)
&& (rect[elex + 1][eley - 1] == 0)) {
rect[elex + 1][eley - 1] = 1;
vector<int> v = { elex + 1, eley - 1 };
qu.push_back(v);
}
// check bottom cell
if ((elex < m - 1) && (rect[elex + 1][eley] == 0)) {
rect[elex + 1][eley] = 1;
vector<int> v = { elex + 1, eley };
qu.push_back(v);
}
// check bottom-right cell
if ((elex < m - 1) && (eley < n - 1)
&& (rect[elex + 1][eley + 1] == 0)) {
rect[elex + 1][eley + 1] = 1;
vector<int> v = { elex + 1, eley + 1 };
qu.push_back(v);
}
}
// Now if the end cell (i.e. bottom right cell)
// is 1(reachable) then we will send true.
return (rect[m - 1][n - 1] == 1);
}
// Driver Program
int main()
{
// Test case 1
int m1 = 5, n1 = 5, k1 = 2, r1 = 1;
vector<int> X1 = { 1, 3 };
vector<int> Y1 = { 3, 3 };
// Function call
if (isPossible(m1, n1, k1, r1, X1, Y1))
cout << "Possible" << endl;
else
cout << "Not Possible" << endl;
// Test case 2
int m2 = 5, n2 = 5, k2 = 2, r2 = 1;
vector<int> X2 = { 1, 1 };
vector<int> Y2 = { 2, 3 };
// Function call
if (isPossible(m2, n2, k2, r2, X2, Y2))
cout << "Possible" << endl;
else
cout << "Not Possible" << endl;
return 0;
}
Python3
# Python3 program to find out path in
# a rectangle containing circles.
import math
import queue
# Function to find out if there is
# any possible path or not.
def isPossible(m, n, k, r, X, Y):
# Take an array of m*n size and
# initialize each element to 0.
rect = [[0] * n for i in range(m)]
# Now using Pythagorean theorem find if a
# cell touches or within any circle or not.
for i in range(m):
for j in range(n):
for p in range(k):
if (math.sqrt((pow((X[p] - 1 - i), 2) +
pow((Y[p] - 1 - j), 2))) <= r):
rect[i][j] = -1
# If the starting cell comes within
# any circle return false.
if (rect[0][0] == -1):
return False
# Now use BFS to find if there
# is any possible path or not.
# Initialize the queue which holds
# the discovered cells whose neighbors
# are not discovered yet.
qu = queue.Queue()
rect[0][0] = 1
qu.put([0, 0])
# Discover cells until queue is not empty
while (not qu.empty()):
arr = qu.get()
elex = arr[0]
eley = arr[1]
# Discover the eight adjacent nodes.
# check top-left cell
if ((elex > 0) and (eley > 0) and
(rect[elex - 1][eley - 1] == 0)):
rect[elex - 1][eley - 1] = 1
v = [elex - 1, eley - 1]
qu.put(v)
# check top cell
if ((elex > 0) and
(rect[elex - 1][eley] == 0)):
rect[elex - 1][eley] = 1
v = [elex - 1, eley]
qu.put(v)
# check top-right cell
if ((elex > 0) and (eley < n - 1) and
(rect[elex - 1][eley + 1] == 0)):
rect[elex - 1][eley + 1] = 1
v = [elex - 1, eley + 1]
qu.put(v)
# check left cell
if ((eley > 0) and
(rect[elex][eley - 1] == 0)):
rect[elex][eley - 1] = 1
v = [elex, eley - 1]
qu.put(v)
# check right cell
if ((eley < n - 1) and
(rect[elex][eley + 1] == 0)):
rect[elex][eley + 1] = 1
v = [elex, eley + 1]
qu.put(v)
# check bottom-left cell
if ((elex < m - 1) and (eley > 0) and
(rect[elex + 1][eley - 1] == 0)):
rect[elex + 1][eley - 1] = 1
v = [elex + 1, eley - 1]
qu.put(v)
# check bottom cell
if ((elex < m - 1) and
(rect[elex + 1][eley] == 0)):
rect[elex + 1][eley] = 1
v = [elex + 1, eley]
qu.put(v)
# check bottom-right cell
if ((elex < m - 1) and (eley < n - 1) and
(rect[elex + 1][eley + 1] == 0)):
rect[elex + 1][eley + 1] = 1
v = [elex + 1, eley + 1]
qu.put(v)
# Now if the end cell (i.e. bottom right cell)
# is 1(reachable) then we will send true.
return (rect[m - 1][n - 1] == 1)
# Driver Code
if __name__ == '__main__':
# Test case 1
m1 = 5
n1 = 5
k1 = 2
r1 = 1
X1 = [1, 3]
Y1 = [3, 3]
# Function call
if (isPossible(m1, n1, k1, r1, X1, Y1)):
print("Possible")
else:
print("Not Possible")
# Test case 2
m2 = 5
n2 = 5
k2 = 2
r2 = 1
X2 = [1, 1]
Y2 = [2, 3]
# Function call
if (isPossible(m2, n2, k2, r2, X2, Y2)):
print("Possible")
else:
print("Not Possible")
# This code is contributed by PranchalK
Javascript
// JavaScript program to find out path in
// a rectangle containing circles
// program to implement queue data structure
// Creating a custom class Queued.
class Queued {
constructor() {
this.items = [];
}
// add element to the queue
enqueue(element) {
return this.items.push(element);
}
front(){
return this.items[0];
}
// remove element from the queue
dequeue() {
if(this.items.length > 0) {
return this.items.shift();
}
}
// view the last element
peek() {
return this.items[this.items.length - 1];
}
// check if the queue is empty
isEmpty(){
return this.items.length == 0;
}
// the size of the queue
size(){
return this.items.length;
}
// empty the queue
clear(){
this.items = [];
}
}
// Function to find out if there is
// any possible path or not.
function isPossible(m, n, k, r, X, Y)
{
// Take an array of m*n size and
// initialize each element to 0.
let rect = new Array(m);
for(let i = 0; i < m; i++){
let temp = new Array(n).fill(0);
rect[i] = temp;
}
// Now using Pythagorean theorem find if a
// cell touches or within any circle or not.
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
for (let p = 0; p < k; p++) {
if (Math.sqrt((Math.pow((X[p] - 1 - i), 2) + Math.pow((Y[p] - 1 - j), 2))) <= r) {
rect[i][j] = -1;
}
}
}
}
// If the starting cell comes within
// any circle return false.
if (rect[0][0] == -1){
return false;
}
// Now use BFS to find if there
// is any possible path or not.
// Initialize the queue which holds
// the discovered cells whose neighbors
// are not discovered yet.
let qu = new Queued();
rect[0][0] = 1;
qu.enqueue([0, 0]);
// Discover cells until queue is not empty
while (!qu.isEmpty()) {
let arr = qu.front();
qu.dequeue();
let elex = arr[0];
let eley = arr[1];
// Discover the eight adjacent nodes.
// check top-left cell
if ((elex > 0) && (eley > 0) && (rect[elex - 1][eley - 1] == 0)) {
rect[elex - 1][eley - 1] = 1;
let v = [elex - 1, eley - 1];
qu.enqueue(v);
}
// check top cell
if ((elex > 0) && (rect[elex - 1][eley] == 0)) {
rect[elex - 1][eley] = 1;
let v = [elex - 1, eley];
qu.enqueue(v);
}
// check top-right cell
if ((elex > 0) && (eley < n - 1)
&& (rect[elex - 1][eley + 1] == 0)) {
rect[elex - 1][eley + 1] = 1;
let v = [elex - 1, eley + 1];
qu.enqueue(v);
}
// check left cell
if ((eley > 0) && (rect[elex][eley - 1] == 0)) {
rect[elex][eley - 1] = 1;
let v = [elex, eley - 1];
qu.enqueue(v);
}
// check right cell
if ((eley < n - 1) && (rect[elex][eley + 1] == 0)) {
rect[elex][eley + 1] = 1;
let v = [elex, eley + 1];
qu.enqueue(v);
}
// check bottom-left cell
if ((elex < m - 1) && (eley > 0) && (rect[elex + 1][eley - 1] == 0)) {
rect[elex + 1][eley - 1] = 1;
let v = [elex + 1, eley - 1];
qu.enqueue(v);
}
// check bottom cell
if ((elex < m - 1) && (rect[elex + 1][eley] == 0)) {
rect[elex + 1][eley] = 1;
let v = [elex + 1, eley];
qu.enqueue(v);
}
// check bottom-right cell
if ((elex < m - 1) && (eley < n - 1) && (rect[elex + 1][eley + 1] == 0)) {
rect[elex + 1][eley + 1] = 1;
let v = [elex + 1, eley + 1];
qu.enqueue(v);
}
}
// Now if the end cell (i.e. bottom right cell)
// is 1(reachable) then we will send true.
return (rect[m - 1][n - 1] == 1);
}
// Driver Program
{
// Test case 1
let m1 = 5, n1 = 5, k1 = 2, r1 = 1;
let X1 = [1, 3];
let Y1 = [3, 3];
// Function call
if (isPossible(m1, n1, k1, r1, X1, Y1)){
console.log("Possible");
}
else{
console.log("Not Possible");
}
// Test case 2
let m2 = 5, n2 = 5, k2 = 2, r2 = 1;
let X2 = [1, 1];
let Y2 = [2, 3];
// Function call
if (isPossible(m2, n2, k2, r2, X2, Y2)){
console.log("Possible");
}
else{
console.log("Not Possible");
}
}
// The code is contributed by Nidhi goel
Possible Not Possible
Complejidad del tiempo: se necesita O (m * n * k) tiempo para calcular si una celda está dentro o no de un círculo. Y toma tiempo O (V + E) en BFS. Aquí, el número de aristas en la cuadrícula m*n es m*(n-1)+n*(m-1) y los vértices m*n. Entonces toma O (m * n) tiempo en DFS. Por lo tanto, la complejidad del tiempo es O(m*n*k). La complejidad se puede mejorar si iteramos a través de cada círculo y marcamos -1 las celdas que se encuentran dentro de él.
Espacio Auxiliar: O(nxm)
Sugiera si alguien tiene una mejor solución que sea más eficiente en términos de espacio y tiempo.
Este artículo es una contribución de Aarti_Rathi . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.