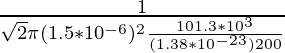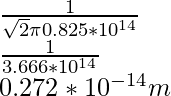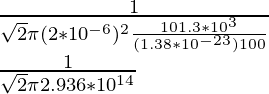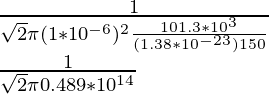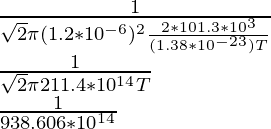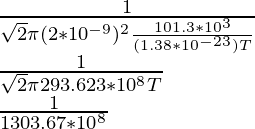Camino libre medio: definición, fórmula, derivación, ejemplos

Posted on by Rudeus Greyrat

La teoría cinética se introdujo para explicar la estructura y composición de las moléculas con respecto a las partículas submicroscópicas. La teoría habla del aumento de presión debido al constante movimiento y colisión de las partículas submicroscópicas. También analiza otras propiedades de un gas, como la temperatura, la presión, el volumen, la viscosidad, la difusión, la conductividad térmica, etc. La teoría desarrolla una relación entre las partículas microscópicas y las propiedades macroscópicas. Las moléculas de gas siempre están en constante movimiento y chocan entre sí y con las paredes del recipiente, en tal caso, es difícil e importante aprender la dinámica de los gases.

Naturaleza molecular de la materia

Como se sabe que hay tres formas de materia, son sólidos, líquidos y gases. Las moléculas de un sólido están estrechamente empaquetadas y tienen un espacio intermolecular mínimo entre ellas. En los líquidos, las moléculas están relativamente menos empaquetadas y, por lo tanto, tienen relativamente más espacio intermolecular entre ellas. Los gases, por otro lado, tienen moléculas empaquetadas muy sueltas y la distancia intermolecular entre ellas es mayor en comparación con los otros estados.

Ruta libre

Entendamos qué es un camino libre. Por definición, un camino libre es una distancia entre dos colisiones consecutivas. Como se sabe a través del comportamiento de los gases, las moléculas de un gas están siempre en constante movimiento. 

Chocan entre sí y con las paredes del contenedor. Supongamos que la molécula 1 choca primero con la molécula 2 y luego con la molécula 3 y así sucesivamente. Cuando la molécula 1 choca con la molécula 2, se conoce como la primera colisión. Cuando choca con la molécula 3, se conoce como segunda colisión, y así sucesivamente. 

La distancia entre la primera y la segunda colisión se conoce como el camino libre indicado como λ 1 , la distancia entre la segunda y la tercera colisión se conoce como λ 2 , y así sucesivamente. Dado que no hay colisión entre dos colisiones consecutivas cualesquiera, el camino se conoce como camino libre (λ 1 , λ 2 , λ 3 , etc.).

Camino libre medio

Camino libre medio

El camino libre medio es el camino promedio recorrido por las moléculas entre colisiones. Se sabe que existen diferentes caminos libres con diferentes longitudes de camino. A continuación se muestran los caminos libres, 

λ 1 = Primer camino libre

λ 2 = Segundo camino libre

λ 3 = Tercer camino libre

λ n = n-ésimo camino libre

El promedio de estas longitudes de camino se conoce como el camino libre medio. Por lo tanto, el camino libre medio puede (denotado por λ) calcularse como,

λ = (λ 1 + λ 2 + λ 3 + … λ norte )/ n

Fórmulas en camino libre medio

Tomemos el ejemplo de una sola molécula que tiene un diámetro d. Imaginándola moviéndose a través de otras moléculas, considerando que las otras moléculas están quietas y no chocando, la molécula recorre una cierta distancia en forma cilíndrica. El área de la sección transversal es πd2. El volumen del cilindro es πd2 × vt, donde v es la velocidad de la molécula y t es el tiempo. Consideremos que el número de moléculas por unidad de volumen es N/V. El camino libre medio se puede escribir como,

λ = Longitud del camino/ número de colisiones

\lambda=\dfrac{vt}{\pi d^2vt \frac{N}{V}}

\lambda=\dfrac{1}{\pi d^2 \frac{N}{V}}

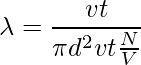
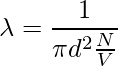
Ya que no se consideran las características de otras moléculas y las velocidades del numerador y del denominador son diferentes. La velocidad en el numerador es promedio y la velocidad en el denominador es relativa. Por lo tanto, se suma un factor de √2 al denominador.

\lambda=\dfrac{1}{\sqrt{2}\pi d^2 \frac{N}{V}}

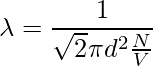
El tiempo entre dos colisiones sucesivas,

\tau=\dfrac{1}{nv\pi d^2}

La distancia media entre dos colisiones sucesivas,

l = \tau\times v =\dfrac{1}{n\pi d^2}

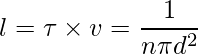
Problemas de muestra

Problema 1: encuentre el camino libre medio de la molécula de oxígeno que viaja en el aire a 200 K a 1 atm. El diámetro de la molécula de oxígeno es de 1,5 × 10 -6 m.

Solución:

Como ya se conoce la fórmula del camino libre medio, es decir,

λ = \frac{1}{\sqrt{2}\pi d^2 \frac{N}{V}}

N/V es la densidad numérica que se puede equiparar a P/KT por la ley de los gases ideales,

Por lo tanto,

λ = \frac{1}{\sqrt{2}\pi d^2 \frac{P}{KT}}

λ = \frac{1}{\sqrt{2}\pi (1,5*10^{-6})^2 \frac{101,3 * 10^3}{(1,38*10^{-23})200}}

λ = \frac{1}{\sqrt{2}\pi 0,825* 10^{14}}\\ \frac{1}{3,666*10^{14}}\\ 0,272*10^{-14}m

Problema 2: encuentre el camino libre medio de la molécula de oxígeno que viaja en el aire a 100 K a 1 atm. El diámetro de la molécula de oxígeno es 2 × 10 -6 m.

Solución:

Como ya se conoce la fórmula del camino libre medio, es decir,

λ = \frac{1}{\sqrt{2}\pi d^2 \frac{N}{V}}

N/V es la densidad numérica que se puede equiparar a P/KT por la ley de los gases ideales,

Por lo tanto,

λ = \frac{1}{\sqrt{2}\pi d^2 \frac{P}{KT}}

λ = \frac{1}{\sqrt{2}\pi (2*10^{-6})^2 \frac{101.3 * 10^3}{(1.38*10^{-23})100}}\\ \frac{1}{\sqrt{2}\pi 2.936 * 10^{14}}\\

λ = 0,076 × 10 -14

λ = 7,6 × 10 -16 m

Problema 3: encuentre el camino libre medio de la molécula de oxígeno que viaja en el aire a 150 K a 1 atm. El diámetro de la molécula de oxígeno es 1 × 10 -6 m.

Solución:

Como ya se conoce la fórmula del camino libre medio, es decir,

λ = \frac{1}{\sqrt{2}\pi d^2 \frac{N}{V}}

N/V es la densidad numérica que se puede equiparar a P/KT por la ley de los gases ideales,

Por lo tanto,

λ = \frac{1}{\sqrt{2}\pi d^2 \frac{P}{KT}}

λ = \frac{1}{\sqrt{2}\pi (1*10^{-6})^2 \frac{101.3 * 10^3}{(1.38*10^{-23})150}}\\ \frac{1}{\sqrt{2}\pi 0.489 * 10^{14}}\\

λ = 2,17 × 10 -14

λ = 2,17 × 10 -14 m

Problema 4: Si el camino libre medio de una molécula se da como 1,5 × 10 -10 m. Averigüe a qué temperatura en pascales se encuentra la molécula viajando a 2 atm cuando el diámetro de la molécula se da como 1,2 × 10 -6 m.

Solución:

Como ya se conoce la fórmula del camino libre medio, es decir,

λ = \frac{1}{\sqrt{2}\pi d^2 \frac{N}{V}}

N/V es la densidad numérica que se puede equiparar a P/KT por la ley de los gases ideales,

Por lo tanto,

λ = \frac{1}{\sqrt{2}\pi d^2 \frac{P}{KT}}

1,5 × 10 -10 = \frac{1}{\sqrt{2}\pi (1.2*10^{-6})^2 \frac{2*101.3 * 10^3}{(1.38*10^{-23})T}}\\ \frac{1}{\sqrt{2}\pi 211.4* 10^{14}T}\\ \frac{1}{938.606*10^{14}}

(1.5 × 10 -10 )(938.606 × 10 14 ) = 1/T

1407,909 × 10 4 = 1/T

T = 7,10 K

Problema 5: Si el camino libre medio de una molécula se da como 1 × 10 -6 m. Averigüe a qué temperatura en pascales está la molécula viajando a 1 atm cuando el diámetro de la molécula se da como 2 × 10 -9 m.

Solución:

Como ya se conoce la fórmula del camino libre medio, es decir,

λ = \frac{1}{\sqrt{2}\pi d^2 \frac{N}{V}}

N/V es la densidad numérica que se puede equiparar a P/KT por la ley de los gases ideales,

Por lo tanto,

λ = \frac{1}{\sqrt{2}\pi d^2 \frac{P}{KT}}

1 × 10 -6 = \frac{1}{\sqrt{2}\pi (2*10^{-9})^2 \frac{101.3 * 10^3}{(1.38*10^{-23})T}}\\ \frac{1}{\sqrt{2}\pi 293.623* 10^{8}T}\\ \frac{1}{1303.67*10^{8}}

(1 × 10 -6 )(1303.67 × 10 8 ) = 1/T

1303.67 × 10 2 = 1/T

T = 7,6 × 10 -6

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *