Inspección de ruta o cartero chino | Conjunto 1 (introducción)

El problema del cartero chino es una variación del problema del circuito euleriano para gráficos no dirigidos. Un circuito de Euler es un paseo cerrado que cubre todos los bordes una vez que la posición inicial y final es la misma. El problema del cartero chino se define para gráficos conectados y no dirigidos. El problema es encontrar la ruta o circuito más corto que visite cada borde del gráfico al menos una vez. 

Si el gráfico de entrada contiene el circuito de Euler, entonces una solución del problema es el circuito de Euler. 
Un gráfico conectado y no dirigido tiene un ciclo euleriano si » todos los vértices tienen un grado par «. 
 

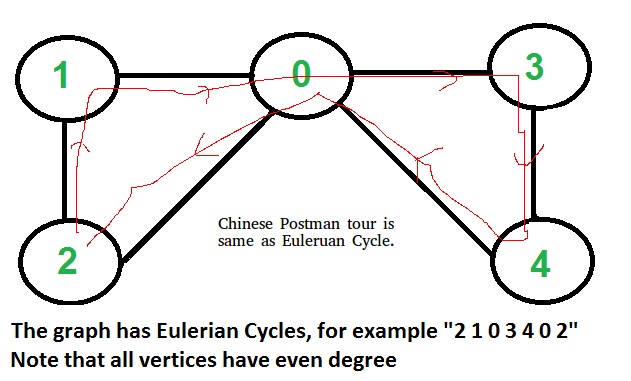
No importa si el gráfico está ponderado o no, la ruta del cartero chino siempre es igual que el circuito euleriano, si existe. En el gráfico ponderado, el peso mínimo posible de Postman Tour es la suma de todos los pesos de borde que obtenemos a través del circuito euleriano. No podemos obtener una ruta más corta ya que debemos visitar todos los bordes al menos una vez. 

  Si el gráfico de entrada NO contiene el circuito de Euler 

En este caso, la tarea se reduce a seguir. 

1) En gráfico no ponderado, número mínimo de aristas a duplicar para que el gráfico dado se convierta en un gráfico con Ciclo Euleriano. 

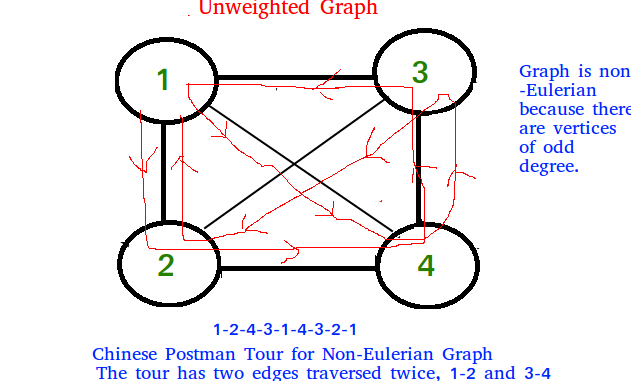
2) En el gráfico ponderado, el peso total mínimo de los bordes a duplicar para que el gráfico dado se convierta en un gráfico con Ciclo Euleriano.

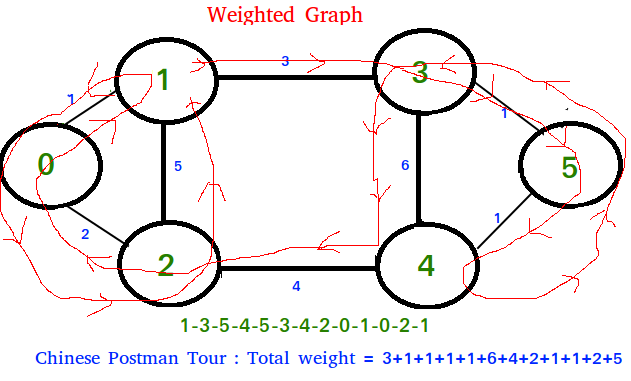
Algorithm to find shortest closed path or optimal 
Chinese postman route in a weighted graph that may
not be Eulerian.

step 1 : If graph is Eulerian, return sum of all 
         edge weights.Else do following steps.
step 2 : We find all the vertices with odd degree 
step 3 : List all possible pairings of odd vertices  
         For n odd vertices total number of pairings 
         possible are, (n-1) * (n-3) * (n -5)... * 1
step 4 : For each set of pairings, find the shortest 
         path connecting them.
step 5 : Find the pairing with minimum shortest path 
         connecting pairs.
step 6 : Modify the graph by adding all the edges that  
         have been found in step 5.
step 7 : Weight of Chinese Postman Tour is sum of all 
         edges in the modified graph.
step 8 : Print Euler Circuit of the modified graph. 
         This Euler Circuit is Chinese Postman Tour.   

Ilustración : 

               3
        (a)-----------------(b)
     1 /  |                  |  \1
      /   |                  |   \
     (c)  | 5               6|   (d)
      \   |                  |   /
     2 \  |         4        |  /1
        (e)------------------(f)
As we see above graph does not contain Eulerian circuit
because is has odd degree vertices [a, b, e, f]
they all are odd degree vertices . 

First we make all possible pairs of odd degree vertices
[ae, bf], [ab, ef], [af, eb] 
so pairs with min sum of weight are [ae, bf] :
ae = (ac + ce = 3 ),  bf = ( bd + df = 2 ) 
Total : 5

We add edges ac, ce, bd and df to the original graph and
create a modified graph.

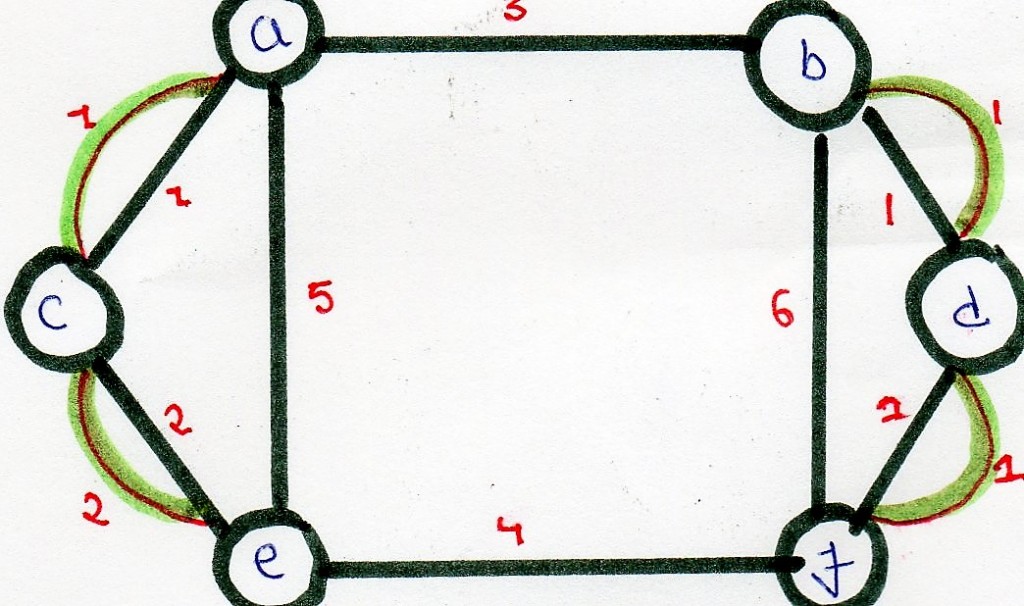
Optimal chinese postman route is of length : 5 + 23 = 
28 [ 23 = sum  of all edges of modified graph ]

Chinese Postman Route :  
a - b - d - f - d - b - f - e - c - a - c - e - a 
This route is Euler Circuit of the modified graph. 

Este artículo es una contribución de Nishant Singh . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.