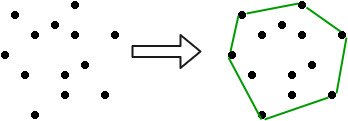
Un casco convexo es el polígono convexo más pequeño que contiene todos los puntos dados.
La entrada es una array de puntos especificados por sus coordenadas x e y. La salida es el casco convexo de este conjunto de puntos. Ejemplos:
Input : points[] = {(0, 0), (0, 4), (-4, 0), (5, 0),
(0, -6), (1, 0)};
Output : (-4, 0), (5, 0), (0, -6), (0, 4)
Requisito previo: Tangentes entre dos polígonos convexos Algoritmo: Dado el conjunto de puntos para los que tenemos que encontrar la envolvente convexa. Supongamos que conocemos el casco convexo de los medios puntos izquierdos y los medios puntos derechos, entonces el problema ahora es fusionar estos dos cascos convexos y determinar el casco convexo para el conjunto completo. Esto se puede hacer encontrando la tangente superior e inferior a los cascos convexos derecho e izquierdo. Esto se ilustra aquí Tangentes entre dos polígonos convexos Sean a la envolvente convexa izquierda y b la envolvente convexa derecha. Luego, las tangentes inferior y superior se nombran como 1 y 2 respectivamente, como se muestra en la figura. Luego, el contorno rojo muestra el casco convexo final. Ahora queda el problema, cómo encontrar el casco convexo para la mitad izquierda y derecha. Ahora entra en escena la recursividad, dividimos el conjunto de puntos hasta que el número de puntos en el conjunto sea muy pequeño, digamos 5, y podemos encontrar la envolvente convexa para estos puntos mediante el algoritmo bruto. La fusión de estas mitades daría como resultado el casco convexo para el conjunto completo de puntos. Nota: Hemos usado el algoritmo bruto para encontrar el casco convexo para una pequeña cantidad de puntos y tiene una complejidad de tiempo de
Ahora queda el problema, cómo encontrar el casco convexo para la mitad izquierda y derecha. Ahora entra en escena la recursividad, dividimos el conjunto de puntos hasta que el número de puntos en el conjunto sea muy pequeño, digamos 5, y podemos encontrar la envolvente convexa para estos puntos mediante el algoritmo bruto. La fusión de estas mitades daría como resultado el casco convexo para el conjunto completo de puntos. Nota: Hemos usado el algoritmo bruto para encontrar el casco convexo para una pequeña cantidad de puntos y tiene una complejidad de tiempo de ![]() . Pero algunas personas sugieren lo siguiente, el casco convexo para 3 puntos o menos es el conjunto completo de puntos. Esto es correcto, pero el problema surge cuando intentamos fusionar un casco convexo izquierdo de 2 puntos y un casco convexo derecho de 3 puntos, entonces el programa queda atrapado en un bucle infinito en algunos casos especiales. Entonces, para deshacerme de este problema, encontré directamente el casco convexo para 5 o menos puntos por
. Pero algunas personas sugieren lo siguiente, el casco convexo para 3 puntos o menos es el conjunto completo de puntos. Esto es correcto, pero el problema surge cuando intentamos fusionar un casco convexo izquierdo de 2 puntos y un casco convexo derecho de 3 puntos, entonces el programa queda atrapado en un bucle infinito en algunos casos especiales. Entonces, para deshacerme de este problema, encontré directamente el casco convexo para 5 o menos puntos por ![]() algoritmo, que es algo mayor pero no afecta la complejidad general del algoritmo.
algoritmo, que es algo mayor pero no afecta la complejidad general del algoritmo.
CPP
// A divide and conquer program to find convex
// hull of a given set of points.
#include<bits/stdc++.h>
using namespace std;
// stores the centre of polygon (It is made
// global because it is used in compare function)
pair<int, int> mid;
// determines the quadrant of a point
// (used in compare())
int quad(pair<int, int> p)
{
if (p.first >= 0 && p.second >= 0)
return 1;
if (p.first <= 0 && p.second >= 0)
return 2;
if (p.first <= 0 && p.second <= 0)
return 3;
return 4;
}
// Checks whether the line is crossing the polygon
int orientation(pair<int, int> a, pair<int, int> b,
pair<int, int> c)
{
int res = (b.second-a.second)*(c.first-b.first) -
(c.second-b.second)*(b.first-a.first);
if (res == 0)
return 0;
if (res > 0)
return 1;
return -1;
}
// compare function for sorting
bool compare(pair<int, int> p1, pair<int, int> q1)
{
pair<int, int> p = make_pair(p1.first - mid.first,
p1.second - mid.second);
pair<int, int> q = make_pair(q1.first - mid.first,
q1.second - mid.second);
int one = quad(p);
int two = quad(q);
if (one != two)
return (one < two);
return (p.second*q.first < q.second*p.first);
}
// Finds upper tangent of two polygons 'a' and 'b'
// represented as two vectors.
vector<pair<int, int>> merger(vector<pair<int, int> > a,
vector<pair<int, int> > b)
{
// n1 -> number of points in polygon a
// n2 -> number of points in polygon b
int n1 = a.size(), n2 = b.size();
int ia = 0, ib = 0;
for (int i=1; i<n1; i++)
if (a[i].first > a[ia].first)
ia = i;
// ib -> leftmost point of b
for (int i=1; i<n2; i++)
if (b[i].first < b[ib].first)
ib=i;
// finding the upper tangent
int inda = ia, indb = ib;
bool done = 0;
while (!done)
{
done = 1;
while (orientation(b[indb], a[inda], a[(inda+1)%n1]) >=0)
inda = (inda + 1) % n1;
while (orientation(a[inda], b[indb], b[(n2+indb-1)%n2]) <=0)
{
indb = (n2+indb-1)%n2;
done = 0;
}
}
int uppera = inda, upperb = indb;
inda = ia, indb=ib;
done = 0;
int g = 0;
while (!done)//finding the lower tangent
{
done = 1;
while (orientation(a[inda], b[indb], b[(indb+1)%n2])>=0)
indb=(indb+1)%n2;
while (orientation(b[indb], a[inda], a[(n1+inda-1)%n1])<=0)
{
inda=(n1+inda-1)%n1;
done=0;
}
}
int lowera = inda, lowerb = indb;
vector<pair<int, int>> ret;
//ret contains the convex hull after merging the two convex hulls
//with the points sorted in anti-clockwise order
int ind = uppera;
ret.push_back(a[uppera]);
while (ind != lowera)
{
ind = (ind+1)%n1;
ret.push_back(a[ind]);
}
ind = lowerb;
ret.push_back(b[lowerb]);
while (ind != upperb)
{
ind = (ind+1)%n2;
ret.push_back(b[ind]);
}
return ret;
}
// Brute force algorithm to find convex hull for a set
// of less than 6 points
vector<pair<int, int>> bruteHull(vector<pair<int, int>> a)
{
// Take any pair of points from the set and check
// whether it is the edge of the convex hull or not.
// if all the remaining points are on the same side
// of the line then the line is the edge of convex
// hull otherwise not
set<pair<int, int> >s;
for (int i=0; i<a.size(); i++)
{
for (int j=i+1; j<a.size(); j++)
{
int x1 = a[i].first, x2 = a[j].first;
int y1 = a[i].second, y2 = a[j].second;
int a1 = y1-y2;
int b1 = x2-x1;
int c1 = x1*y2-y1*x2;
int pos = 0, neg = 0;
for (int k=0; k<a.size(); k++)
{
if (a1*a[k].first+b1*a[k].second+c1 <= 0)
neg++;
if (a1*a[k].first+b1*a[k].second+c1 >= 0)
pos++;
}
if (pos == a.size() || neg == a.size())
{
s.insert(a[i]);
s.insert(a[j]);
}
}
}
vector<pair<int, int>>ret;
for (auto e:s)
ret.push_back(e);
// Sorting the points in the anti-clockwise order
mid = {0, 0};
int n = ret.size();
for (int i=0; i<n; i++)
{
mid.first += ret[i].first;
mid.second += ret[i].second;
ret[i].first *= n;
ret[i].second *= n;
}
sort(ret.begin(), ret.end(), compare);
for (int i=0; i<n; i++)
ret[i] = make_pair(ret[i].first/n, ret[i].second/n);
return ret;
}
// Returns the convex hull for the given set of points
vector<pair<int, int>> divide(vector<pair<int, int>> a)
{
// If the number of points is less than 6 then the
// function uses the brute algorithm to find the
// convex hull
if (a.size() <= 5)
return bruteHull(a);
// left contains the left half points
// right contains the right half points
vector<pair<int, int>>left, right;
for (int i=0; i<a.size()/2; i++)
left.push_back(a[i]);
for (int i=a.size()/2; i<a.size(); i++)
right.push_back(a[i]);
// convex hull for the left and right sets
vector<pair<int, int>>left_hull = divide(left);
vector<pair<int, int>>right_hull = divide(right);
// merging the convex hulls
return merger(left_hull, right_hull);
}
// Driver code
int main()
{
vector<pair<int, int> > a;
a.push_back(make_pair(0, 0));
a.push_back(make_pair(1, -4));
a.push_back(make_pair(-1, -5));
a.push_back(make_pair(-5, -3));
a.push_back(make_pair(-3, -1));
a.push_back(make_pair(-1, -3));
a.push_back(make_pair(-2, -2));
a.push_back(make_pair(-1, -1));
a.push_back(make_pair(-2, -1));
a.push_back(make_pair(-1, 1));
int n = a.size();
// sorting the set of points according
// to the x-coordinate
sort(a.begin(), a.end());
vector<pair<int, int> >ans = divide(a);
cout << "convex hull:\n";
for (auto e:ans)
cout << e.first << " "
<< e.second << endl;
return 0;
}
Producción:
Convex Hull: -5 -3 -1 -5 1 -4 0 0 -1 1
Complejidad de tiempo: la fusión de los cascos convexos izquierdo y derecho toma O (n) tiempo y como estamos dividiendo los puntos en dos partes iguales, la complejidad de tiempo del algoritmo anterior es O (n * log n).
Espacio Auxiliar: O(n)
Artículos relacionados :
- Casco convexo | Conjunto 1 (Algoritmo de Jarvis o Wrapping)
- Casco convexo | Juego 2 (escaneo de Graham)
- Algoritmo Quickhull para casco convexo
Este artículo es una contribución de Aarti_Rathi y Amritya Vagmi y le gustaría contribuir, también puede escribir un artículo usando write.geeksforgeeks.org o enviar su artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA