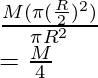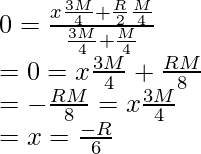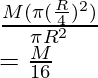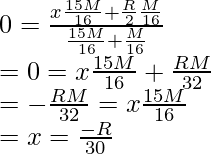Centro de masa

El centro de masa es una parte muy integral de la mecánica. Nos permite realizar cálculos sobre cuerpos grandes considerándolos como objetos puntuales. Estas simplificaciones luego se convirtieron en la base para el desarrollo de los diferentes campos de la mecánica. Por ejemplo, mecánica rotacional, mecánica gravitacional, etc. El Centro de masa intuitivamente significa el punto desde el cual podemos apoyar el objeto desde abajo. Por ejemplo, un palo se puede sostener desde un punto medio para que no se caiga. Del mismo modo, cada objeto tiene un punto similar. Esto se llama el Centro de masa .

Se pueden simplificar muchos problemas si se supone que la masa del objeto se encuentra en un punto en particular. Si se elige la posición correcta, las ecuaciones de fuerzas y movimiento se comportan de la misma manera que si se aplicaran cuando la masa se distribuye. Esta ubicación especial se denomina el Centro de Masa .

Su posición se define en relación con un objeto o el sistema de objetos cuyo centro de masa se va a calcular. Por lo general, para formas uniformes, es su centroide. Comencemos con formas simples y veamos dónde se encuentran sus centros de masas. Considere las formas dadas en la siguiente figura. Es fácil adivinar el centro de masas de las siguientes formas. Para la mayoría de ellos, el centro de masa está en su centroide.

Observe, para un anillo, su Centro de masa se encuentra dentro del anillo, lo que significa que es necesario que el Centro de masa de un cuerpo se encuentre en el propio cuerpo.

Encontrar el centro de masa

Ahora, es claro que los cuerpos que son uniformes y simétricos tienen su Centro de masas en su baricentro. Pero para cuerpos que no son simétricos y uniformes, la respuesta no es tan simple. El centro de masa de tales cuerpos puede estar en cualquier lugar. Calcular el centro de masa de un objeto complejo. Se toma un promedio ponderado de las ubicaciones de cada masa del cuerpo.

Digamos que hay un cuerpo que consta de un conjunto de masas «m _i «, cada una en la posición r _i, la ubicación del centro de masa r _cm está dada por la siguiente fórmula.

Señor _cm = metro ₁ r ₁ + metro ₂ r ₂ + ….

⇒ r _cm = $\frac{ m_1r_1 + m_2r_2 + ...}{M}$

En este caso, M = $\sum m_i$ , que es la masa total del cuerpo.

La técnica anterior utiliza aritmética vectorial. Para evitar la aritmética vectorial, podemos encontrar el centro de masa del cuerpo a lo largo del eje x y el eje y respectivamente. Las fórmulas para este caso se dan a continuación:

_cm x = $\frac{ m_1x_1 + m_2x_2 + ...}{M}$

y _cm = $\frac{ m_1y_1 + m_2y_2 + ...}{M}$

Centro de gravedad

Por lo general, se supone que la gravedad es una fuerza uniforme que actúa sobre el cuerpo. El centro de gravedad es el punto en el que se supone que la gravedad actúa sobre el cuerpo. El Centro de gravedad está por lo tanto en el mismo lugar que el Centro de masa. En la literatura de física, los términos Centro de gravedad y Centro de masa se usan indistintamente. Quieren decir lo mismo.

Fórmulas importantes del centro de masa

Algunos sistemas ocurren con más frecuencia en la vida real que otros. Al calcular el centro de masa para tales sistemas, el método tradicional lleva tiempo. Ciertas fórmulas del Centro de masa deben tenerse en cuenta al resolver las preguntas relacionadas con el Centro de masa. Estas fórmulas ayudan a simplificar los cálculos.

1. Sistema de dos masas puntuales

En tal sistema, COM se encuentra más cerca de la masa más pesada.

metro ₁ r ₁ = metro ₂ r ₂

Distancia de COM desde la masa m ₁ = $\frac{m_2r}{m_1 + m_2}$

Distancia de COM desde la masa m ₂ = $\frac{m_1r}{m_1 + m_2}$

2. Triángulo equilátero

El centro de masa se encuentra en el baricentro, que está a la altura de $\frac{h}{3}$

3. Disco semicircular

y _c = $\frac{ 4r}{3\pi}$

4. Anillo semicircular

y _c = $\frac{ 2r}{\pi}$

Veamos algunos problemas de muestra.

Problemas de muestra

Pregunta 1: Dos masas puntuales, m ₁ = 5 kg y m ₂ = 2 kg, están ubicadas en x = 2 m yx = 6 m respectivamente. Encuentre el centro de masa.

Solución:

La fórmula para el centro de masa está dada por,

_cm x = $\frac{ m_1x_1 + m_2x_2 + ...}{M}$

m ₁ = 5 kg, m ₂ = 2 kg y x = 2 m y x = 6 m.

M =m ₁ +m ₂

⇒ METRO = 5 + 2 = 7

_cm x = $\frac{ m_1x_1 + m_2x_2 + ...}{M}$

⇒x _cm = $\frac{ m_1x_1 + m_2x_2}{M}$

⇒x _cm = $\frac{ (5)(2) + (2)(6)}{7}$

⇒x _cm = $\frac{22}{7}$

Pregunta 2: dos masas puntuales, m ₁ = 5 kg y m ₂ = 2 kg, están ubicadas en y = 10 my y = -5 m respectivamente. Encuentre el centro de masa.

Solución:

La fórmula para el centro de masa está dada por,

_ycm = $\frac{ m_1y_1 + m_2y_2 + ...}{M}$

m ₁ = 5Kg, m ₂ = 2Kg y y = 10m y y = -5 m.

METRO = metro _{1 +} metro ₂

⇒ METRO = 5 + 2 = 7

y _cm = $\frac{ m_1y_1 + m_2y_2 + ...}{M}$

⇒ y _cm = $\frac{ m_1y_1 + m_2y_2}{M}$

⇒ y _cm = $\frac{ (5)(10) + (2)(-5)}{7}$

⇒ y _cm = $\frac{40}{7}$

Pregunta 3: dos masas puntuales, m ₁ = 1 kg y m ₂ = 2 kg, están ubicadas en el vector a = 6i + 4j y el vector b = -5i + 2j respectivamente. Encuentre el centro de masa.

Solución:

La fórmula para el centro de masa en la notación vectorial está dada por,

cm = _{_} $\frac{ m_1\vec{r_1} + m_2\vec{r_2} + ...}{M}$

m ₁ = 1Kg, m ₂ = 2Kg y a = 6i + 4j, b = -5i + 2j

METRO = metro _{1 +} metro ₂

⇒ METRO = 1 + 2 = 3

cm = _{_} $\frac{ m_1\vec{r_1} + m_2\vec{r_2} + ...}{M}$

⇒r _cm = $\frac{ m_1\vec{a} + m_2\vec{b}}{M}$

⇒ r _cm = $\frac{ (1)(6\hat{i} + 4\hat{j} ) + (2)(-5\hat{i} + 2\hat{j})}{7}$

⇒ r _cm = $\frac{ 6\hat{i} + 4\hat{j} + -10\hat{i} + 4\hat{j})}{7}$

⇒ r _cm = $\frac{ -4\hat{i} + 8\hat{j} }{7}$

Pregunta 4: dos masas puntuales, m ₁ = 4 kg y m ₂ = 2 kg, están ubicadas en el vector a = i + j y el vector b = -i + j respectivamente. Encuentre el centro de masa.

Solución:

La fórmula para el centro de masa en la notación vectorial está dada por,

cm = _{_} $\frac{ m_1\vec{r_1} + m_2\vec{r_2} + ...}{M}$

m ₁ = 4Kg, m ₂ = 2Kg y a = i + j, b = -i + j

METRO = metro _{1 +} metro ₂

⇒ METRO = 4 + 2 = 6

cm = _{_} $\frac{ m_1\vec{r_1} + m_2\vec{r_2} + ...}{M}$

⇒r _cm = $\frac{ m_1\vec{a} + m_2\vec{b}}{M}$

⇒ r _cm = $\frac{ (4)(\hat{i} + \hat{j} ) + (2)(\hat{i} -\hat{j})}{7}$

⇒ r _cm = $\frac{ 4\hat{i} + 4\hat{j} + 2\hat{i} -2\hat{j})}{7}$

⇒ r _cm = $\frac{ 6\hat{i} + 2\hat{j} }{7}$

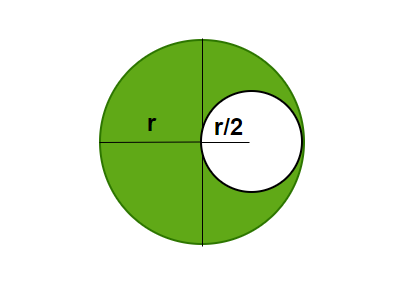
Pregunta 5: Un disco de radio R/2 se quita de un disco más grande de masa M de radio R. Encuentra el centro de masa.

Solución:

Dado que la densidad del disco es uniforme, el peso se distribuye uniformemente en toda el área.

Masa “m” del disco extraído = $\frac{M (\pi (\frac{R}{2})^2)}{\pi R^2} \\ = \frac{M}{4}$

Figura

La figura muestra el centro de masas de la parte restante y la parte eliminada. Tenga en cuenta que si ambos se toman juntos, el centro de masa debe estar en el Centro. Deje que la distancia del centro de masa de la porción restante sea «x».

$0 = \frac{x\frac{3M}{4} + \frac{R}{2}\frac{M}{4}}{\frac{3M}{4} + \frac{M}{4}} \\ = 0 = x\frac{3M}{4} + \frac{RM}{8} \\ = -\frac{RM}{8} = x\frac{3M}{4} \\ = x = \frac{-R}{6}$

Pregunta 6: A un disco mayor de masa M de radio R se le quita un disco de radio R/4, de la misma forma que en la figura anterior. Encuentre el centro de masa.

Solución:

Dado que la densidad del disco es uniforme, el peso se distribuye uniformemente en toda el área.

Masa “m” del disco extraído = $\frac{M (\pi (\frac{R}{4})^2)}{\pi R^2} \\ = \frac{M}{16}$

La figura muestra el centro de masas de la parte restante y la parte eliminada. Tenga en cuenta que si ambos se toman juntos, el centro de masa debe estar en el Centro. Deje que la distancia del centro de masa de la porción restante sea «x».

$0 = \frac{x\frac{15M}{16} + \frac{R}{2}\frac{M}{16}}{\frac{15M}{16} + \frac{M}{16}} \\ = 0 = x\frac{15M}{16} + \frac{RM}{32} \\ = -\frac{RM}{32} = x\frac{15M}{16} \\ = x = \frac{-R}{30}$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Centro de masa

Encontrar el centro de masa

Problemas de muestra

Deja una respuesta Cancelar la respuesta