Dado un gráfico no dirigido y conectado y un número n, cuente el número total de ciclos de longitud n en el gráfico. Un ciclo de longitud n simplemente significa que el ciclo contiene n vértices y n aristas. Y tenemos que contar todos esos ciclos que existen.
Ejemplo :
Input : n = 4
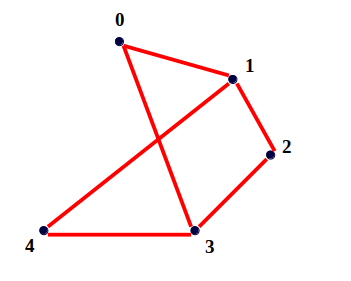
Output : Total cycles = 3 Explanation : Following 3 unique cycles 0 -> 1 -> 2 -> 3 -> 0 0 -> 1 -> 4 -> 3 -> 0 1 -> 2 -> 3 -> 4 -> 1 Note* : There are more cycles but these 3 are unique as 0 -> 3 -> 2 -> 1 -> 0 and 0 -> 1 -> 2 -> 3 -> 0 are same cycles and hence will be counted as 1.
Para resolver este problema, DFS (búsqueda primero en profundidad) se puede utilizar de manera efectiva. Usando DFS, encontramos todas las rutas posibles de longitud (n-1) para una fuente particular (o punto de partida). Luego verificamos si este camino termina con el vértice en el que comenzó, si es así, contamos esto como el ciclo de longitud n. Tenga en cuenta que buscamos la ruta de longitud (n-1) porque el borde n será el borde de cierre del ciclo.
Cada ruta posible de longitud (n-1) se puede buscar usando solo V – ( n – 1 ) vértices (donde V es el número total de vértices).
Para el ejemplo anterior, todos los ciclos de longitud 4 se pueden buscar usando solo 5-(4-1) = 2 vértices. La razón detrás de esto es bastante simple, porque buscamos todos los caminos posibles de longitud (n-1) = 3 usando estos 2 vértices que incluyen los 3 vértices restantes. Entonces, estos 2 vértices también cubren los ciclos de los 3 vértices restantes, y usando solo 3 vértices no podemos formar un ciclo de longitud 4 de todos modos.
Una cosa más a tener en cuenta es que cada vértice encuentra 2 ciclos duplicados por cada ciclo que forma. Para el ejemplo anterior, el vértice 0 encuentra dos ciclos duplicados, a saber , 0 -> 3 -> 2 -> 1 -> 0 y 0 -> 1 -> 2 -> 3 -> 0 . Por lo tanto, el conteo total debe dividirse por 2 porque cada ciclo se cuenta dos veces.
Implementación:
C++
// CPP Program to count cycles of length n
// in a given graph.
#include <bits/stdc++.h>
using namespace std;
// Number of vertices
const int V = 5;
void DFS(bool graph[][V], bool marked[], int n,
int vert, int start, int &count)
{
// mark the vertex vert as visited
marked[vert] = true;
// if the path of length (n-1) is found
if (n == 0) {
// mark vert as un-visited to make
// it usable again.
marked[vert] = false;
// Check if vertex vert can end with
// vertex start
if (graph[vert][start])
{
count++;
return;
} else
return;
}
// For searching every possible path of
// length (n-1)
for (int i = 0; i < V; i++)
if (!marked[i] && graph[vert][i])
// DFS for searching path by decreasing
// length by 1
DFS(graph, marked, n-1, i, start, count);
// marking vert as unvisited to make it
// usable again.
marked[vert] = false;
}
// Counts cycles of length N in an undirected
// and connected graph.
int countCycles(bool graph[][V], int n)
{
// all vertex are marked un-visited initially.
bool marked[V];
memset(marked, 0, sizeof(marked));
// Searching for cycle by using v-n+1 vertices
int count = 0;
for (int i = 0; i < V - (n - 1); i++) {
DFS(graph, marked, n-1, i, i, count);
// ith vertex is marked as visited and
// will not be visited again.
marked[i] = true;
}
return count/2;
}
int main()
{
bool graph[][V] = {{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0}};
int n = 4;
cout << "Total cycles of length " << n << " are "
<< countCycles(graph, n);
return 0;
}
Java
// Java program to calculate cycles of
// length n in a given graph
public class Main {
// Number of vertices
public static final int V = 5;
static int count = 0;
static void DFS(int graph[][], boolean marked[],
int n, int vert, int start) {
// mark the vertex vert as visited
marked[vert] = true;
// if the path of length (n-1) is found
if (n == 0) {
// mark vert as un-visited to
// make it usable again
marked[vert] = false;
// Check if vertex vert end
// with vertex start
if (graph[vert][start] == 1) {
count++;
return;
} else
return;
}
// For searching every possible
// path of length (n-1)
for (int i = 0; i < V; i++)
if (!marked[i] && graph[vert][i] == 1)
// DFS for searching path by
// decreasing length by 1
DFS(graph, marked, n-1, i, start);
// marking vert as unvisited to make it
// usable again
marked[vert] = false;
}
// Count cycles of length N in an
// undirected and connected graph.
static int countCycles(int graph[][], int n) {
// all vertex are marked un-visited
// initially.
boolean marked[] = new boolean[V];
// Searching for cycle by using
// v-n+1 vertices
for (int i = 0; i < V - (n - 1); i++) {
DFS(graph, marked, n-1, i, i);
// ith vertex is marked as visited
// and will not be visited again
marked[i] = true;
}
return count / 2;
}
// driver code
public static void main(String[] args) {
int graph[][] = {{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0}};
int n = 4;
System.out.println("Total cycles of length "+
n + " are "+
countCycles(graph, n));
}
}
// This code is contributed by nuclode
Python3
# Python Program to count
# cycles of length n
# in a given graph.
# Number of vertices
V = 5
def DFS(graph, marked, n, vert, start, count):
# mark the vertex vert as visited
marked[vert] = True
# if the path of length (n-1) is found
if n == 0:
# mark vert as un-visited to make
# it usable again.
marked[vert] = False
# Check if vertex vert can end with
# vertex start
if graph[vert][start] == 1:
count = count + 1
return count
else:
return count
# For searching every possible path of
# length (n-1)
for i in range(V):
if marked[i] == False and graph[vert][i] == 1:
# DFS for searching path by decreasing
# length by 1
count = DFS(graph, marked, n-1, i, start, count)
# marking vert as unvisited to make it
# usable again.
marked[vert] = False
return count
# Counts cycles of length
# N in an undirected
# and connected graph.
def countCycles( graph, n):
# all vertex are marked un-visited initially.
marked = [False] * V
# Searching for cycle by using v-n+1 vertices
count = 0
for i in range(V-(n-1)):
count = DFS(graph, marked, n-1, i, i, count)
# ith vertex is marked as visited and
# will not be visited again.
marked[i] = True
return int(count/2)
# main :
graph = [[0, 1, 0, 1, 0],
[1 ,0 ,1 ,0, 1],
[0, 1, 0, 1, 0],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 0]]
n = 4
print("Total cycles of length ",n," are ",countCycles(graph, n))
# this code is contributed by Shivani Ghughtyal
C#
// C# program to calculate cycles of
// length n in a given graph
using System;
class GFG
{
// Number of vertices
public static int V = 5;
static int count = 0;
static void DFS(int [,]graph, bool []marked,
int n, int vert, int start)
{
// mark the vertex vert as visited
marked[vert] = true;
// if the path of length (n-1) is found
if (n == 0)
{
// mark vert as un-visited to
// make it usable again
marked[vert] = false;
// Check if vertex vert end
// with vertex start
if (graph[vert, start] == 1)
{
count++;
return;
}
else
return;
}
// For searching every possible
// path of length (n-1)
for (int i = 0; i < V; i++)
if (!marked[i] && graph[vert, i] == 1)
// DFS for searching path by
// decreasing length by 1
DFS(graph, marked, n - 1, i, start);
// marking vert as unvisited to make it
// usable again
marked[vert] = false;
}
// Count cycles of length N in an
// undirected and connected graph.
static int countCycles(int [,]graph, int n)
{
// all vertex are marked un-visited
// initially.
bool []marked = new bool[V];
// Searching for cycle by using
// v-n+1 vertices
for (int i = 0; i < V - (n - 1); i++)
{
DFS(graph, marked, n - 1, i, i);
// ith vertex is marked as visited
// and will not be visited again
marked[i] = true;
}
return count / 2;
}
// Driver code
public static void Main()
{
int [,]graph = {{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 0}};
int n = 4;
Console.WriteLine("Total cycles of length "+
n + " are "+
countCycles(graph, n));
}
}
/* This code contributed by PrinciRaj1992 */
Javascript
<script>
// JavaScript program to calculate cycles of
// length n in a given graph
// Number of vertices
var V = 5;
var count = 0;
function DFS(graph, marked, n, vert, start)
{
// mark the vertex vert as visited
marked[vert] = true;
// if the path of length (n-1) is found
if (n == 0)
{
// mark vert as un-visited to
// make it usable again
marked[vert] = false;
// Check if vertex vert end
// with vertex start
if (graph[vert][start] == 1)
{
count++;
return;
}
else
return;
}
// For searching every possible
// path of length (n-1)
for (var i = 0; i < V; i++)
if (!marked[i] && graph[vert][i] == 1)
// DFS for searching path by
// decreasing length by 1
DFS(graph, marked, n - 1, i, start);
// marking vert as unvisited to make it
// usable again
marked[vert] = false;
}
// Count cycles of length N in an
// undirected and connected graph.
function countCycles(graph, n)
{
// all vertex are marked un-visited
// initially.
var marked = Array(V).fill(false);
// Searching for cycle by using
// v-n+1 vertices
for (var i = 0; i < V - (n - 1); i++)
{
DFS(graph, marked, n - 1, i, i);
// ith vertex is marked as visited
// and will not be visited again
marked[i] = true;
}
return parseInt(count / 2);
}
// Driver code
var graph = [[0, 1, 0, 1, 0],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 0],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 0]];
var n = 4;
document.write("Total cycles of length "+
n + " are "+
countCycles(graph, n));
</script>
Total cycles of length 4 are 3
Este artículo es una contribución de Shubham Rana . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA