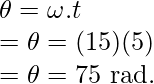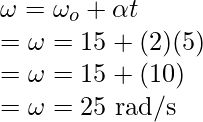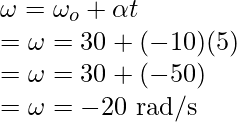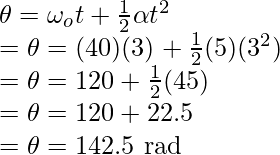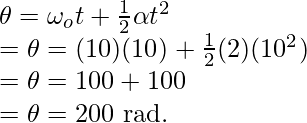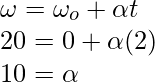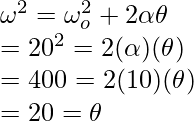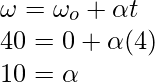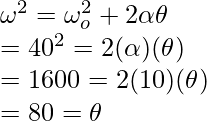Cinemática del movimiento de rotación

No es difícil notar la naturaleza análoga del movimiento de rotación y el movimiento cinemático. Los términos de velocidad angular y aceleración angular nos recuerdan la velocidad y la aceleración lineales. Entonces, similar a la ecuación cinemática de movimiento. También se pueden definir ecuaciones de movimiento de rotación. Tales ecuaciones nos ayudan a calcular parámetros como el ángulo de rotación y la velocidad angular. Miremos estas ecuaciones y veamos cómo se pueden usar en un contexto similar.

Cinemática del movimiento de rotación

Cantidades rotacionales tales como ángulo, velocidad angular y aceleración angular. Veamos cómo se relaciona la ecuación de movimiento con las ecuaciones de movimiento de rotación. Considere una rueda que comienza a girar con aceleración angular y cubre muchas revoluciones. En términos de la notación formal, se puede decir que una rueda que tiene un gran finaliza girando en un gran ángulo a través de un número de revoluciones (. Esta situación es similar a un vehículo que se mueve en una carretera con cierta aceleración y alcanza cierta velocidad. Estos parámetros se pueden calcular usando la cinemática del movimiento lineal. Se puede usar un enfoque similar en el movimiento de rotación. Estas ecuaciones se denominan ecuaciones cinemáticas del movimiento de rotación. La siguiente tabla representa algunas cantidades análogas.

Rotacional	traslacional
v
s
a
θ = ωt	s = vt

Ecuaciones Cinemáticas de Movimiento

Para un objeto que se mueve con una aceleración «a». Digamos que el tiempo se denota por “t”, la velocidad actual por “v”, la velocidad inicial por “u” y la distancia recorrida por el objeto por “s”. Las ecuaciones que gobiernan este movimiento se dan a continuación. Tenga en cuenta que estas ecuaciones son solo para situaciones en las que la aceleración «a» es constante y el objeto se mueve en línea recta.

v = tu + en

$s = ut + \frac{1}{2}at^2$

v ² = tu ² + 2 como

Ahora, en el caso del movimiento de rotación, la velocidad (v) corresponde a la velocidad angular(). El desplazamiento “s” es análogo al ángulo de rotate(), la aceleración(a) es análoga a la aceleración angular().

Ecuaciones cinemáticas para el movimiento de rotación

Para un objeto que gira con una aceleración angular, digamos que el tiempo se denota con “t”, la velocidad angular actual con , la velocidad inicial con y el ángulo cubierto por el objeto con . Las ecuaciones que gobiernan este movimiento se dan a continuación. Tenga en cuenta que estas ecuaciones son solo para situaciones en las que la aceleración angular es constante.

$\omega = \omega_o + \alpha t$

$\theta = \omega_ot + \frac{1}{2}\alpha t^2$

$\omega^2 = \omega_o^2 + 2\alpha\theta$

Ejemplos de preguntas

Pregunta 1: Si un cuerpo gira a una velocidad angular de 15 rad/s, ¿cuál sería el desplazamiento angular en 5 segundos?

Responder:

Denotemos $\omega_o$ la velocidad angular inicial.

Dado: $\omega_o = 15 \text{ rad/s}$

El objetivo es encontrar el desplazamiento angular. $\theta$

$\theta = \omega.t \\ = \theta = (15)(5) \\ = \theta = 75 \text{ rad.}$

Pregunta 2: Si un cuerpo gira con una aceleración de 2 radianes/s ² . Si la velocidad angular inicial era de 15 rad/s, ¿cuál sería la velocidad en 5 segundos?

Responder:

Denotemos $\omega_o$ la velocidad angular inicial y $\omega$ denotemos la velocidad angular final.

Dado: $\omega_o$ = 15, $\alpha$ = 2 radianes/s ²

Para averiguar el valor de «v», se puede usar la primera ecuación de movimiento.

$\omega = \omega_o + \alpha t$

Reemplazando los valores en esta ecuación,

$\omega = \omega_o + \alpha t \\ = \omega = 15 + (2)(5) \\ = \omega = 15 + (10) \\ = \omega = 25 \text{ rad/s}$

Pregunta 3: Si un cuerpo gira con una aceleración de -10 radianes/s ² . Si la velocidad angular inicial era de 30 rad/s, ¿cuál sería la velocidad en 5 segundos?

Responder:

Denotemos $\omega_o$ la velocidad angular inicial y $\omega$ denotemos la velocidad angular final.

Dado: $\omega_o = 30$ , $\alpha = -10$ radianes/s ²

Para averiguar el valor de «v», se puede usar la primera ecuación de movimiento.

$\omega = \omega_o + \alpha t$

Reemplazando los valores en esta ecuación,

$\omega = \omega_o + \alpha t \\ = \omega = 30 + (-10)(5) \\ = \omega = 30 + (-50) \\ = \omega = -20 \text{ rad/s}$

Pregunta 4: Si un cuerpo se mueve con una aceleración angular de 5 rad/s ² . Si la velocidad inicial era de 40 rad/s, ¿cuál sería el ángulo recorrido en 3 segundos?

Responder:

Sea u la velocidad inicial

Dado: $\omega_0 = 40 \text{ rad/s}$ , $\alpha = 5$ y t = 5

Para averiguar el valor de » $\theta$ «, se puede utilizar la primera ecuación de movimiento.

$\theta = \omega_ot + \frac{1}{2}\alpha t^2$

Reemplazando los valores en esta ecuación,

$\theta = \omega_ot + \frac{1}{2}\alpha t^2 \\ = \theta = (40)(3) + \frac{1}{2}(5)(3^2) \\ = \theta = 120 + \frac{1}{2}(45) \\ = \theta = 120 + 22.5 \\ = \theta = 142.5 \text{ rad}$

Pregunta 5: Si un cuerpo se mueve con una aceleración angular de 2 rad/s ² . Si la velocidad inicial era de 10 rad/s, ¿cuál sería el ángulo recorrido en 10 segundos?

Responder:

Sea u la velocidad inicial

Dado: $\omega_0 = 10 \text{ rad/s}$ , $\alpha = 2$ y t = 5

Para averiguar el valor de » $\theta$ «, se puede utilizar la primera ecuación de movimiento.

$\theta = \omega_ot + \frac{1}{2}\alpha t^2$

Reemplazando los valores en esta ecuación,

$\theta = \omega_ot + \frac{1}{2}\alpha t^2 \\ = \theta = (10)(10) + \frac{1}{2}(2)(10^2) \\ = \theta = 100 + 100 \\ = \theta = 200 \text{ rad.}$

Pregunta 6: La rueda de un coche de carreras alcanza una velocidad de 20 rad/s en 2 segundos. Encuentre el desplazamiento angular de la rueda del automóvil en el proceso.

Responder:

Denotemos $\omega_o$ la velocidad angular inicial y $\omega$ denotemos la velocidad angular final.

Dado: $\omega_o =0$ , $\omega= 20m/s$ y t= 2.

Para averiguar el valor de «a», se puede utilizar la primera ecuación de movimiento.

$\omega = \omega_o + \alpha t$

Reemplazando los valores en esta ecuación,

$\omega = \omega_o + \alpha t\\ 20 = 0 + \alpha(2) \\ 10 = \alpha$

Para averiguar la distancia, se utilizará una tercera ecuación de movimiento.

$\omega^2 = \omega_o^2 + 2\alpha\theta \\ = 20^2 = 2(\alpha)(\theta) \\ = 400 = 2(10)(\theta) \\ = 20 = \theta$

Pregunta 7: La rueda de un coche de carreras alcanza una velocidad de 40 rad/s en 4 segundos. Encuentre el desplazamiento angular de la rueda del automóvil en el proceso.

Responder:

Denotemos $\omega_o$ la velocidad angular inicial y $\omega$ denotemos la velocidad angular final.

Dado: $\omega_o =0$ , $\omega= 40\text{ rad/s}$ y t = 4.

Para averiguar el valor de «a», se puede utilizar la primera ecuación de movimiento.

$\omega = \omega_o + \alpha t$

Reemplazando los valores en esta ecuación,

$\omega = \omega_o + \alpha t\\ 40 = 0 + \alpha(4) \\ 10 = \alpha$

Para averiguar la distancia, se utilizará una tercera ecuación de movimiento.

$\omega^2 = \omega_o^2 + 2\alpha\theta \\ = 40^2 = 2(\alpha)(\theta) \\ = 1600 = 2(10)(\theta) \\ = 80 = \theta$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA