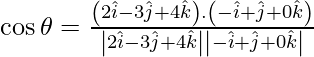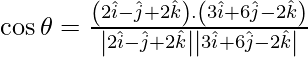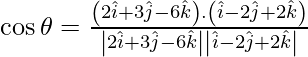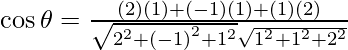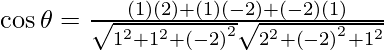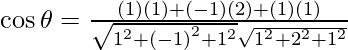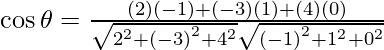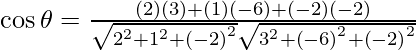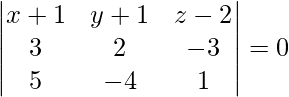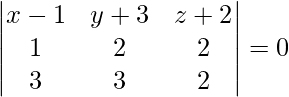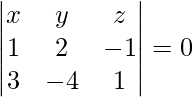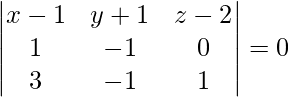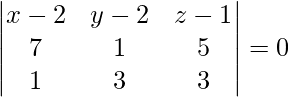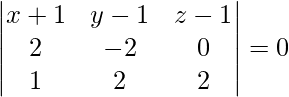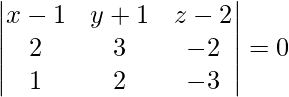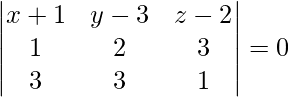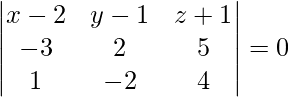Pregunta 1. Encuentra el ángulo entre los planos dados:
(yo) 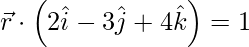 y
y 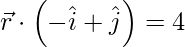
Solución:
Dado
y
Como sabemos que el ángulo entre los planos
está dado por,
Aquí,
Asi que,
=
=
=
Por lo tanto,
.
(ii) 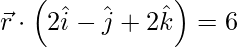 y
y 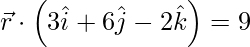
Solución:
Dado
y
Como sabemos que el ángulo entre los planos
está dado por,
Aquí,
Asi que,
=
=
= -4/21
Por lo tanto, θ = cos -1 (-4/21).
(iii) 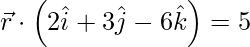 y
y 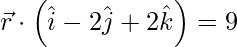
Solución:
Dado
y
Como sabemos que el ángulo entre los planos,
viene dado por,
Aquí,
Asi que,
=
=
= -16/21
Por lo tanto, θ = cos -1 (-16/21).
Pregunta 2. Encuentra el ángulo entre los planos:
(i) 2x − y + z = 4 y x + y + 2z = 3
Solución:
Dado, 2x − y + z = 4 y x + y + 2z = 3
Como sabemos que el ángulo entre los planos a 1 x + b 1 y + c 1 z + d 1 = 0 y a 2 x + b 2 y + c 2 z + d 2 = 0 está dado por,
Entonces, el ángulo entre 2x – y + z = 4 y x + y + 2z = 3 está dado por,
=
=
= 3/6
= 1/2
Por tanto, θ = cos -1 (1/2) = π/3.
(ii) x + y − 2z = 3 y 2x − 2y + z = 5
Solución:
Dado, x + y − 2z = 3 y 2x − 2y + z = 5
Como sabemos que el ángulo entre los planos a 1 x + b 1 y + c 1 z + d 1 = 0 y a 2 x + b 2 y + c 2 z + d 2 = 0 está dado por,
Entonces, el ángulo entre x + y – 2z = 3 y 2x – 2y + z = 5 está dado por,
=
=
= -2/3√6
Por lo tanto, θ = cos -1 (-2/3√6).
(iii) x − y + z = 5 y x + 2y + z = 9
Solución:
Dado, x − y + z = 5 y x + 2y + z = 9
Como sabemos que el ángulo entre los planos a 1 x + b 1 y + c 1 z + d 1 = 0 y a 2 x + b 2 y + c 2 z + d 2 = 0 está dado por,
Entonces, el ángulo entre x – y + z = 5 y x + 2y + z = 9 está dado por,
=
=
= 0
Por lo tanto, θ = cos -1 (0) = π/2.
(iv) 2x − 3y + 4z = 1 y − x + y = 4
Solución:
Dado, 2x − 3y + 4z = 1 y − x + y = 4
Como sabemos que el ángulo entre los planos a 1 x + b 1 y + c 1 z + d 1 = 0 y a 2 x + b 2 y + c 2 z + d 2 = 0 está dado por,
Entonces, el ángulo entre 2x – 3y + 4z = 1 y -x + y + 0z = 4 está dado por,
=
=
=
Por lo tanto,
.
(v) 2x + y − 2z = 5 y 3x − 6y − 2z = 7
Solución:
Dado, 2x + y − 2z = 5 y 3x − 6y − 2z = 7
Como sabemos que el ángulo entre los planos a 1 x + b 1 y + c 1 z + d 1 = 0 y a 2 x + b 2 y + c 2 z + d 2 = 0 está dado por,
Entonces, el ángulo entre 2x + y – 2z = 5 y 3x – 6y – 2z = 7 está dado por,
=
=
= 4/21
Por lo tanto, θ = cos -1 (4/21).
Pregunta 3. Demuestra que los siguientes planos forman ángulos rectos.
(yo) 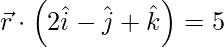 y
y 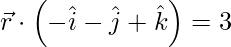
Solución:
dado,
y
Como sabemos que los planos
son perpendiculares entre sí solo si
.
Aquí,
Ahora tenemos
= -2 + 1 + 1
= 0
Entonces, los planos dados son perpendiculares.
Por lo tanto probado.
(ii) x − 2y + 4z = 10 y 18x + 17y + 4z = 49
Solución:
Dado, x − 2y + 4z = 10 y 18x + 17y + 4z = 49
Como sabemos que los planos a 1 x + b 1 y + c 1 z + d 1 = 0 y a 2 x + b 2 y + c 2 z + d 2 = 0 son perpendiculares entre sí solo si,
=> un 1 un 2 + segundo 1 segundo 2 + do 1 do 2 = 0
Los planos dados son x – 2y + 4z = 10 y 18x + 17y + 4z = 49.
Aquí, a 1 = 1, b 1 = – 2, c 1 = 4, a 2 = 18, b 2 = 17 y c 2 = 4
Ahora tenemos
un 1 un 2 + segundo 1 segundo 2 + c 1 c 2 = ( 1) (18) + (- 2) (17) + (4) (4)
= 18 – 34 + 16
= 0
Entonces, los planos dados son perpendiculares.
Por lo tanto probado.
Pregunta 4. Determina el valor de λ para el cual los siguientes planos son perpendiculares entre sí.
(yo) 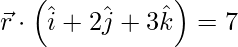 y
y 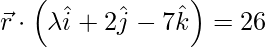
Solución:
dado,
y
Como sabemos que los planos,
son perpendiculares entre sí solo si,
.
Aquí,
Los planos dados son perpendiculares. Entonces tenemos
λ + 4 – 21 = 0
λ – 17 = 0
l = 17
Por lo tanto, el valor de λ es 17.
(ii) 2x − 4y + 3z = 5 y x + 2y + λz = 5
Solución:
Dado, 2x − 4y + 3z = 5 y x + 2y + λz = 5
Como sabemos que los planos a 1 x + b 1 y + c 1 z + d 1 = 0 y a 2 x + b 2 y + c 2 z + d 2 = 0 son perpendiculares entre sí solo si,
=> un 1 un 2 + segundo 1 segundo 2 + do 1 do 2 = 0
Los planos dados son 2x – 4y + 3z = 5 y x + 2y + λz = 5.
Aquí, a 1 = 2, b 1 = – 4, c 1 = 3, a 2 = 1, b 2 = 2 y c 2 = λ.
Se da que los planos dados son perpendiculares. Entonces, obtenemos
un 1 un 2 + segundo 1 segundo 2 + do 1 do 2 = 0
(2) (1) + (-4) (2) + (3) (λ) = 0
2 – 8 + 3λ = 0
3λ = 6
λ = 2
Por lo tanto, el valor de λ es 2.
(iii) 3x − 6y − 2z = 7 y 2x + y − λz = 5
Solución:
Dado, 3x − 6y − 2z = 7 y 2x + y − λz = 5
Como sabemos que los planos a 1 x + b 1 y + c 1 z + d 1 = 0 y a 2 x + b 2 y + c 2 z + d 2 = 0 son perpendiculares entre sí solo si,
=> un 1 un 2 + segundo 1 segundo 2 + do 1 do 2 = 0
Los planos dados son 3x – 6y – 2z = 7 y 2x + y – λz = 5.
Aquí, a 1 = 3, b 1 = – 6, c 1 = – 2, a 2 = 2, b 2 = 1 y c 2 = -λ
Aquí, los planos dados son perpendiculares.
un 1 un 2 + segundo 1 segundo 2 + do 1 do 2 = 0
(3) (2) + (-6) (1) + (-2) (λ) = 0
6 – 6 + 2λ = 0
2λ = 0
λ = 0
Pregunta 5. Encuentra la ecuación de un plano que pasa por el punto (−1, −1, 2) y es perpendicular a los planos 3x + 2y − 3z = 1 y 5x − 4y + z = 5.
Solución:
La ecuación de cualquier plano que pasa por (-1, -1, 2) es,
una (x + 1) + segundo (y + 1) + c (z – 2) = 0 . . . . (1)
Se da que la ecuación anterior es perpendicular a cada uno de los planos 3x + 2y – 3z = 1 y 5x – 4y + z = 5.
3a + 2b – 3c = 0 . . . . (2)
5a – 4b + c = 0 . . . . (3)
Al resolver las ecuaciones (1), (2) y (3), obtenemos,
-10 (x + 1) – 18 (y + 1) – 22 (z – 2) = 0
-5 (x + 1) – 9 (y + 1) – 11 (z – 2) = 0
5x + 5 + 9y + 9 + 11z – 22 = 0
5x + 9y + 11z – 8 = 0
Por lo tanto, la ecuación del plano es 5x + 9y + 11z – 8 = 0
Pregunta 6. Obtenga la ecuación del plano que pasa por el punto (1, −3, −2) y es perpendicular a los planos x + 2y + 2z = 5 y 3x + 3y + 2z = 8.
Solución:
La ecuación de cualquier plano que pasa por (1, -3, -2) es,
una (x – 1) + segundo (y + 3) + c (z + 2) = 0 . . . . (1)
Se da que la ecuación anterior es perpendicular a los planos x + 2y + 2z = 5 y 3x + 3y + 2z = 8.
un + 2b + 2c = 0 . . . . (2)
3a + 3b + 2c = 0 . . . . (3)
Al resolver las ecuaciones (1), (2) y (3), obtenemos,
-2 (x – 1) + 4 (y + 3) – 3 (z + 2) = 0
-2x + 2 + 4y + 12 – 3z – 6 = 0
2x – 4y + 3z – 8 = 0
Por lo tanto, la ecuación del plano es 2x – 4y + 3z – 8 = 0
Pregunta 7. Encuentra la ecuación del plano que pasa por el origen y es perpendicular a cada uno de los planos x + 2y − z = 1 y 3x − 4y + z = 5.
Solución:
La ecuación de cualquier plano que pasa por el origen (0, 0, 0) es,
un (x – 0) + segundo (y – 0) + c (z – 0) = 0 . . . . (1)
hacha + por + cz = 0
Se da que la ecuación anterior es perpendicular a los planos x + 2y – z = 1 y 3x – 4y + z = 5.
un + 2b – c = 0 . . . . (2)
3a – 4b + c = 0 . . . . (3)
Al resolver la ecuación (1), (2) y (3), obtenemos,
– 2x – 4y – 10z = 0
x + 2y + 5z = 0
Por lo tanto, la ecuación del plano es x + 2y + 5z = 0
Pregunta 8. Encuentra la ecuación del plano que pasa por los puntos (1, −1, 2) y (2, −2, 2) y que es perpendicular al plano 6x − 2y + 2z = 9.
Solución:
La ecuación de cualquier plano que pasa por (1, -1, 2) es,
una (x – 1) + segundo (y + 1) + c (z – 2) = 0 . . . . (1)
Se da que la ecuación anterior está pasando por (2, -2, 2). Asi que,
a (2 – 1) + b (-2 + 1) + c (2 – 2) = 0
un – segundo = 0 . . . . (2)
Se da que la ecuación anterior es perpendicular al plano 6x – 2y + 2z = 9. Entonces,
6a – 2b + 2c = 0
3a – segundo + c = 0 . . . . (3)
Al resolver la ecuación (1), (2) y (3), obtenemos,
-1 (x – 1) – 1 (y + 1) + 2 (z – 2) = 0
– x + 1 – y – 1 + 2z – 4 = 0
x + y – 2z + 4 = 0
Por lo tanto, la ecuación del plano es x + y – 2z + 4 = 0
Pregunta 9. Encuentra la ecuación del plano que pasa por los puntos (2, 2, 1) y (9, 3, 6) y es perpendicular al plano 2x + 6y + 6z = 1.
Solución:
La ecuación de cualquier plano que pasa por (2, 2, 1) es,
una (x – 2) + segundo (y – 2) + c (z – 1) = 0 . . . . (1)
Se da que la ecuación anterior pasa por (9, 3, 6). Asi que,
a (9 – 2) + b (3 – 2) + c (6 – 1) = 0
7a + segundo + 5c = 0 . . . . (2)
Se da que la ecuación anterior es perpendicular al plano 2x + 6y + 6z = 1. Entonces,
2a + 6b + 6c = 0
a + 3b + 3c = 0 . . . . (3)
Al resolver las ecuaciones (1), (2) y (3), obtenemos
-12 (x – 2) – 16 (y – 2) + 20 (z – 1) = 0
3 (x – 2) + 4 (y – 2) – 5 (z – 1) = 0
3x + 4y – 5z = 9
Por lo tanto, la ecuación del plano es 3x + 4y – 5z = 9
Pregunta 10. Encuentra la ecuación del plano que pasa por los puntos cuyas coordenadas son (−1, 1, 1) y (1, −1, 1) y perpendicular al plano x + 2y + 2z = 5.
Solución:
La ecuación de cualquier plano que pasa por (-1, 1, 1) es,
una (x + 1) + segundo (y – 1) + c (z – 1) = 0 . . . . (1)
Se da que la ecuación anterior pasó por (1, -1, 1). Asi que,
a (1 + 1) + b (-1 – 1) + c (1 – 1) = 0
2a – 2b = 0 . . . . (2)
Se da que la ecuación anterior es perpendicular al plano x + 2y + 2z = 5. Entonces,
un + 2b + 2c = 0 . . . . (3)
Al resolver las ecuaciones (1), (2) y (3), obtenemos
-4 (x + 1) – 4 (y – 1) + 6 (z – 1) = 0
2 (x + 1) + 2 (y – 1) – 3 (z – 1) = 0
2x + 2y – 3z + 3 = 0
Por lo tanto, la ecuación del plano es 2x + 2y – 3z + 3 = 0
Pregunta 11. Encuentra la ecuación del plano con intersección 3 en el eje y y paralelo al plano ZOX.
Solución:
La ecuación del plano paralelo al plano ZOX es,
y = segundo . . . . (1)
Según la pregunta, se da que este plano pasa por (0, 3, 0). Asi que,
=> segundo = 3
Al sustituir este valor en la ecuación (1), obtenemos
y = 3,
Por lo tanto, la ecuación del plano es
y = 3
Pregunta 12. Encuentra la ecuación del plano que contiene el punto (1, −1, 2) y es perpendicular a cada uno de los planos 2x + 3y − 2z = 5 y x + 2y − 3z = 8.
Solución:
La ecuación de cualquier plano que pasa por (1, -1, 2) es,
una (x – 1) + segundo (y + 1) + c (z – 2) = 0 . . . . (1)
Se da que la ecuación anterior es perpendicular al plano 2x + 3y – 2z = 5. Entonces,
2a + 3b – 2c = 0 . . . . (2)
Se da que la ecuación anterior es perpendicular al plano x + 2y – 3z = 8. Entonces,
a + 2b – 3c = 0 . . . . (3)
Entonces, al resolver las ecuaciones (1), (2) y (3), obtenemos
-5 (x – 1) + 4 (y + 1) + 1 (z – 2) = 0
5x – 4y – z = 7
Por lo tanto, la ecuación del plano es 5x – 4y – z = 7
Pregunta 13. Encuentra la ecuación del plano que pasa por (a, b, c) y paralelo al plano 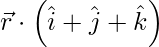 = 2.
= 2.
Solución:
La ecuación dada del plano es \vec{r} \cdot \left( \hat{i} + \hat{j} + \hat{k} \right) = 2
Entonces, al sustituir
en la ecuación dada del plano, obtenemos
=> x + y + z – 2 = 0 . . . . (1)
La ecuación de un plano que es paralelo al plano (ecuación 1) es de la forma,
x + y + z = k . . . . (2)
Se da que la ecuación anterior del plano pasa por el punto (a, b, c). Asi que,
un + segundo + c = k
Al sustituir este valor de k en la ecuación (2), obtenemos
x + y + z = a + b + c
Por lo tanto, la ecuación del plano es
x + y + z = a + b + c
Pregunta 14. Encuentra la ecuación del plano que pasa por el punto (−1, 3, 2) y es perpendicular a cada uno de los planos x + 2y + 3z = 5 y 3x + 3y + z = 0.
Solución:
La ecuación de cualquier plano que pasa por el punto (-1, 3, 2) es,
una (x + 1) + segundo (y – 3) + c (z – 2) = 0 . . . . (1)
Se da que la ecuación anterior es perpendicular al plano x + 2y + 3z = 5. Entonces,
un + 2b + 3c = 0 . . . . (2)
Se da que la ecuación anterior es perpendicular al plano 3x + 3y + z = 0. Entonces,
3a + 3b + c = 0 . . . . (3)
Al resolver las ecuaciones (1), (2) y (3), obtenemos
-7 (x + 1) + 8 (y – 3) – 3 (z – 2) = 0
7x – 8y + 3z + 25 = 0
Por lo tanto, la ecuación del plano es
7x – 8y + 3z + 25 = 0
Pregunta 15. Encuentra la ecuación vectorial del plano que pasa por los puntos (2, 1, −1) y (−1, 3, 4) y es perpendicular al plano x − 2y + 4z = 10.
Solución:
La ecuación de cualquier plano que pasa por (2, 1, -1) es,
una (x – 2) + segundo (y – 1) + c (z + 1) = 0 . . . . (1)
Se da que la ecuación anterior pasa por (-1, 3, 4). Asi que,
a (-1 – 2) + b (3 – 1) + c (4 + 1) = 0
-3a + 2b + 5c . . . . (2)
Se da que la ecuación anterior es perpendicular al plano x – 2y + 4z = 10. Entonces,
a – 2b + 4c = 0 . . . . (3)
Al resolver las ecuaciones (1), (2) y (3), obtenemos
18 (x – 2) + 17 (y – 1) + 4 (z + 1) = 0
18x + 17y + 4z – 49 = 0
Por lo tanto, la ecuación del plano es
18x + 17y + 4z – 49 = 0
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA