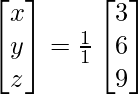
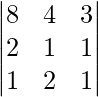
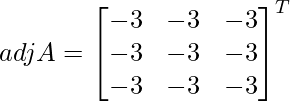
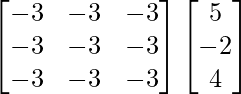
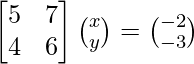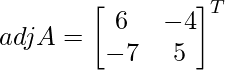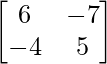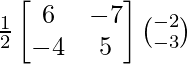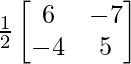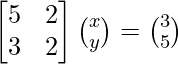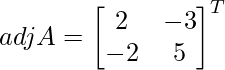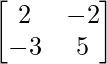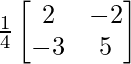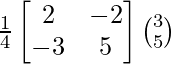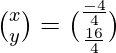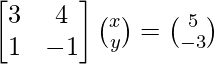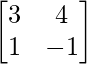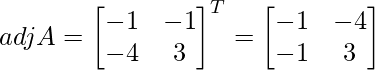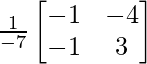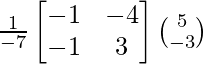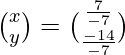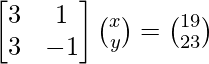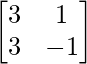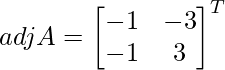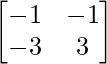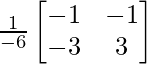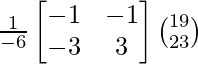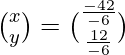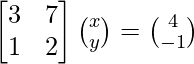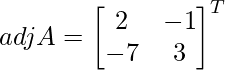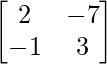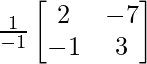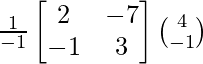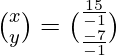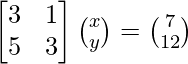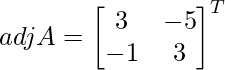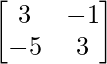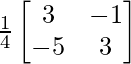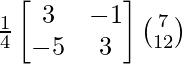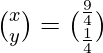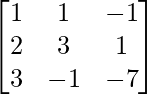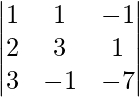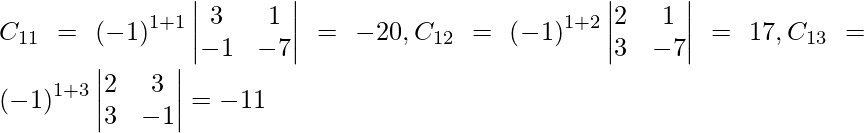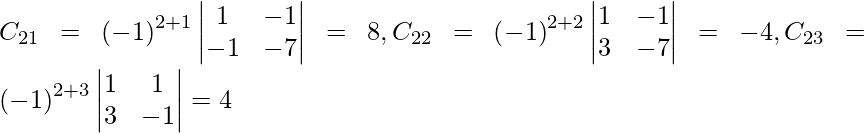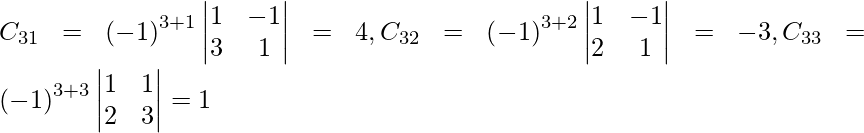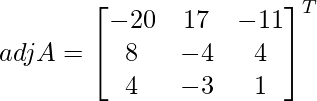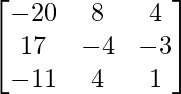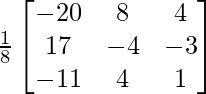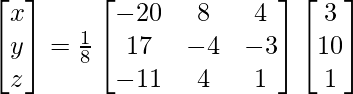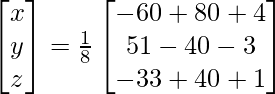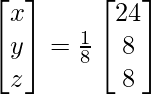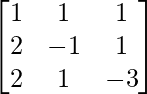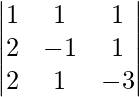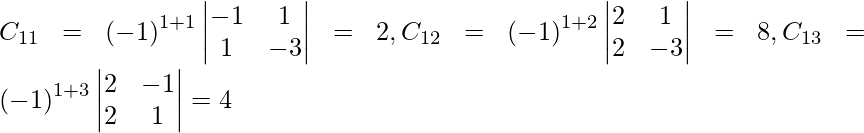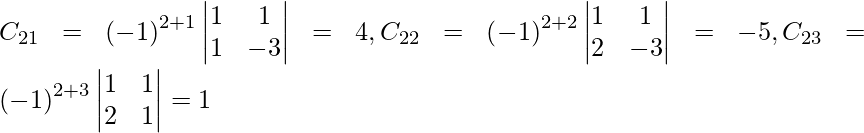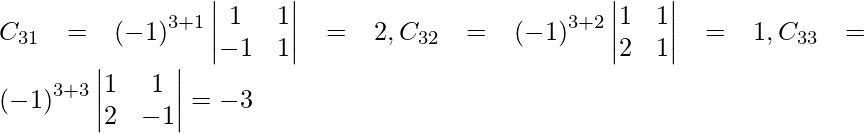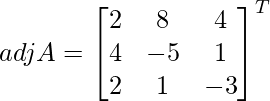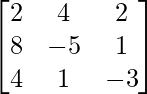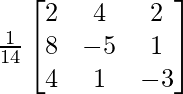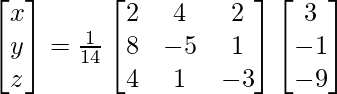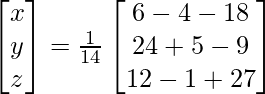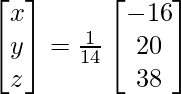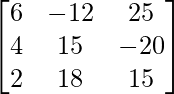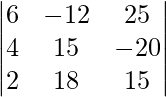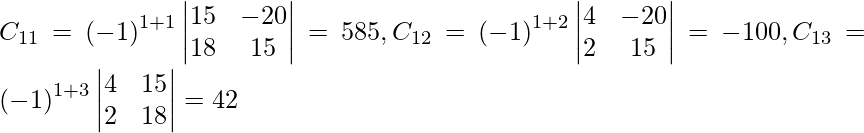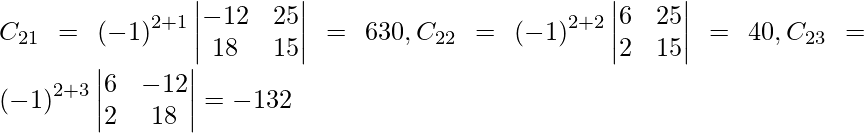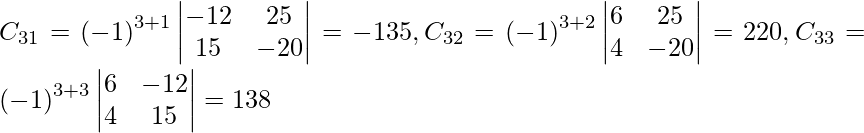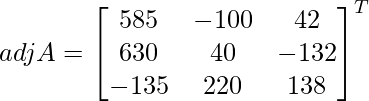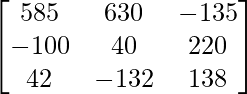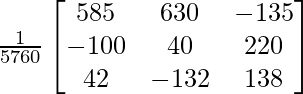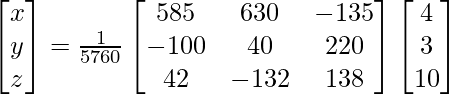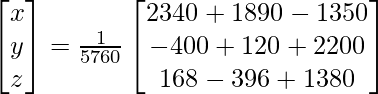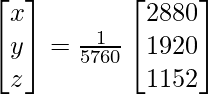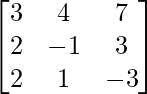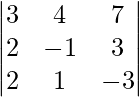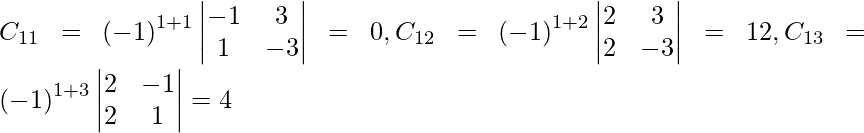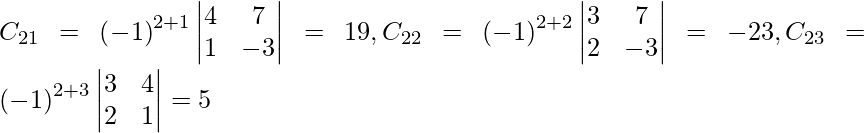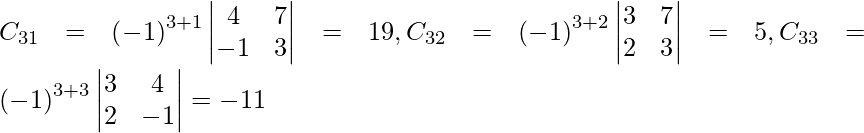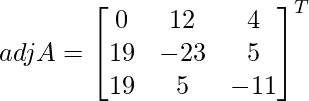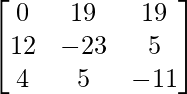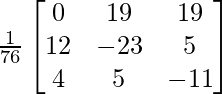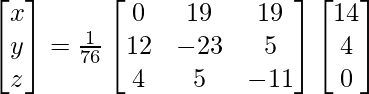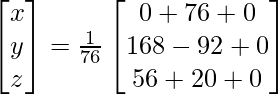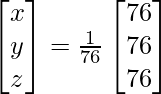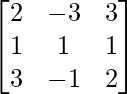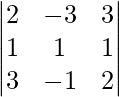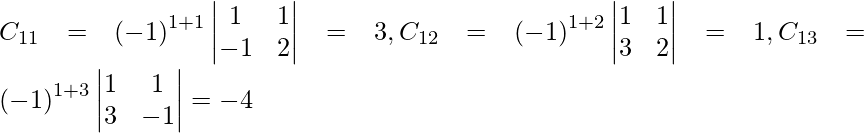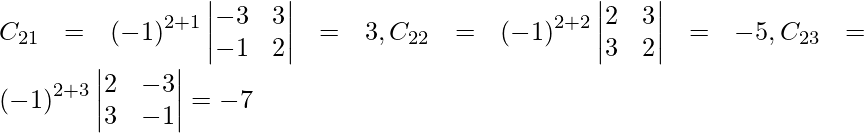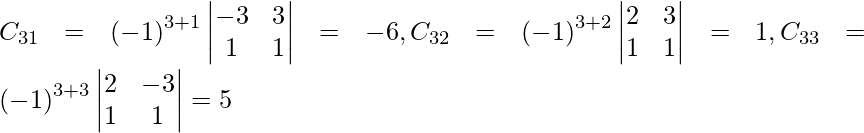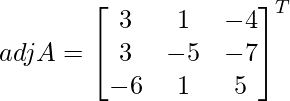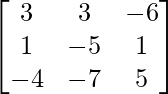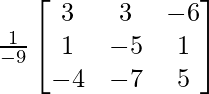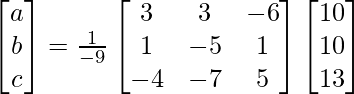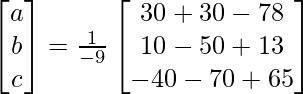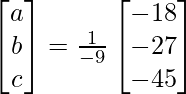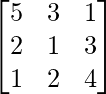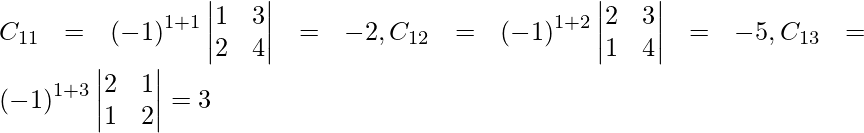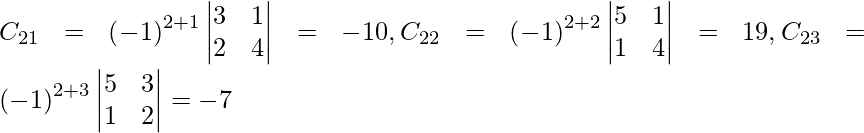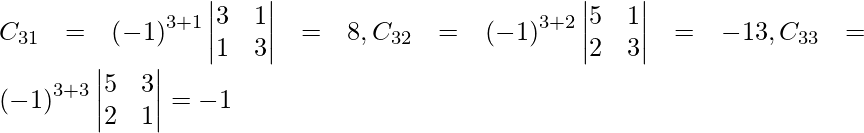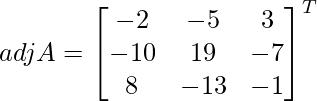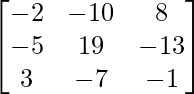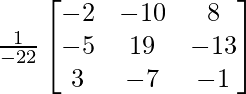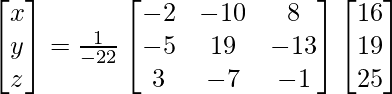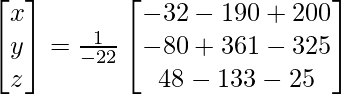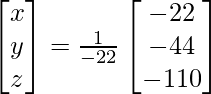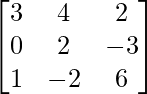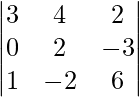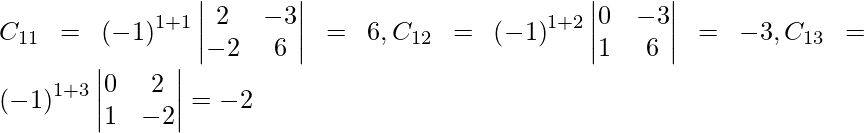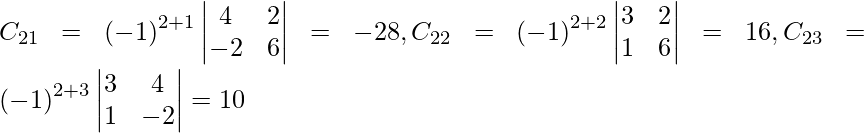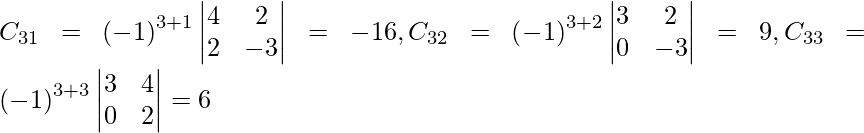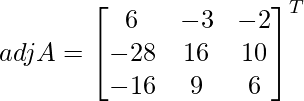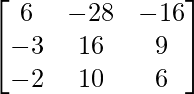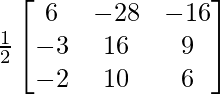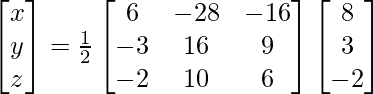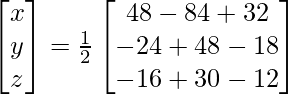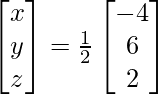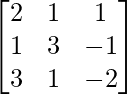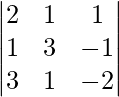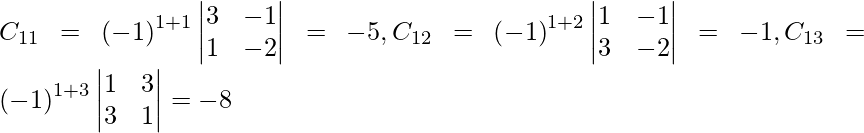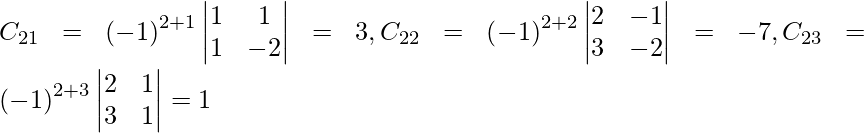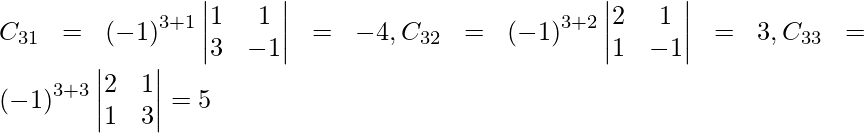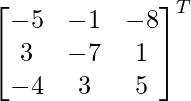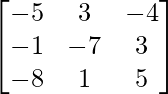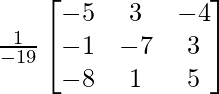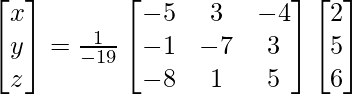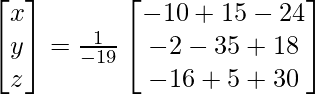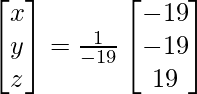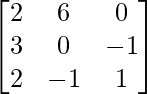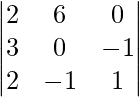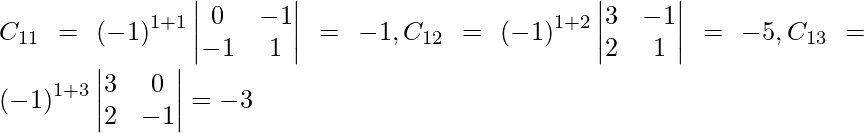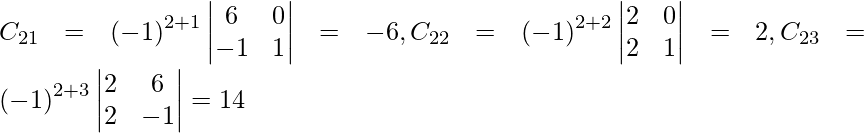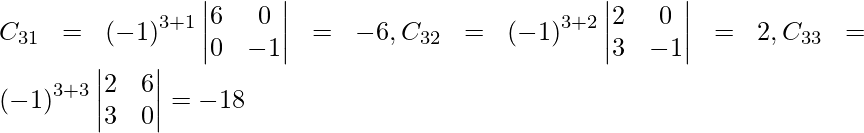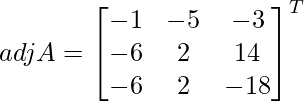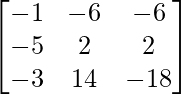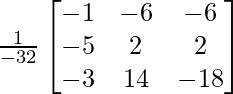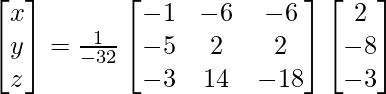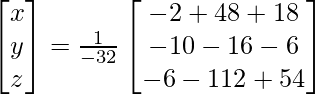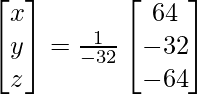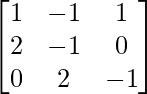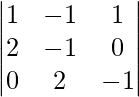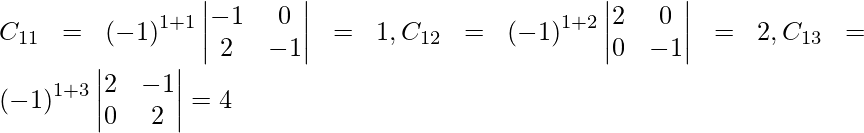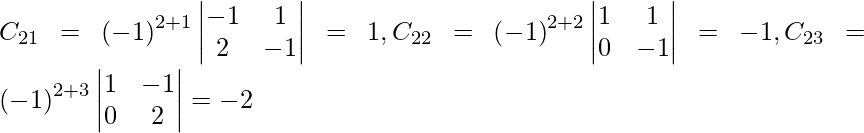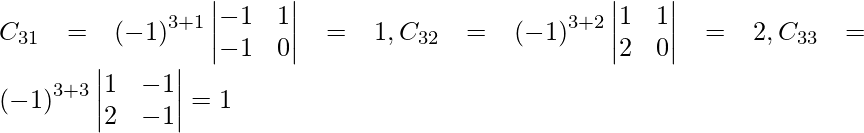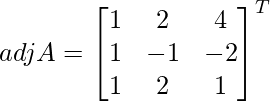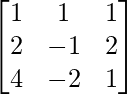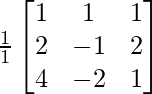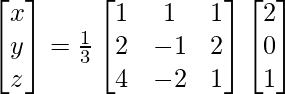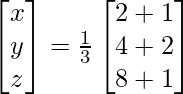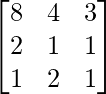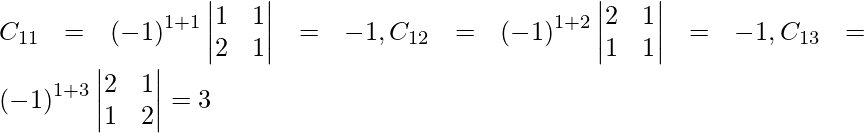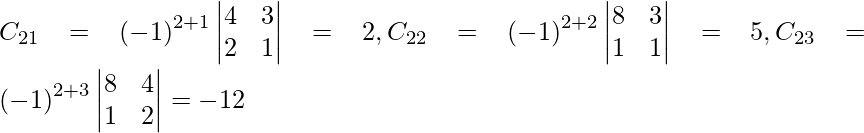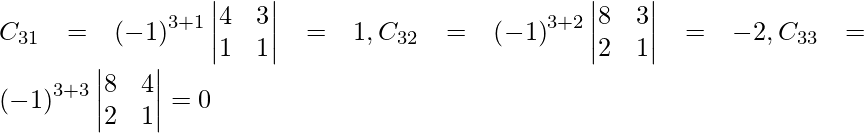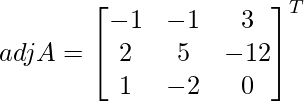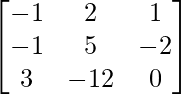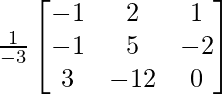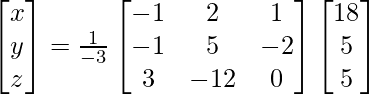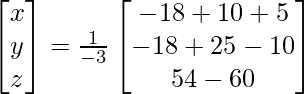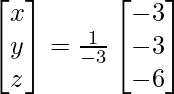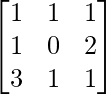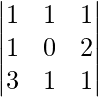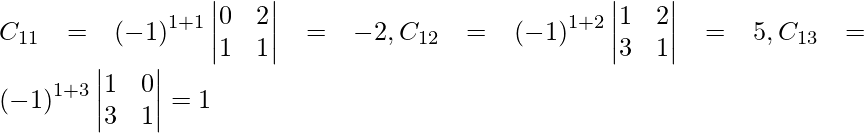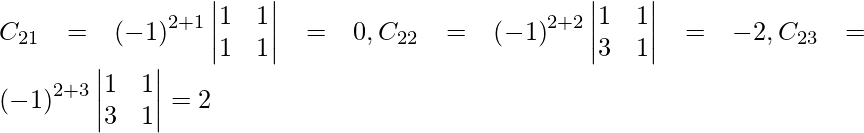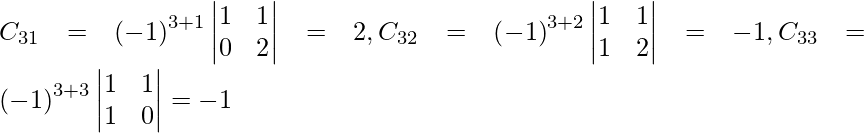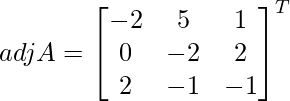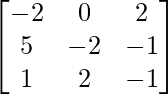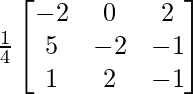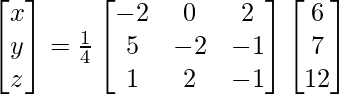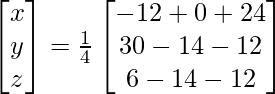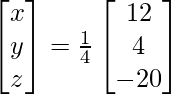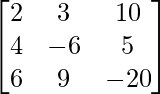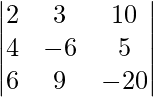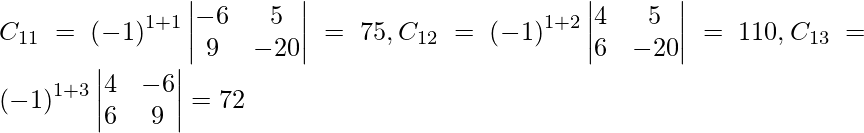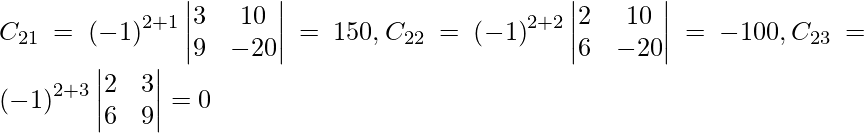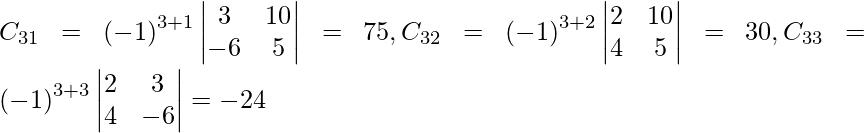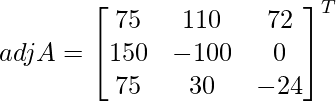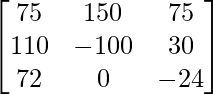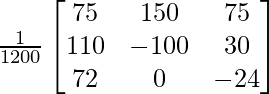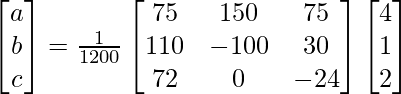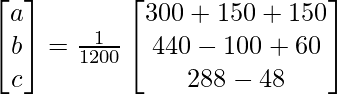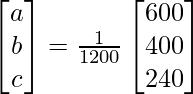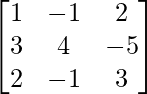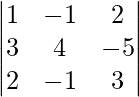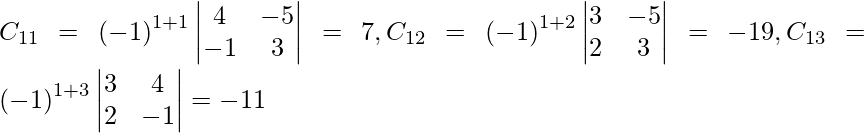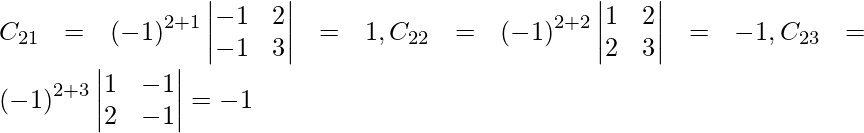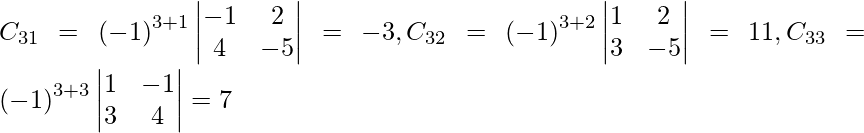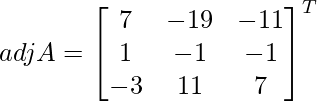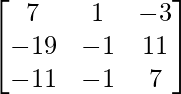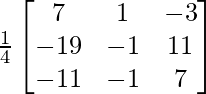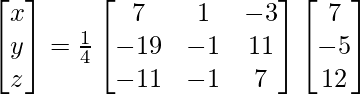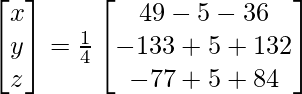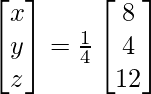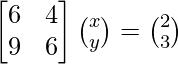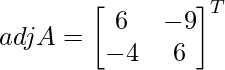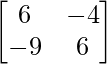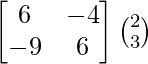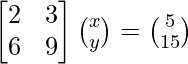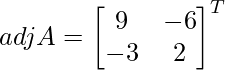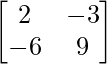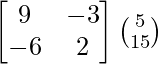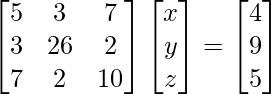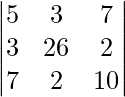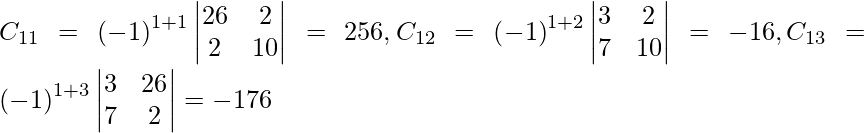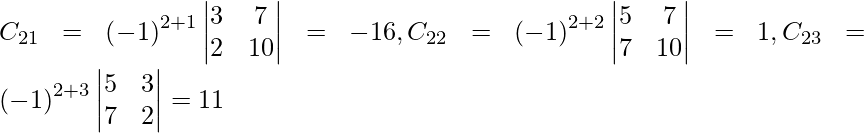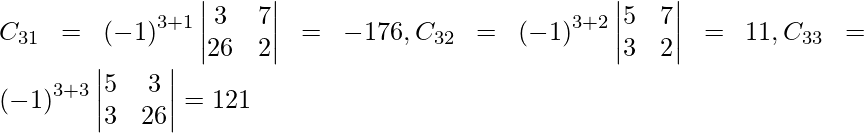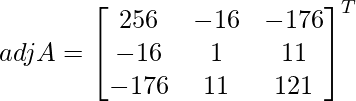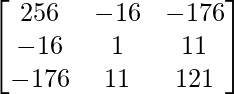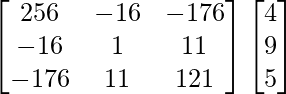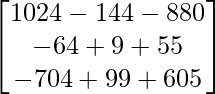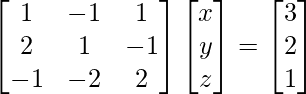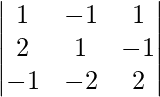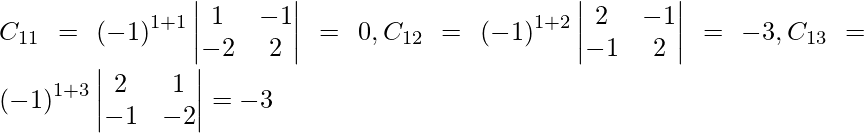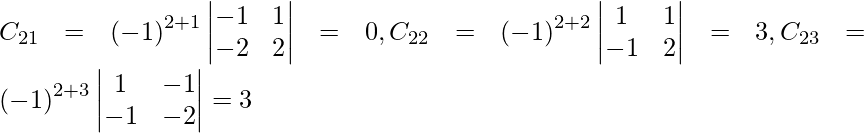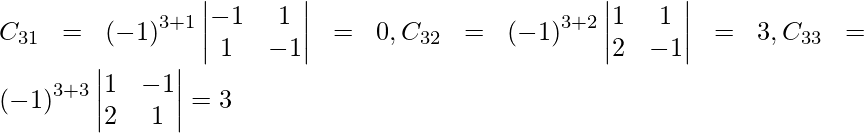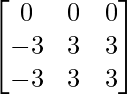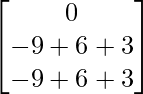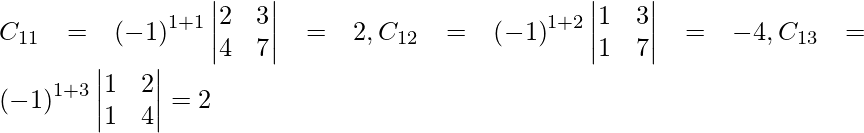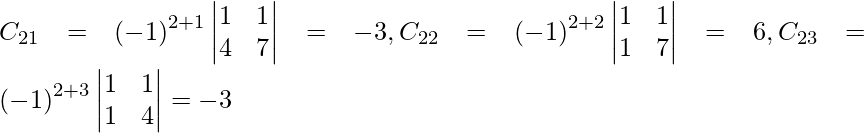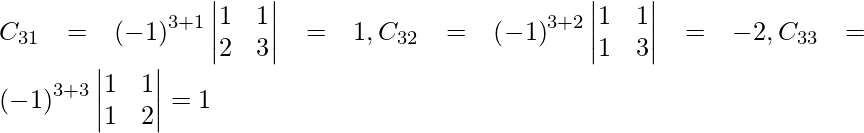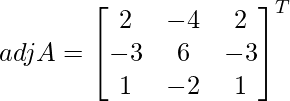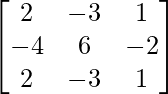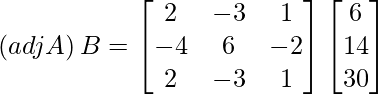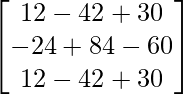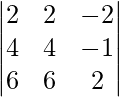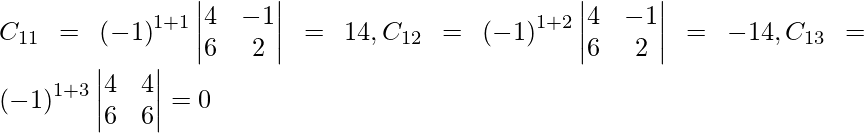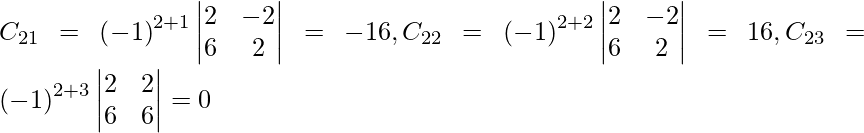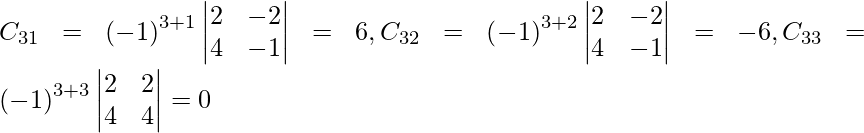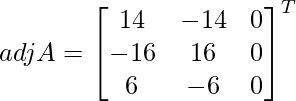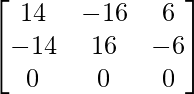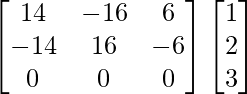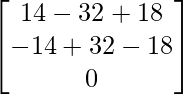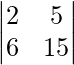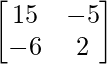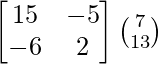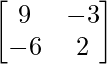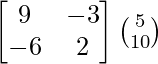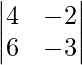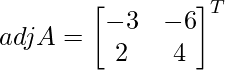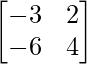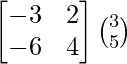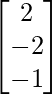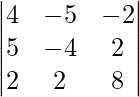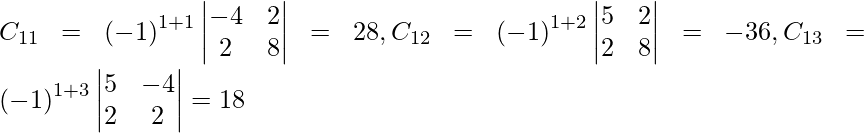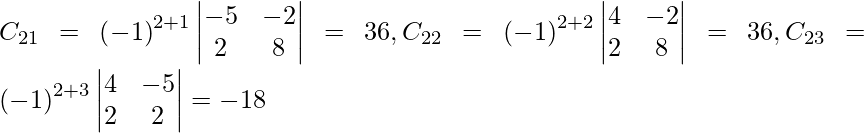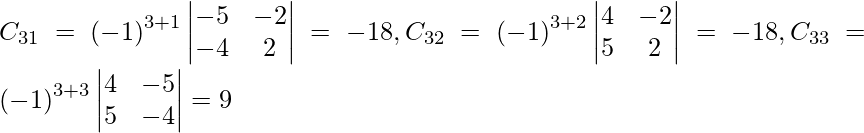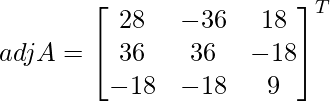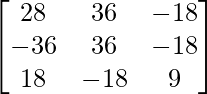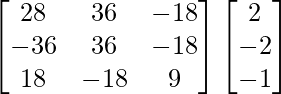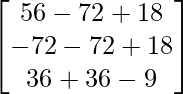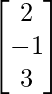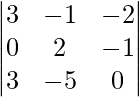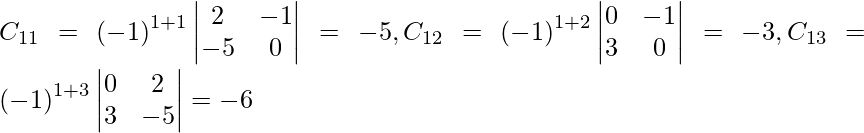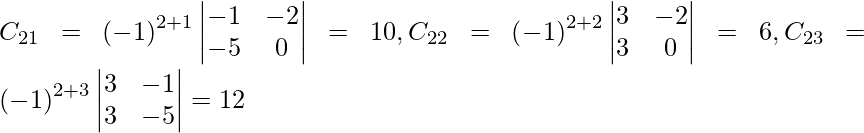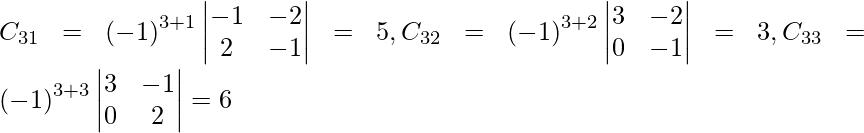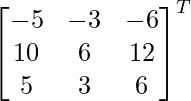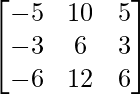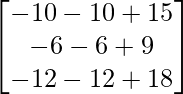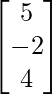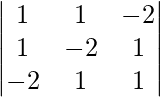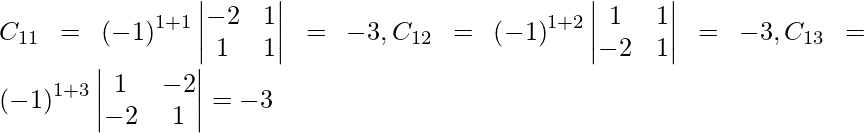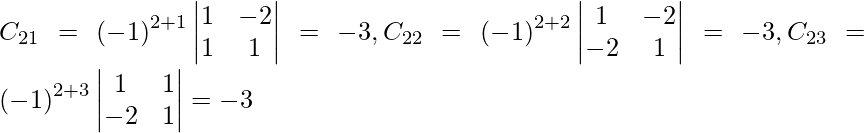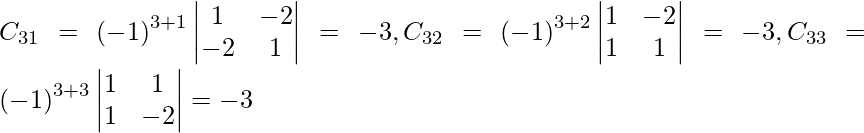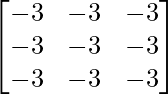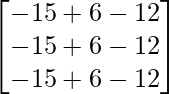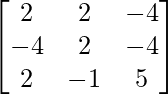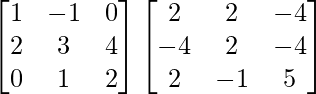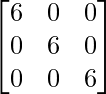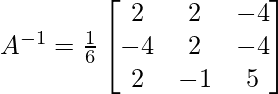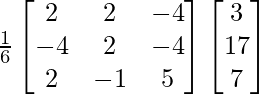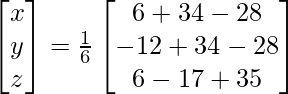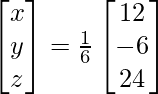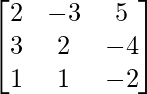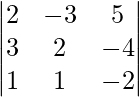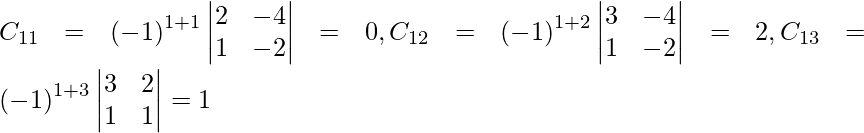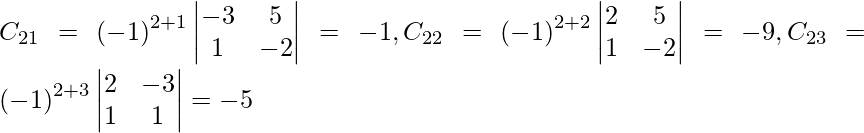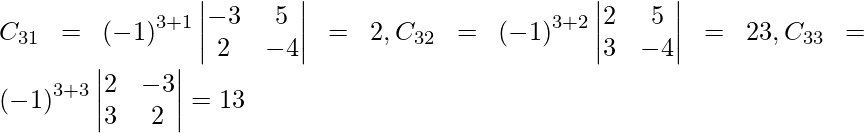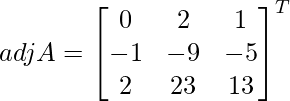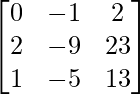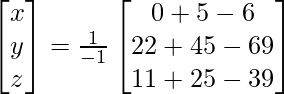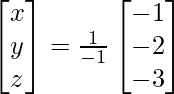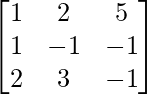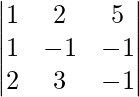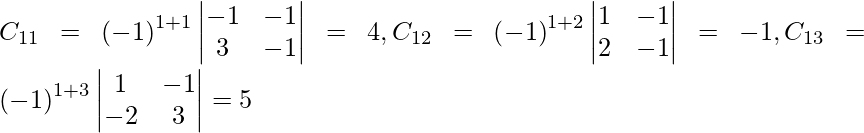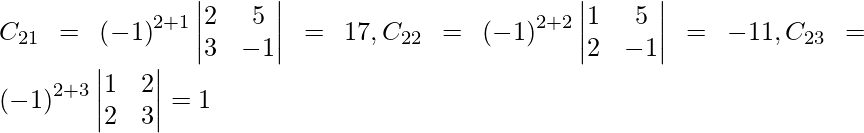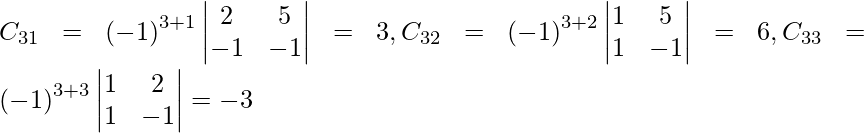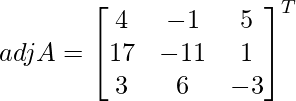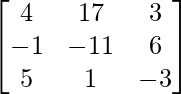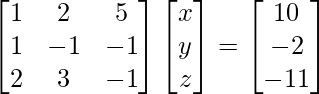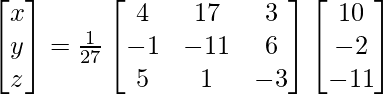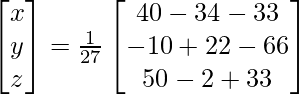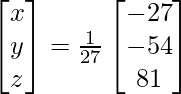Pregunta 1. Resuelve el siguiente sistema de ecuaciones por el método matricial:
(yo) 5x + 7y + 2 = 0
4x + 6y + 3 = 0
Solución:
El sistema de ecuaciones dado se puede escribir en forma matricial como,
AX = B
Aquí,
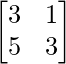
A =
, X =
y B =
Ahora,
|A| =
= 30 – 28
= 2
El sistema dado tiene una solución única dada por, X = A -1 B.
Sea C ij el cofactor de los elementos a ij en A.
C 11 = (-1) 1+1 (6) = 6, C 12 = (-1) 1+2 (4) = -4, C 21 = -1 2+1 (7) = -7 y C 22 = (-1) 2+2 (5) = 5
=
A – 1 =
A – 1 =
Entonces, X = A -1 B
=
=
=>
Por tanto, x = 9/2 ey = -7/2.
(ii) 5x + 2y = 3
3x + 2y = 5
Solución:
El sistema de ecuaciones dado se puede escribir en forma matricial como,
AX = B
Aquí,
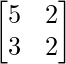
A =
, X =
y B =
Ahora,
|A| =
= 10 – 6
= 4
El sistema dado tiene una solución única dada por, X = A -1 B
Sea C ij el cofactor de los elementos a ij en A.
C 11 = -1 1+1 (2) = 2, C 12 = (-1) 1+2 (3) = – 3, C 21 = (-1) 2+1 (2) = – 2 y C 22 = (-1) 2+2 (5) = 5
=
A – 1 =
=
Ahora, X = A -1 B
=
=
=>
Por lo tanto, x = – 1 y y = 4.
(iii) 3x + 4y − 5 = 0
x – y + 3 = 0
Solución:
El sistema de ecuaciones dado se puede escribir en forma matricial como,
AX = B
Aquí,
A =
, X =
y B =
Ahora,
|A| =
= – 3 – 4
= -7
Entonces, el sistema dado tiene una solución única dada por, X = A -1 B
Sean C ij los cofactores de los elementos a ij en A.
C 11 = (-1) 1+1 (1) = -1, C 12 = (-1) 1+2 (-1) = 1, C 21 = (-1) 2+1 (4) = -4 y C 22 = (-1) 2+2 (3) = 3
=
Ahora, X = A -1 B
=
=
=>
Por lo tanto, x = -1 y y = 2.
(iv) 3x + y = 19
3x − y = 23
Solución:
El sistema de ecuaciones dado se puede escribir en forma matricial como,
AX = B
Aquí,
A =
, X =
y B =
Ahora,
|A| =
= – 3 – 3
= -6
Entonces, el sistema dado tiene una solución única dada por X = A -1 B.
Sean C ij los cofactores de los elementos a ij en A.
C 11 = (-1) 1+1 (-1) = -1, C 12 = (-1) 1+2 (3) = -3, C 21 = (-1) 2+1 (1) = – 4 y C 22 = (-1) 2+2 (3) = 3
=
=
Ahora, X = A -1 B
=
=
=>
Por lo tanto, x = 7 yy = -2.
(v) 3x + 7y = 4
x + 2y = −1
Solución:
El sistema de ecuaciones dado se puede escribir en forma matricial como,
AX = B
Aquí,
A =
, X =
y B =
Ahora,
|A| =
= 6 – 7
= -1
Entonces, el sistema dado tiene una solución única dada por X = A -1 B.
Sean C ij los cofactores de los elementos a ij en A.
C 11 = (-1) 1+1 (2) = 2, C 12 = (-1) 1+2 (1) = -1, C 21 = (-1) 2+1 (7) = -7 y C22 = (-1) 2 +2 (3) = 3
=
=
X = A -1B
=
=
=>
Por lo tanto x = – 15 y y = 7.
(vi) 3x + y = 7
5x + 3y = 12
Solución:
El sistema de ecuaciones dado se puede escribir en forma matricial como,
AX = B
Aquí,
A =
, X =
y B =
Ahora,
|A| =
= 9 – 5
= 4
Entonces, el sistema dado tiene una solución única dada por X = A -1 B.
Sean C ij los cofactores de los elementos a ij en A.
C 11 = (-1) 1+1 (3) = 3, C 12 = (-1) 1+2 (5) = -5, C 21 = (-1) 2+1 (1) = -1 y C22 = (-1) 2 +2 (3) = 3
=
=
X = A -1B
=
=
=>
Por lo tanto x = 9/4 ey = 1/4.
Pregunta 2. Resuelve el siguiente sistema de ecuaciones por el método matricial:
(yo) x + y − z = 3
2x + 3y + z = 10
3x – y – 7z = 1
Solución:
un =
|A| =
= 1 (-21 + 1) – 1(-14 – 3) – 1(-2 – 9)
= – 20 + 17 + 11
= 8
Entonces, el sistema dado tiene una solución única dada por X = A -1 B.
Sea C ij el cofactor de los elementos a ij en A.
=
=
X = A -1B
=> x = 24/8, y = 8/8 y z = 8/8
Por lo tanto, x = 3, y = 1 y z = 1.
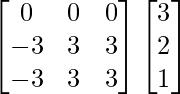
(ii) x + y + z = 3
2x – y + z = – 1
2x + y − 3z = − 9
Solución:
un =
|A| =
= 1 (3 – 1) – 1 (-6 – 2) + 1 (2 + 2)
= 2 + 8 + 4
= 14
Entonces, el sistema dado tiene una solución única dada por X = A -1 B.
Sean C ij los cofactores de los elementos a ij en A.
=
=
Ahora, X = A -1 B
=> x = -16/14, y = 20/14 y z = 38/14
Por tanto, x = -8/7, y = 10/7 y z = 19/7.
(iii) 6x − 12y + 25z = 4
4x + 15y − 20z = 3
2x + 18y + 15z = 10
Solución:
un =
|A| =
= 6 (225 + 360) + 12 (60 + 40) + 25 (72 – 30)
= 3510 + 1200 + 1050
= 5760
Entonces, el sistema dado tiene una solución única dada por X = A -1 B.
Sean C ij los cofactores de los elementos a ij en A.
=
=
Ahora, X = A -1 B
=> x = 2880/5760, y = 1920/5760 y z = 1152/5760
Por lo tanto x = 1/2, y = 1/3 y z = 1/5.
(iv) 3x + 4y + 7z = 14
2x – y + 3z = 4
x + 2y − 3z = 0
Solución:
un =
|A| =
= 3 (3 – 3) – 4 (- 6 – 6) + 7 (2 + 2)
= 0 + 48 + 28
= 76
Entonces, el sistema dado tiene una solución única dada por X = A -1 B.
Sean C ij los cofactores de los elementos a ij en A.
=
=
Ahora, X = A -1 B
=> x = 76/76, y = 76/76 y z = 76/76
Por lo tanto x = 1, y = 1 y z = 1.
(v) 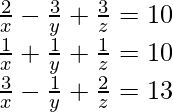
Solución:
Sean 1/x a, 1/y b y 1/z c.
Aquí,
un =
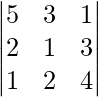
|A| =
= 2 (2 + 1) + 3 (2 – 3) + 3 (-1 – 3)
= 6 – 3 – 12
= -9
Entonces, el sistema dado tiene una solución única dada por X = A -1 B.
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
=> x = 1/a = – 9/-18, y = 1/b = – 9/- 27 y z = 1/c = -9/-45
Por lo tanto x = 1/2, y = 1/3 y z = 1/5.
(vi) 5x + 3y + z = 16
2x + y + 3z = 19
x + 2y + 4z = 25
Solución:
un =
|A| =
= 5 (4 – 6) – 3 (8 – 3) + 1 (4 – 1)
= -10 – 15 + 3
= – 22
Entonces, el sistema dado tiene una solución única dada por X = A -1 B.
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
=> x = – 22/- 22, y = – 44/- 22 y z = -110/-22
Por lo tanto x = 1, y = 2 y z = 5.
(vii) 3x + 4y + 2z = 8
2y − 3z = 3
x − 2y + 6z = −2
Solución:
un =
|A| =
= 3 (12 – 6) – 4 (0 + 3) + 2 (0 – 2)
= 18 – 12 – 4
= 2
Sean C ij los cofactores de los elementos a ij en A.
=
=
Ahora X = A -1 B
=> x = -4/2, y = 6/2 y z = 2/2
Por lo tanto x = -2, y = 3 y z = 1.
(viii) 2x + y + z = 2
x + 3y – z = 5
3x + y − 2z = 6
Solución:
Aquí,
un =
|A| =
= – 10 – 1 – 8
= -19
Sean C ij los cofactores de los elementos a ij en A.
adj A =
=
=
X = A -1B
x = -19/-19, y = -19/-19 y z = 19/-19
Por lo tanto x = 1, y = 1 y z = – 1.
(ix) 2x + 6y = 2
3x − z = −8
2x – y + z = -3
Solución:
un =
|A| =
= 2 (0 – 1) – 6 (3 + 2) + 0 (-3 + 0)
= -2 – 30
= – 32
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
=> x = 64/-32, y = -32/-32 y z = -64/-32
Por lo tanto x = – 2, y = 1 y z = 2.
(x) x – y + z = 2
2x − y = 0
2y − z = 1
Solución:
un =
|A| =
= 1 (1 – 0) + 1 (-2 – 0) + 1(4 – 0)
= 1 – 2 + 4
= 3
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
=> x = 3/3, y = 6/3 y z = 9/3
Por lo tanto x = 1, y = 2 y z = 3.
(xi) 8x + 4y + 3z = 18
2x + y +z = 5
x + 2y + z = 5
Solución:
un =
|A| =
= 8 (1 – 2) – 4 (2 – 1) + 3(4 – 1)
= – 8 – 4 + 9
= -3
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
=> x = -3/-3, y = -3/-3 y z = -6/-3
Por lo tanto x = 1, y = 1 y z = 2.
(xii) x + y + z = 6
x + 2z = 7
3x + y + z = 12
Solución:
un =
|A| =
= 1 (0 – 2) – 1 (1 – 6) + 1(1 – 0)
= – 2 + 5 + 1
= 4
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
=> x = 12/4, y = 4/4 y z = -20/4
Por lo tanto x = 3, y = 1 y z = – 5.
(xiii) 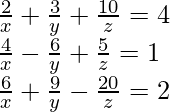 , x, y, z ≠ 0
, x, y, z ≠ 0
Solución:
Sean 1/x a, 1/y b y 1/z c.
Aquí,
un =
|A| =
= 2 (120 – 45) – 3 (-80 – 30) + 10 (36 + 36)
= 150 + 330 + 720
= 1200
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
=> x = 1/a = 1200/600, y = 1/b = 1200/400 y z = 1/c = 1200/240
Por lo tanto x = 2, y = 3 y z = 5.
(xiv) x − y + 2z = 7
3x + 4y − 5z = −5
2x – y + 3z = 12
Solución:
un =
|A| =
= 1 (12 – 5) + 1 (9 + 10) + 2 (-3 – 8)
= 7 + 19 – 22
= 4
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
=> x = 8/4, y = 4/4 y z = 12/4
Por lo tanto x = 2, y = 1 y z = 3.
Pregunta 3. Demuestre que los siguientes sistemas de ecuaciones lineales son consistentes:
(yo) 6x + 4y = 2
9x + 6y = 3
Solución:
Aquí,
6x + 4y = 2
9x + 6y = 3
Sabemos, AX = B
A =
, X =
y B =
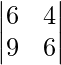
|A| =
= 36 – 36
= 0
Sean C ij los cofactores de los elementos a ij en A.
C 11 = 6, C 12 = -9, C 21 = -4 y C 22 = 6
=
(adj A) B =
=
=
Por lo tanto, el sistema es consistente y tiene infinitas soluciones.
Por lo tanto probado.
(ii) 2x + 3y = 5
6x + 9y = 15
Solución:
Aquí,
2x + 3y = 5
6x + 9y = 15
Sabemos, AX = B
A =
, X =
y B =
|A| =
= 18 – 18
= 0
Sean C ij los cofactores de los elementos a ij en A.
C 11 = 9, C 12 = -6, C 21 = -3 y C 22 = 2
=
(adj A) B =
=
=
Por lo tanto, el sistema es consistente y tiene infinitas soluciones.
Por lo tanto probado.
(iii) 5x + 3y + 7z = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
Solución:
Aquí,
5x + 3y + 7z = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
Sabemos, AX = B
A =
, X =
y B =
|A| =
= 1280 – 48 – 1232\]
= 0
Sean C ij los cofactores de los elementos a ij en A.
=
(adj. A)B =
=
=
Por lo tanto, el sistema es consistente y tiene infinitas soluciones.
Por lo tanto probado.
(iv) x – y + z = 3
2x + y − z = 2
−x −2y + 2z = 1
Solución:
Aquí,
x – y + z = 3
2x + y − z = 2
−x −2y + 2z = 1
Sabemos, AX = B
A =
, X =
y B =
|A| =
= 1\izquierda( 2 – 2 \derecha) + 1\izquierda( 4 – 1 \derecha) + 1( – 4 + 1)\]
= 0 + 3 – 3
= 0
Sean C ij los cofactores de los elementos a ij en A.
=
(adj A) B =
=
=
Por lo tanto, el sistema es consistente y tiene infinitas soluciones.
Por lo tanto probado.
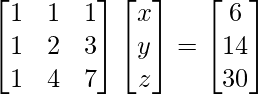
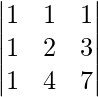
(v) x + y + z = 6
x + 2y + 3z = 14
x + 4y + 7z = 30
Solución:
Aquí,
x + y + z = 6
x + 2y + 3z = 14
x + 4y + 7z = 30
A =
, X =
y B =
|A| =
= 2 – 4 + 2
= 0
Sean C ij los cofactores de los elementos a ij en A.
=
=
=
Por lo tanto, el sistema es consistente y tiene infinitas soluciones.
Por lo tanto probado.
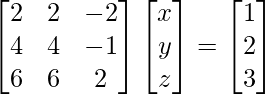
(vi) 2x + 2y − 2z = 1
4x + 4y – z = 2
6x + 6y + 2z = 3
Solución:
Aquí,
2x + 2y − 2z = 1
4x + 4y – z = 2
6x + 6y + 2z = 3
A =
, X =
y B =
|A| =
= 2 (8 + 6) – 2 (8 + 6) – 2 (24 – 24)
= 28 – 28 – 0
= 0
Sean C ij los cofactores de los elementos a ij en A.
=
(adj A) B =
=
=
Por lo tanto, el sistema es consistente y tiene infinitas soluciones.
Por lo tanto probado.
Pregunta 4. Demostrar que cada uno de los siguientes sistemas de ecuaciones lineales es inconsistente:
(yo) 2x + 5y = 7
6x + 15y = 13
Solución:
El sistema de ecuaciones dado se puede expresar de la siguiente manera:
AX = B
Aquí,
A =
, X =
y B =
Ahora,
|A| =
= 30 – 30
= 0
Sean C ij los cofactores de los elementos a ij en A.
C 11 = 15, C 12 = -6, C 21 = -5 y C 22 = 2
adj A =
=
(adj A) B =
=
=
≠ 0
Por lo tanto, el sistema de ecuaciones dado es inconsistente.
Por lo tanto probado.
(ii) 2x + 3y = 5
6x + 9y = 10
Solución:
El sistema de ecuaciones dado se puede expresar de la siguiente manera:
AX = B
Aquí,
A =
, X =
y B =
|A| =
= 18 – 18
= 0
Sean C ij los cofactores de los elementos a ij en A.
C 11 = 9, C 12 = -6, C 21 = -3 y C 22 = 2
=
(adj A) B =
=
=
≠ 0
Por lo tanto, el sistema de ecuaciones dado es inconsistente.
Por lo tanto probado.
(iii) 4x − 2y = 3
6x − 3y = 5
Solución:
El sistema de ecuaciones dado se puede expresar como,
AX = B
Aquí,
A =
, X =
y B =
|A| =
= 12 – 12
= 0
Sean C ij los cofactores de los elementos a ij en A.
C 11 = -3, C 12 = -6, C 21 = 2 y C 22 = 4
=
(adj A) B =
=
=
≠ 0
Por lo tanto, el sistema de ecuaciones dado es inconsistente.
Por lo tanto probado.
(iv) 4x − 5y − 2z = 2
5x − 4y + 2z = −2
2x + 2y + 8z = −1
Solución:
El sistema de ecuaciones dado se puede escribir como,
AX = B
Aquí,
A =
, X =
y B =
|A| =
= -144 + 180 – 36
= 0
Sean C ij los cofactores de los elementos a ij en A.
=
(adj A) B =
=
=
≠ 0
Por lo tanto, el sistema de ecuaciones dado es inconsistente.
Por lo tanto probado.
(v) 3x − y − 2z = 2
2y − z = −1
3x − 5y = 3
Solución:
El sistema de ecuaciones dado se puede escribir como,
AX = B
Aquí,
A =
, X =
y B =
|A| =
= -15 + 3 + 12
= 0
Sean C ij los cofactores de los elementos a ij en A.
adj A =
=
(adj A) B =
=
=
≠ 0
Por lo tanto, el sistema de ecuaciones dado es inconsistente.
Por lo tanto probado.
(vi) x + y − 2z = 5
x − 2y + z = −2
−2x + y + z = 4
Solución:
El sistema de ecuaciones dado se puede escribir como,
AX = B
Aquí,
A =
, X =
y B =
|A| =
= – 3 – 3 + 6
= 0
Sean C ij los cofactores de los elementos a ij en A.
=
(adj A) B =
=
=
≠ 0
Por lo tanto, el sistema de ecuaciones dado es inconsistente.
Por lo tanto probado.
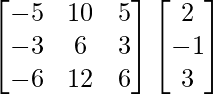
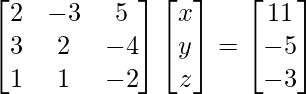
Pregunta 5. Si A = 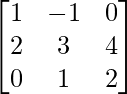 y B =
y B = 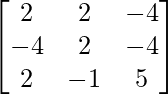 son dos arrays cuadradas, encuentre AB y, por lo tanto, resuelva el sistema de ecuaciones lineales: x − y = 3, 2x + 3y + 4z = 17, y + 2z = 7.
son dos arrays cuadradas, encuentre AB y, por lo tanto, resuelva el sistema de ecuaciones lineales: x − y = 3, 2x + 3y + 4z = 17, y + 2z = 7.
Solución:
Aquí,
A =
y B =
Ahora,
AB =
AB =
AB =
AB = 6I
= yo
X = A -1B
X =
Por lo tanto x = 2, y = -1 y z = 4.
Pregunta 6. Si A = 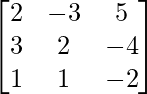 , encuentre A −1 y, por lo tanto, resuelva el sistema de ecuaciones lineales 2x − 3y + 5z = 11, 3x + 2y − 4z = −5, x + y + 2z = −3.
, encuentre A −1 y, por lo tanto, resuelva el sistema de ecuaciones lineales 2x − 3y + 5z = 11, 3x + 2y − 4z = −5, x + y + 2z = −3.
Solución:
Aquí,
un =
|A| =
= 0 – 6 + 5
= -1
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
=> x = – 1/- 1, y = -2/-1\ y z = -3/-1
Por lo tanto x = 1, y = 2 y z = 3.
Pregunta 7. Encuentra A −1 , si A = 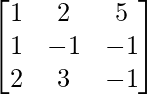 . Por tanto, resuelve el siguiente sistema de ecuaciones lineales: x + 2y + 5z = 10, x − y − z = −2, 2x + 3y − z = −11.
. Por tanto, resuelve el siguiente sistema de ecuaciones lineales: x + 2y + 5z = 10, x − y − z = −2, 2x + 3y − z = −11.
Solución:
un =
|A| =
= 4 – 2 + 25
= 27
Sean C ij los cofactores de los elementos a ij en A.
=
=
X = A -1B
=> x = -27/27, y = -54/27 y z = 81/27
Por lo tanto, x = – 1, y = -2 y z = 3.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA