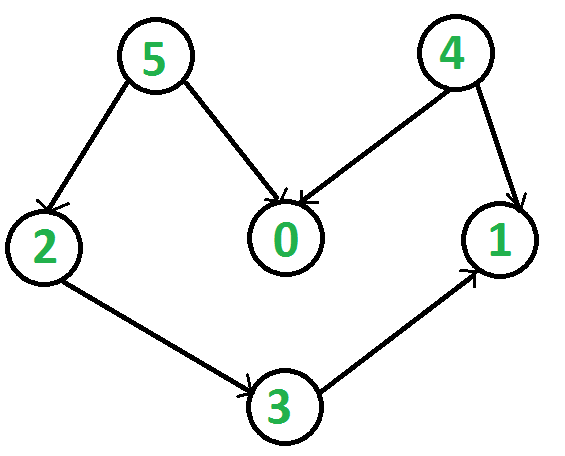
La ordenación topológica para el gráfico acíclico dirigido (DAG) es una ordenación lineal de vértices tal que para cada arista dirigida uv, el vértice u viene antes que v en la ordenación. La clasificación topológica de un gráfico no es posible si el gráfico no es un DAG.
Por ejemplo, una clasificación topológica del siguiente gráfico es «5 4 2 3 1 0». Puede haber más de una clasificación topológica para un gráfico. Por ejemplo, otra clasificación topológica del siguiente gráfico es «4 5 2 3 1 0». El primer vértice en la clasificación topológica siempre es un vértice con grado de entrada 0 (un vértice sin bordes entrantes).
Clasificación topológica frente a profundidad primero transversal (DFS) :
En DFS , imprimimos un vértice y luego recursivamente llamamos a DFS para sus vértices adyacentes. En la clasificación topológica, necesitamos imprimir un vértice antes que sus vértices adyacentes. Por ejemplo, en el gráfico dado, el vértice ‘5’ debe imprimirse antes del vértice ‘0’, pero a diferencia de DFS , el vértice ‘4’ también debe imprimirse antes del vértice ‘0’. Entonces, la clasificación topológica es diferente de DFS. Por ejemplo, un DFS del gráfico que se muestra es «5 2 3 1 0 4», pero no es una clasificación topológica.
Algoritmo para encontrar la clasificación topológica:
Recomendamos ver primero la implementación de DFS . Podemos modificar DFS para encontrar la clasificación topológica de un gráfico. En DFS , comenzamos desde un vértice, primero lo imprimimos y luego recursivamente llamamos a DFS para sus vértices adyacentes. En la clasificación topológica, usamos una pila temporal. No imprimimos el vértice de inmediato, primero llamamos recursivamente a la clasificación topológica para todos sus vértices adyacentes y luego lo colocamos en una pila. Finalmente, imprima el contenido de la pila. Tenga en cuenta que un vértice se empuja a la pila solo cuando todos sus vértices adyacentes (y sus vértices adyacentes, etc.) ya están en la pila.
La siguiente imagen es una ilustración del enfoque anterior:

A continuación se muestran las implementaciones de clasificación topológica. Consulte el código de profundidad de primer recorrido para un gráfico desconectado y tenga en cuenta las diferencias entre el segundo código que se proporciona allí y el siguiente código.
C++
// A C++ program to print topological
// sorting of a DAG
#include <iostream>
#include <list>
#include <stack>
using namespace std;
// Class to represent a graph
class Graph {
// No. of vertices'
int V;
// Pointer to an array containing adjacency listsList
list<int>* adj;
// A function used by topologicalSort
void topologicalSortUtil(int v, bool visited[],
stack<int>& Stack);
public:
// Constructor
Graph(int V);
// function to add an edge to graph
void addEdge(int v, int w);
// prints a Topological Sort of
// the complete graph
void topologicalSort();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
// Add w to v’s list.
adj[v].push_back(w);
}
// A recursive function used by topologicalSort
void Graph::topologicalSortUtil(int v, bool visited[],
stack<int>& Stack)
{
// Mark the current node as visited.
visited[v] = true;
// Recur for all the vertices
// adjacent to this vertex
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
topologicalSortUtil(*i, visited, Stack);
// Push current vertex to stack
// which stores result
Stack.push(v);
}
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
void Graph::topologicalSort()
{
stack<int> Stack;
// Mark all the vertices as not visited
bool* visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// Call the recursive helper function
// to store Topological
// Sort starting from all
// vertices one by one
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortUtil(i, visited, Stack);
// Print contents of stack
while (Stack.empty() == false) {
cout << Stack.top() << " ";
Stack.pop();
}
}
// Driver Code
int main()
{
// Create a graph given in the above diagram
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
cout << "Following is a Topological Sort of the given "
"graph \n";
// Function Call
g.topologicalSort();
return 0;
}
Java
// A Java program to print topological
// sorting of a DAG
import java.io.*;
import java.util.*;
// This class represents a directed graph
// using adjacency list representation
class Graph {
// No. of vertices
private int V;
// Adjacency List as ArrayList of ArrayList's
private ArrayList<ArrayList<Integer> > adj;
// Constructor
Graph(int v)
{
V = v;
adj = new ArrayList<ArrayList<Integer> >(v);
for (int i = 0; i < v; ++i)
adj.add(new ArrayList<Integer>());
}
// Function to add an edge into the graph
void addEdge(int v, int w) { adj.get(v).add(w); }
// A recursive function used by topologicalSort
void topologicalSortUtil(int v, boolean visited[],
Stack<Integer> stack)
{
// Mark the current node as visited.
visited[v] = true;
Integer i;
// Recur for all the vertices adjacent
// to thisvertex
Iterator<Integer> it = adj.get(v).iterator();
while (it.hasNext()) {
i = it.next();
if (!visited[i])
topologicalSortUtil(i, visited, stack);
}
// Push current vertex to stack
// which stores result
stack.push(new Integer(v));
}
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
void topologicalSort()
{
Stack<Integer> stack = new Stack<Integer>();
// Mark all the vertices as not visited
boolean visited[] = new boolean[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// Call the recursive helper
// function to store
// Topological Sort starting
// from all vertices one by one
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortUtil(i, visited, stack);
// Print contents of stack
while (stack.empty() == false)
System.out.print(stack.pop() + " ");
}
// Driver code
public static void main(String args[])
{
// Create a graph given in the above diagram
Graph g = new Graph(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
System.out.println("Following is a Topological "
+ "sort of the given graph");
// Function Call
g.topologicalSort();
}
}
// This code is contributed by Aakash Hasija
Python3
# Python program to print topological sorting of a DAG
from collections import defaultdict
# Class to represent a graph
class Graph:
def __init__(self, vertices):
self.graph = defaultdict(list) # dictionary containing adjacency List
self.V = vertices # No. of vertices
# function to add an edge to graph
def addEdge(self, u, v):
self.graph[u].append(v)
# A recursive function used by topologicalSort
def topologicalSortUtil(self, v, visited, stack):
# Mark the current node as visited.
visited[v] = True
# Recur for all the vertices adjacent to this vertex
for i in self.graph[v]:
if visited[i] == False:
self.topologicalSortUtil(i, visited, stack)
# Push current vertex to stack which stores result
stack.append(v)
# The function to do Topological Sort. It uses recursive
# topologicalSortUtil()
def topologicalSort(self):
# Mark all the vertices as not visited
visited = [False]*self.V
stack = []
# Call the recursive helper function to store Topological
# Sort starting from all vertices one by one
for i in range(self.V):
if visited[i] == False:
self.topologicalSortUtil(i, visited, stack)
# Print contents of the stack
print(stack[::-1]) # return list in reverse order
# Driver Code
g = Graph(6)
g.addEdge(5, 2)
g.addEdge(5, 0)
g.addEdge(4, 0)
g.addEdge(4, 1)
g.addEdge(2, 3)
g.addEdge(3, 1)
print ("Following is a Topological Sort of the given graph")
# Function Call
g.topologicalSort()
# This code is contributed by Neelam Yadav
C#
// A C# program to print topological
// sorting of a DAG
using System;
using System.Collections.Generic;
// This class represents a directed graph
// using adjacency list representation
class Graph {
// No. of vertices
private int V;
// Adjacency List as ArrayList
// of ArrayList's
private List<List<int> > adj;
// Constructor
Graph(int v)
{
V = v;
adj = new List<List<int> >(v);
for (int i = 0; i < v; i++)
adj.Add(new List<int>());
}
// Function to add an edge into the graph
public void AddEdge(int v, int w) { adj[v].Add(w); }
// A recursive function used by topologicalSort
void TopologicalSortUtil(int v, bool[] visited,
Stack<int> stack)
{
// Mark the current node as visited.
visited[v] = true;
// Recur for all the vertices
// adjacent to this vertex
foreach(var vertex in adj[v])
{
if (!visited[vertex])
TopologicalSortUtil(vertex, visited, stack);
}
// Push current vertex to
// stack which stores result
stack.Push(v);
}
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
void TopologicalSort()
{
Stack<int> stack = new Stack<int>();
// Mark all the vertices as not visited
var visited = new bool[V];
// Call the recursive helper function
// to store Topological Sort starting
// from all vertices one by one
for (int i = 0; i < V; i++) {
if (visited[i] == false)
TopologicalSortUtil(i, visited, stack);
}
// Print contents of stack
foreach(var vertex in stack)
{
Console.Write(vertex + " ");
}
}
// Driver code
public static void Main(string[] args)
{
// Create a graph given
// in the above diagram
Graph g = new Graph(6);
g.AddEdge(5, 2);
g.AddEdge(5, 0);
g.AddEdge(4, 0);
g.AddEdge(4, 1);
g.AddEdge(2, 3);
g.AddEdge(3, 1);
Console.WriteLine("Following is a Topological "
+ "sort of the given graph");
// Function Call
g.TopologicalSort();
}
}
// This code is contributed by Abhinav Galodha
Javascript
<script>
// Javascript for the above approach
// This class represents a directed graph
// using adjacency list representation
class Graph{
// Constructor
constructor(v)
{
// Number of vertices
this.V = v
// Adjacency List as ArrayList of ArrayList's
this.adj = new Array(this.V)
for (let i = 0 ; i < this.V ; i+=1){
this.adj[i] = new Array()
}
}
// Function to add an edge into the graph
addEdge(v, w){
this.adj[v].push(w)
}
// A recursive function used by topologicalSort
topologicalSortUtil(v, visited, stack)
{
// Mark the current node as visited.
visited[v] = true;
let i = 0;
// Recur for all the vertices adjacent
// to thisvertex
for(i = 0 ; i < this.adj[v].length ; i++){
if(!visited[this.adj[v][i]]){
this.topologicalSortUtil(this.adj[v][i], visited, stack)
}
}
// Push current vertex to stack
// which stores result
stack.push(v);
}
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
topologicalSort()
{
let stack = new Array()
// Mark all the vertices as not visited
let visited = new Array(this.V);
for (let i = 0 ; i < this.V ; i++){
visited[i] = false;
}
// Call the recursive helper
// function to store
// Topological Sort starting
// from all vertices one by one
for (let i = 0 ; i < this.V ; i++){
if (visited[i] == false){
this.topologicalSortUtil(i, visited, stack);
}
}
// Print contents of stack
while (stack.length != 0){
console.log(stack.pop() + " ")
}
}
}
// Driver Code
var g = new Graph(6)
g.addEdge(5, 2)
g.addEdge(5, 0)
g.addEdge(4, 0)
g.addEdge(4, 1)
g.addEdge(2, 3)
g.addEdge(3, 1)
console.log("Following is a Topological sort of the given graph")
// Function Call
g.topologicalSort()
// This code is contributed by subhamgoyal2014.
</script>
Following is a Topological Sort of the given graph 5 4 2 3 1 0
Análisis de Complejidad:
- Complejidad Temporal: O(V+E).
El algoritmo anterior es simplemente DFS con una pila extra. Entonces, la complejidad del tiempo es la misma que la DFS, que es. - Espacio auxiliar: O(V).
El espacio extra es necesario para la pila.
Nota: Aquí, también podemos usar vector en lugar de la pila. Si se usa el vector, imprima los elementos en orden inverso para obtener la clasificación topológica.
Aplicaciones:
la clasificación topológica se utiliza principalmente para programar trabajos a partir de las dependencias dadas entre trabajos. En informática, las aplicaciones de este tipo surgen en la programación de instrucciones, el ordenamiento de la evaluación de celdas de fórmulas al volver a calcular los valores de fórmulas en hojas de cálculo, la síntesis lógica, la determinación del orden de las tareas de compilación a realizar en archivos make, la serialización de datos y la resolución de dependencias de símbolos en enlazadores [ 2 ].
Artículos relacionados:
Algoritmo de Kahn para clasificación topológica : otro algoritmo O(V + E).
Todos los tipos topológicos de un gráfico acíclico dirigido
Referencias:
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/GraphAlgor/topoSort.htm
http://en.wikipedia.org/wiki/Topological_sorting
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA