Dado un gráfico acíclico dirigido (DAG), encuentre la ordenación topológica del gráfico.
La ordenación topológica para el gráfico acíclico dirigido (DAG) es una ordenación lineal de vértices tal que para cada arista dirigida uv, el vértice u viene antes que v en la ordenación. La clasificación topológica de un gráfico no es posible si el gráfico no es un DAG.
Por ejemplo, una clasificación topológica del siguiente gráfico es «5 4 2 3 1 0». Puede haber más de una clasificación topológica para un gráfico. Por ejemplo, otra ordenación topológica del siguiente gráfico es “4 5 2 3 1 0”.
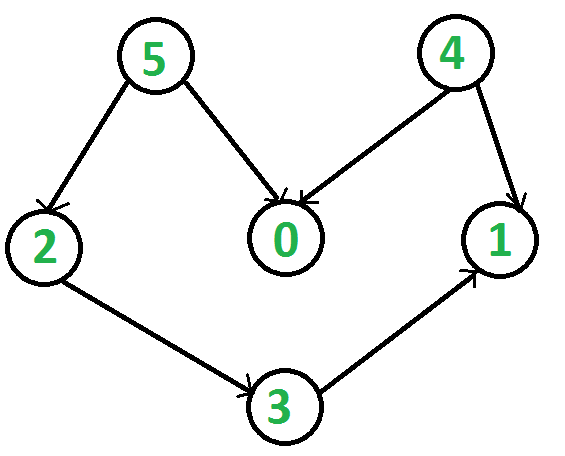
Tenga en cuenta que el primer vértice en la clasificación topológica siempre es un vértice con grado de entrada 0 (un vértice sin bordes entrantes). Para el gráfico anterior, los vértices 4 y 5 no tienen bordes entrantes.
Ya hemos discutido un algoritmo basado en DFS usando stack y el algoritmo de Kahn para clasificación topológica. También hemos discutido cómo imprimir todos los tipos topológicos del DAG aquí . En esta publicación, se analiza otro enfoque basado en DFS para encontrar el tipo topológico de un gráfico mediante la introducción del concepto de tiempo de llegada y salida de un vértice en DFS.
¿Cuál es la hora de llegada y la hora de salida de los vértices en DFS?
En DFS, Arrival Time es el momento en que se exploró el vértice por primera vez y Departure Time es el momento en que hemos explorado todos los vecinos del vértice y estamos listos para retroceder.
¿Cómo encontrar el tipo topológico de un gráfico usando la hora de salida?
Para encontrar la ordenación topológica de un gráfico, ejecutamos DFS a partir de todos los vértices no visitados uno por uno. Para cualquier vértice, antes de explorar cualquiera de sus vecinos, anotamos la hora de llegada de ese vértice y después de explorar todos los vecinos del vértice, anotamos su hora de salida. Tenga en cuenta que solo se necesita la hora de salida para encontrar la clasificación topológica de un gráfico, por lo que podemos omitir la hora de llegada del vértice. Finalmente, después de haber visitado todos los vértices del gráfico, imprimimos los vértices en orden decreciente de tiempo de salida, que es nuestro orden topológico de vértices deseado.
A continuación se muestra la implementación en C++ de la idea anterior:
C++
// A C++ program to print topological sorting of a DAG
#include <bits/stdc++.h>
using namespace std;
// Graph class represents a directed graph using adjacency
// list representation
class Graph {
int V; // No. of vertices
// Pointer to an array containing adjacency lists
list<int>* adj;
public:
Graph(int); // Constructor
~Graph(); // Destructor
// function to add an edge to graph
void addEdge(int, int);
// The function to do DFS traversal
void DFS(int, vector<bool>&, vector<int>&, int&);
// The function to do Topological Sort.
void topologicalSort();
};
Graph::Graph(int V)
{
this->V = V;
this->adj = new list<int>[V];
}
Graph::~Graph() { delete[] this->adj; }
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // Add w to v's list.
}
// The function to do DFS() and stores departure time
// of all vertex
void Graph::DFS(int v, vector<bool>& visited,
vector<int>& departure, int& time)
{
visited[v] = true;
// time++; // arrival time of vertex v
for (int i : adj[v])
if (!visited[i])
DFS(i, visited, departure, time);
// set departure time of vertex v
departure[time++] = v;
}
// The function to do Topological Sort. It uses DFS().
void Graph::topologicalSort()
{
// vector to store departure time of vertex.
vector<int> departure(V, -1);
// Mark all the vertices as not visited
vector<bool> visited(V, false);
int time = 0;
// perform DFS on all unvisited vertices
for (int i = 0; i < V; i++) {
if (visited[i] == 0) {
DFS(i, visited, departure, time);
}
}
// print the topological sort
for (int i = V - 1; i >= 0; i--)
cout << departure[i] << " ";
}
// Driver program to test above functions
int main()
{
// Create a graph given in the above diagram
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
cout << "Topological Sort of the given graph is \n";
g.topologicalSort();
return 0;
}
Python3
# A Python3 program to print topological sorting of a DAG
def addEdge(u, v):
global adj
adj[u].append(v)
# The function to do DFS() and stores departure time
# of all vertex
def DFS(v):
global visited, departure, time
visited[v] = 1
for i in adj[v]:
if visited[i] == 0:
DFS(i)
departure[time] = v
time += 1
# The function to do Topological Sort. It uses DFS().
def topologicalSort():
# perform DFS on all unvisited vertices
for i in range(V):
if(visited[i] == 0):
DFS(i)
# Print vertices in topological order
for i in range(V - 1, -1, -1):
print(departure[i], end = " ")
# Driver code
if __name__ == '__main__':
# Create a graph given in the above diagram
V,time, adj, visited, departure = 6, 0, [[] for i in range(7)], [0 for i in range(7)],[-1 for i in range(7)]
addEdge(5, 2)
addEdge(5, 0)
addEdge(4, 0)
addEdge(4, 1)
addEdge(2, 3)
addEdge(3, 1)
print("Topological Sort of the given graph is")
topologicalSort()
# This code is contributed by mohit kumar 29
C#
// C# program to print topological sorting of a DAG
using System;
using System.Collections.Generic;
// Graph class represents a directed graph using adjacency
// list representation
public class Graph {
private int V;
private List<int>[] adj;
// constructor
public Graph(int v)
{
V = v;
adj = new List<int>[ v ];
for (int i = 0; i < v; i++)
adj[i] = new List<int>();
}
// Add an edge
public void AddEdge(int v, int w)
{
adj[v].Add(w); // Add w to v's list
}
// The function to do DFS() and stores departure time
// of all vertex
private void DFS(int v, bool[] visited, int[] departure,
ref int time)
{
visited[v] = true;
// time++; // arrival time of vertex v
foreach(int i in adj[v])
{
if (!visited[i])
DFS(i, visited, departure, ref time);
}
// set departure time of vertex v
departure[time++] = v;
}
// The function to do Topological Sort. It uses DFS().
public void TopologicalSort()
{
// vector to store departure time of vertex.
int[] departure = new int[V];
for (int i = 0; i < V; i++)
departure[i] = -1;
// Mark all the vertices as not visited
bool[] visited = new bool[V];
int time = 0;
// perform DFS on all unvisited vertices
for (int i = 0; i < V; i++) {
if (visited[i] == false) {
DFS(i, visited, departure, ref time);
}
}
// print the topological sort
for (int i = V - 1; i >= 0; i--)
Console.Write(departure[i] + " ");
Console.WriteLine();
}
}
class GFG {
// Driver program to test above functions
static void Main(string[] args)
{
// Create a graph given in the above diagram
Graph g = new Graph(6);
g.AddEdge(5, 2);
g.AddEdge(5, 0);
g.AddEdge(4, 0);
g.AddEdge(4, 1);
g.AddEdge(2, 3);
g.AddEdge(3, 1);
Console.WriteLine(
"Topological Sort of the given graph is");
g.TopologicalSort();
}
}
// This code is contributed by cavi4762
Javascript
<script>
// A JavaScript program to print topological
// sorting of a DAG
let adj=new Array(7);
for(let i=0;i<adj.length;i++)
{
adj[i]=[];
}
let V=6;
let time=0;
let visited=new Array(7);
let departure =new Array(7);
for(let i=0;i<7;i++)
{
visited[i]=0;
departure[i]=-1;
}
function addEdge(u, v)
{
adj[u].push(v)
}
// The function to do DFS() and
// stores departure time
// of all vertex
function DFS(v)
{
visited[v] = 1;
for(let i=0;i<adj[v].length;i++)
{
if(visited[adj[v][i]]==0)
DFS(adj[v][i]);
}
departure[time] = v
time += 1
}
// The function to do Topological
// Sort. It uses DFS().
function topologicalSort()
{
//perform DFS on all unvisited vertices
for(let i=0;i<V;i++)
{
if(visited[i] == 0)
DFS(i)
}
//perform DFS on all unvisited vertices
for(let i=V-1;i>=0;i--)
{
document.write(departure[i]+" ");
}
}
// Create a graph given in the above diagram
addEdge(5, 2);
addEdge(5, 0);
addEdge(4, 0);
addEdge(4, 1);
addEdge(2, 3);
addEdge(3, 1);
document.write(
"Topological Sort of the given graph is<br>"
);
topologicalSort()
// This code is contributed by unknown2108
</script>
Topological Sort of the given graph is 5 4 2 3 1 0
La complejidad temporal de la solución anterior es O(V + E).
Este artículo es una contribución de Aditya Goel . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA