Requisito previo: HeapSort
Heap sort es una técnica de clasificación basada en comparación basada en la estructura de datos de Binary Heap . Es similar a la ordenación por selección donde primero encontramos el elemento máximo y colocamos el elemento máximo al final. Repetimos el mismo proceso para el elemento restante.
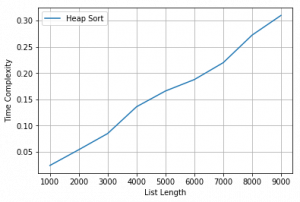
Implementamos Heap Sort aquí, lo llamamos para listas aleatorias de diferentes tamaños, medimos el tiempo necesario para diferentes tamaños y generamos un gráfico de tamaño de entrada frente al tiempo necesario.
Python
# Python Code for Implementation and running time Algorithm
# Complexity plot of Heap Sort
# by Ashok Kajal
# This python code intends to implement Heap Sort Algorithm
# Plots its time Complexity on list of different sizes
# ---------------------Important Note -------------------
# numpy, time and matplotlib.pyplot are required to run this code
import time
from numpy.random import seed
from numpy.random import randint
import matplotlib.pyplot as plt
# find left child of node i
def left(i):
return 2 * i + 1
# find right child of node i
def right(i):
return 2 * i + 2
# calculate and return array size
def heapSize(A):
return len(A)-1
# This function takes an array and Heapyfies
# the at node i
def MaxHeapify(A, i):
# print("in heapy", i)
l = left(i)
r = right(i)
# heapSize = len(A)
# print("left", l, "Rightt", r, "Size", heapSize)
if l<= heapSize(A) and A[l] > A[i] :
largest = l
else:
largest = i
if r<= heapSize(A) and A[r] > A[largest]:
largest = r
if largest != i:
# print("Largest", largest)
A[i], A[largest]= A[largest], A[i]
# print("List", A)
MaxHeapify(A, largest)
# this function makes a heapified array
def BuildMaxHeap(A):
for i in range(int(heapSize(A)/2)-1, -1, -1):
MaxHeapify(A, i)
# Sorting is done using heap of array
def HeapSort(A):
BuildMaxHeap(A)
B = list()
heapSize1 = heapSize(A)
for i in range(heapSize(A), 0, -1):
A[0], A[i]= A[i], A[0]
B.append(A[heapSize1])
A = A[:-1]
heapSize1 = heapSize1-1
MaxHeapify(A, 0)
# randomly generates list of different
# sizes and call HeapSort function
elements = list()
times = list()
for i in range(1, 10):
# generate some integers
a = randint(0, 1000 * i, 1000 * i)
# print(i)
start = time.clock()
HeapSort(a)
end = time.clock()
# print("Sorted list is ", a)
print(len(a), "Elements Sorted by HeapSort in ", end-start)
elements.append(len(a))
times.append(end-start)
plt.xlabel('List Length')
plt.ylabel('Time Complexity')
plt.plot(elements, times, label ='Heap Sort')
plt.grid()
plt.legend()
plt.show()
# This code is contributed by Ashok Kajal
Producción :
Input : Unsorted Lists of Different sizes are Generated Randomly Output : 1000 Elements Sorted by HeapSort in 0.023797415087301488 2000 Elements Sorted by HeapSort in 0.053856713614550245 3000 Elements Sorted by HeapSort in 0.08474737185133563 4000 Elements Sorted by HeapSort in 0.13578669978414837 5000 Elements Sorted by HeapSort in 0.1658182863213824 6000 Elements Sorted by HeapSort in 0.1875901601906662 7000 Elements Sorted by HeapSort in 0.21982946862249264 8000 Elements Sorted by HeapSort in 0.2724293921580738 9000 Elements Sorted by HeapSort in 0.30996323029421546 Complexity PLot for Heap Sort is Given Below