El código Hamming es un conjunto de códigos de corrección de errores que se pueden usar para detectar y corregir los errores que pueden ocurrir cuando los datos se mueven o almacenan del remitente al receptor. Es una técnica desarrollada por RW Hamming para la corrección de errores .
Bits redundantes –
Los bits redundantes son bits binarios adicionales que se generan y agregan a los bits de transferencia de datos que transportan información para garantizar que no se pierdan bits durante la transferencia de datos.
El número de bits redundantes se puede calcular utilizando la siguiente fórmula:
2^r ≥ m + r + 1 where, r = redundant bit, m = data bit
Supongamos que la cantidad de bits de datos es 7, entonces la cantidad de bits redundantes se puede calcular usando:
= 2^4 ≥ 7 + 4 + 1
Por lo tanto, la cantidad de bits redundantes = 4
Bits de paridad:
un bit de paridad se agrega a un dato de bits binarios para garantizar que el número total de 1 en los datos sea par o impar. Los bits de paridad se utilizan para la detección de errores. Hay dos tipos de bits de paridad:
- Bit de paridad par:
en el caso de paridad par, para un conjunto dado de bits, se cuenta el número de 1. Si ese recuento es impar, el valor del bit de paridad se establece en 1, lo que hace que el recuento total de ocurrencias de 1 sea un número par. Si el número total de 1 en un conjunto dado de bits ya es par, el valor del bit de paridad es 0. - Bit de paridad impar:
en el caso de paridad impar, para un conjunto dado de bits, se cuenta el número de 1. Si ese recuento es par, el valor del bit de paridad se establece en 1, lo que hace que el recuento total de ocurrencias de 1 sea un número impar. Si el número total de 1 en un conjunto dado de bits ya es impar, el valor del bit de paridad es 0.
Algoritmo general del código de Hamming:
el código de Hamming es simplemente el uso de bits de paridad adicionales para permitir la identificación de un error.
- Escriba las posiciones de bit a partir de 1 en forma binaria (1, 10, 11, 100, etc.).
- Todas las posiciones de bits que son una potencia de 2 se marcan como bits de paridad (1, 2, 4, 8, etc.).
- Todas las demás posiciones de bits están marcadas como bits de datos.
- Cada bit de datos se incluye en un conjunto único de bits de paridad, según determina su posición de bit en forma binaria.
una. El bit de paridad 1 cubre todas las posiciones de bits cuya representación binaria incluye un 1 en la
posición menos significativa (1, 3, 5, 7, 9, 11, etc).
b. El bit de paridad 2 cubre todas las posiciones de bits cuya representación binaria incluye un 1 en la segunda posición desde
el bit menos significativo (2, 3, 6, 7, 10, 11, etc).
C. El bit de paridad 4 cubre todas las posiciones de bits cuya representación binaria incluye un 1 en la tercera posición desde
el bit menos significativo (4–7, 12–15, 20–23, etc.).
d. El bit de paridad 8 cubre todas las posiciones de bits cuya representación binaria incluye un 1 en la cuarta posición desde
los bits menos significativos (8–15, 24–31, 40–47, etc.).
mi. En general, cada bit de paridad cubre todos los bits donde el AND bit a bit de la posición de paridad y la posición del bit
no es cero. - Dado que verificamos la paridad par, establezca un bit de paridad en 1 si el número total de unos en las posiciones que verifica es
impar. - Establezca un bit de paridad en 0 si el número total de unos en las posiciones que comprueba es par.

Determinación de la posición de los bits redundantes:
estos bits de redundancia se colocan en las posiciones que corresponden a la potencia de 2.
Como en el ejemplo anterior:
- El número de bits de datos = 7
- El número de bits redundantes = 4
- El número total de bits = 11
- Los bits redundantes se colocan en posiciones correspondientes a la potencia de 2- 1, 2, 4 y 8

Supongamos que el dato a transmitir es 1011001, los bits se colocarán de la siguiente manera:

Determinación de los bits de paridad –
- El bit R1 se calcula utilizando la verificación de paridad en todas las posiciones de bits cuya representación binaria incluye un 1 en la posición menos significativa.
R1: bits 1, 3, 5, 7, 9, 11
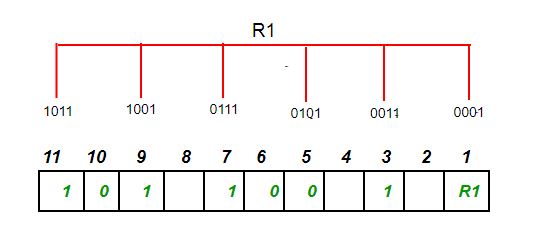
Para encontrar el bit redundante R1, verificamos la paridad. Dado que el número total de 1 en todas las posiciones de bit correspondientes a R1 es un número par, el valor de R1 (valor del bit de paridad) = 0
- El bit R2 se calcula utilizando la verificación de paridad en todas las posiciones de bits cuya representación binaria incluye un 1 en la segunda posición desde el bit menos significativo.
R2: bits 2,3,6,7,10,11

Para encontrar el bit redundante R2, verificamos la paridad. Dado que el número total de 1 en todas las posiciones de bits correspondientes a R2 es impar, el valor de R2 (valor del bit de paridad) = 1
- El bit R4 se calcula utilizando la verificación de paridad en todas las posiciones de bits cuya representación binaria incluye un 1 en la tercera posición desde el bit menos significativo.
R4: bits 4, 5, 6, 7

Para encontrar el bit redundante R4, verificamos la paridad. Dado que el número total de 1 en todas las posiciones de bits correspondientes a R4 es impar, el valor de R4 (valor del bit de paridad) = 1
- El bit R8 se calcula utilizando la verificación de paridad en todas las posiciones de bits cuya representación binaria incluye un 1 en la cuarta posición desde el bit menos significativo.
R8: bit 8,9,10,11

Para encontrar el bit redundante R8, verificamos la paridad. Dado que el número total de 1 en todas las posiciones de bit correspondientes a R8 es un número par, el valor de R8 (valor del bit de paridad) = 0.
Así, los datos transferidos son:

Detección y corrección de errores:
suponga que en el ejemplo anterior, el sexto bit se cambia de 0 a 1 durante la transmisión de datos, luego da nuevos valores de paridad en el número binario:
 ‘
‘
Los bits dan el número binario 0110 cuya representación decimal es 6. Por lo tanto, el bit 6 contiene un error. Para corregir el error, el sexto bit se cambia de 1 a 0.
Publicación traducida automáticamente
Artículo escrito por Harshita Pandey y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA