Códigos de detección de errores: Método de bit de paridad

Códigos de detección de errores:
la información binaria se transfiere de un lugar a otro a través de algún medio de comunicación. El ruido externo puede cambiar los bits de 1 a 0 o de 0 a 1. Estos cambios en los valores se denominan errores. Para una transferencia de datos eficiente, debe haber una detección de errores y códigos de corrección. Un código de detección de errores es un código binario que detecta errores digitales durante la transmisión. Un famoso código de detección de errores es un método de bits de paridad.

Método de bits de paridad:
un bit de paridad es un bit adicional incluido en un mensaje binario para hacer que el número total de 1 sea par o impar. La palabra de paridad denota el número de 1 en una string binaria. Hay dos sistemas de paridad, pares e impares. En el sistema de paridad par, 1 se agrega a la string binaria si hay un número impar de 1 en la string; de lo contrario, se agrega 0 para hacer un número par total de 1.

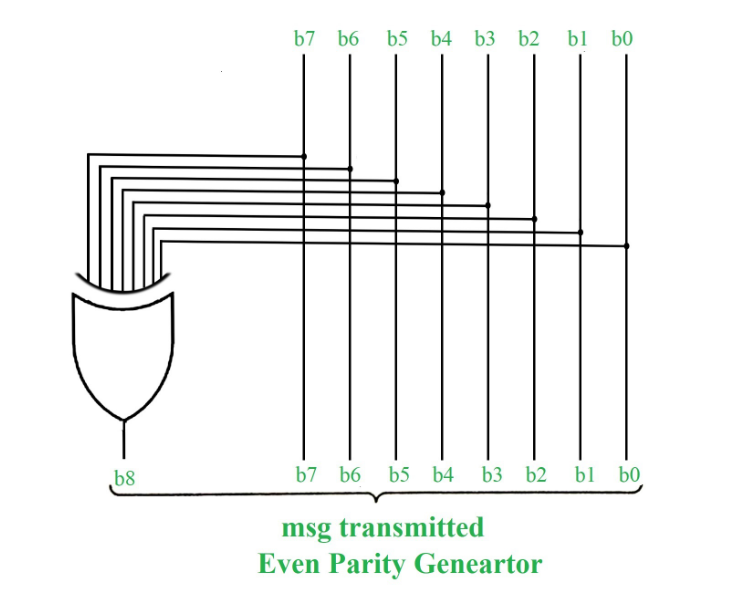
En el sistema de paridad impar, se agrega 1 a la string binaria si hay un número par de 1 para formar un número impar de 1. El receptor sabe si el remitente es un generador de paridad impar o un generador de paridad par. Supongamos que si el remitente es un generador de paridad impar, debe haber un número impar de 1 en la string binaria recibida. Si se produce un error en un solo bit que se cambia de 1 a 0 o de 0 a 1, el bit binario recibido tendrá un número par de 1, lo que indicará un error.

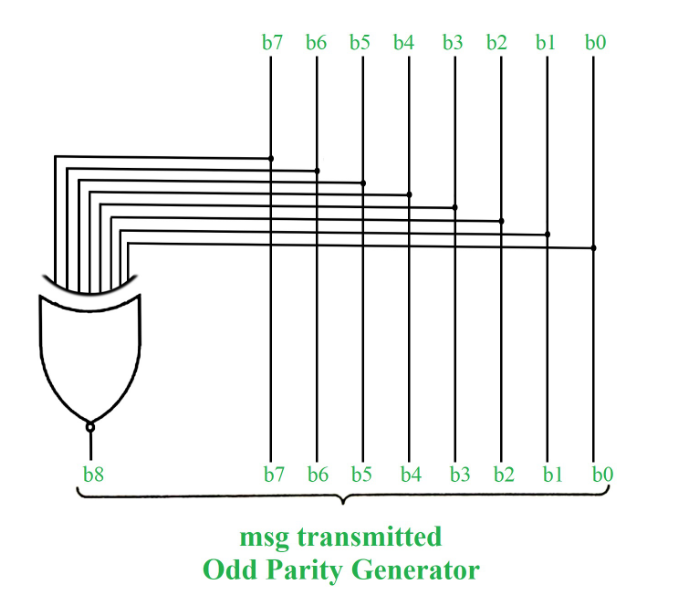
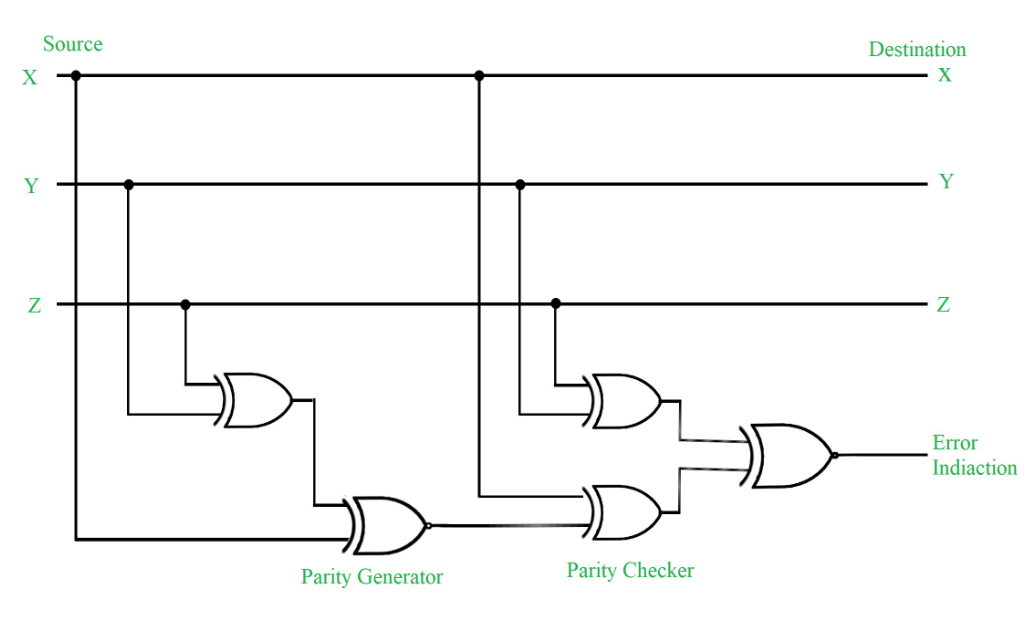
La limitación de este método es que solo se identificaría el error en un solo bit.

Mensaje (XYZ)	P(Impar)	P (par)
000	1	0
001	0	1
010	0	1
011	1	0
100	0	1
101	1	0
110	1	0
111	0	1

Figura: Detección de error con bit de paridad impar

Puntos para recordar :

• En el complemento a 1 del número con signo +0 y -0 tiene dos representaciones diferentes.
• El rango de representación de magnitud con signo de un número de 8 bits en el que 1 bit se usa como bit con signo de la siguiente manera -2 ⁷ a +2 ⁷ .
• Se dice que el número de punto flotante está normalizado si el dígito más significativo de la mantisa es uno. Por ejemplo, el número binario de 6 bits 001101 se normaliza debido a los dos ceros iniciales.
• El algoritmo de Booth que usa dos números de n bits para la multiplicación da resultados en 2n bits.
• El algoritmo de la cabina utiliza la representación de números en complemento a 2 y funciona tanto para números positivos como negativos.
• Si se utilizan k bits para representar el exponente, entonces el número de bits = (2 ^k-1 ) y el rango del exponente = – (2 ^k-1 -1) a (2 ^k -1).