El problema es opuesto a este post. Nos dan una estructura de datos de pila con operaciones push y pop, la tarea es implementar una cola usando instancias de estructura de datos de pila y operaciones en ellos.
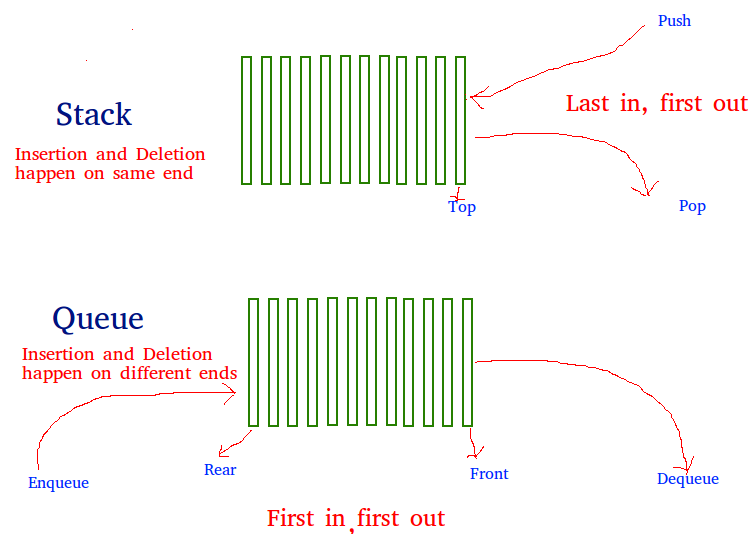
Una cola se puede implementar utilizando dos pilas. Deje que la cola que se implementará sea q y las pilas utilizadas para implementar q sean stack1 y stack2. q se puede implementar de dos maneras:
Método 1 (Al hacer que la operación enQueue sea costosa): este método se asegura de que el elemento ingresado más antiguo esté siempre en la parte superior de la pila 1, de modo que la operación de deQueue simplemente salte de la pila 1. Para poner el elemento en la parte superior de stack1, se usa stack2.
en cola (q, x):
- Si bien la pila 1 no está vacía, empuje todo, desde la pila 1 a la pila 2.
- Empuje x a stack1 (asumiendo que el tamaño de las pilas es ilimitado).
- Empuje todo de nuevo a stack1.
Aquí la complejidad del tiempo será O(n)
de cola (q):
- Si stack1 está vacío entonces error
- Extraiga un elemento de la pila 1 y devuélvalo
Aquí la complejidad del tiempo será O(1)
A continuación se muestra la implementación del enfoque anterior:
C++
// CPP program to implement Queue using
// two stacks with costly enQueue()
#include <bits/stdc++.h>
using namespace std;
struct Queue {
stack<int> s1, s2;
void enQueue(int x)
{
// Move all elements from s1 to s2
while (!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
// Push item into s1
s1.push(x);
// Push everything back to s1
while (!s2.empty()) {
s1.push(s2.top());
s2.pop();
}
}
// Dequeue an item from the queue
int deQueue()
{
// if first stack is empty
if (s1.empty()) {
cout << "Q is Empty";
exit(0);
}
// Return top of s1
int x = s1.top();
s1.pop();
return x;
}
};
// Driver code
int main()
{
Queue q;
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
return 0;
}
Java
// Java program to implement Queue using
// two stacks with costly enQueue()
import java.util.*;
class GFG
{
static class Queue
{
static Stack<Integer> s1 = new Stack<Integer>();
static Stack<Integer> s2 = new Stack<Integer>();
static void enQueue(int x)
{
// Move all elements from s1 to s2
while (!s1.isEmpty())
{
s2.push(s1.pop());
//s1.pop();
}
// Push item into s1
s1.push(x);
// Push everything back to s1
while (!s2.isEmpty())
{
s1.push(s2.pop());
//s2.pop();
}
}
// Dequeue an item from the queue
static int deQueue()
{
// if first stack is empty
if (s1.isEmpty())
{
System.out.println("Q is Empty");
System.exit(0);
}
// Return top of s1
int x = s1.peek();
s1.pop();
return x;
}
};
// Driver code
public static void main(String[] args)
{
Queue q = new Queue();
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
System.out.println(q.deQueue());
System.out.println(q.deQueue());
System.out.println(q.deQueue());
}
}
// This code is contributed by Prerna Saini
Python3
# Python3 program to implement Queue using
# two stacks with costly enQueue()
class Queue:
def __init__(self):
self.s1 = []
self.s2 = []
def enQueue(self, x):
# Move all elements from s1 to s2
while len(self.s1) != 0:
self.s2.append(self.s1[-1])
self.s1.pop()
# Push item into self.s1
self.s1.append(x)
# Push everything back to s1
while len(self.s2) != 0:
self.s1.append(self.s2[-1])
self.s2.pop()
# Dequeue an item from the queue
def deQueue(self):
# if first stack is empty
if len(self.s1) == 0:
print("Q is Empty")
# Return top of self.s1
x = self.s1[-1]
self.s1.pop()
return x
# Driver code
if __name__ == '__main__':
q = Queue()
q.enQueue(1)
q.enQueue(2)
q.enQueue(3)
print(q.deQueue())
print(q.deQueue())
print(q.deQueue())
# This code is contributed by PranchalK
C#
// C# program to implement Queue using
// two stacks with costly enQueue()
using System;
using System.Collections;
class GFG
{
public class Queue
{
public Stack s1 = new Stack();
public Stack s2 = new Stack();
public void enQueue(int x)
{
// Move all elements from s1 to s2
while (s1.Count > 0)
{
s2.Push(s1.Pop());
//s1.Pop();
}
// Push item into s1
s1.Push(x);
// Push everything back to s1
while (s2.Count > 0)
{
s1.Push(s2.Pop());
//s2.Pop();
}
}
// Dequeue an item from the queue
public int deQueue()
{
// if first stack is empty
if (s1.Count == 0)
{
Console.WriteLine("Q is Empty");
}
// Return top of s1
int x = (int)s1.Peek();
s1.Pop();
return x;
}
};
// Driver code
public static void Main()
{
Queue q = new Queue();
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
Console.Write(q.deQueue()+" ");
Console.Write(q.deQueue()+" ");
Console.Write(q.deQueue());
}
}
// This code is contributed by
// Subhadeep Gupta
Javascript
<script>
// Javascript program to implement Queue using
// two stacks with costly enQueue()
class Queue{
constructor()
{
this.s1 = [];
this.s2 = [];
}
enQueue(x)
{
// Move all elements from s1 to s2
while (this.s1.length != 0)
{
this.s2.push(this.s1.pop());
//s1.pop();
}
// Push item into s1
this.s1.push(x);
// Push everything back to s1
while (this.s2.length != 0)
{
this.s1.push(this.s2.pop());
//s2.pop();
}
}
// Dequeue an item from the queue
deQueue()
{
// If first stack is empty
if (this.s1.length == 0)
{
document.write("Q is Empty");
}
// Return top of s1
let x = this.s1[this.s1.length - 1];
this.s1.pop();
return x;
}
}
// Driver code
let q = new Queue();
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
document.write(q.deQueue() + "<br>");
document.write(q.deQueue() + "<br>");
document.write(q.deQueue() + "<br>");
// This code is contributed by rag2127
</script>
Producción:
1 2 3
Análisis de Complejidad:
- Complejidad del tiempo:
- Operación de empuje: O(N).
En el peor de los casos, tenemos la totalidad vacía de la pila 1 en la pila 2. - Operación pop: O(1).
Igual que la operación pop en la pila.
- Operación de empuje: O(N).
- Espacio Auxiliar: O(N).
Uso de la pila para almacenar valores.
Método 2 (Al hacer que la operación de eliminación de cola sea costosa): en este método, en la operación en cola, el nuevo elemento se ingresa en la parte superior de la pila 1. En la operación de eliminación de cola, si la pila 2 está vacía, todos los elementos se mueven a la pila 2 y finalmente se devuelve la parte superior de la pila 2.
enQueue(q, x)
1) Push x to stack1 (assuming size of stacks is unlimited).
Here time complexity will be O(1)
deQueue(q)
1) If both stacks are empty then error.
2) If stack2 is empty
While stack1 is not empty, push everything from stack1 to stack2.
3) Pop the element from stack2 and return it.
Here time complexity will be O(n)
El método 2 es definitivamente mejor que el método 1.
El método 1 mueve todos los elementos dos veces en la operación enQueue, mientras que el método 2 (en la operación dequeue) mueve los elementos una vez y mueve elementos solo si stack2 está vacío. Entonces, la complejidad amortizada de la operación de dequeue se convierte en ![]()
Implementación del método 2:
C++
// CPP program to implement Queue using
// two stacks with costly deQueue()
#include <bits/stdc++.h>
using namespace std;
struct Queue {
stack<int> s1, s2;
// Enqueue an item to the queue
void enQueue(int x)
{
// Push item into the first stack
s1.push(x);
}
// Dequeue an item from the queue
int deQueue()
{
// if both stacks are empty
if (s1.empty() && s2.empty()) {
cout << "Q is empty";
exit(0);
}
// if s2 is empty, move
// elements from s1
if (s2.empty()) {
while (!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
}
// return the top item from s2
int x = s2.top();
s2.pop();
return x;
}
};
// Driver code
int main()
{
Queue q;
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
return 0;
}
C
/* C Program to implement a queue using two stacks */
#include <stdio.h>
#include <stdlib.h>
/* structure of a stack node */
struct sNode {
int data;
struct sNode* next;
};
/* Function to push an item to stack*/
void push(struct sNode** top_ref, int new_data);
/* Function to pop an item from stack*/
int pop(struct sNode** top_ref);
/* structure of queue having two stacks */
struct queue {
struct sNode* stack1;
struct sNode* stack2;
};
/* Function to enqueue an item to queue */
void enQueue(struct queue* q, int x)
{
push(&q->stack1, x);
}
/* Function to deQueue an item from queue */
int deQueue(struct queue* q)
{
int x;
/* If both stacks are empty then error */
if (q->stack1 == NULL && q->stack2 == NULL) {
printf("Q is empty");
getchar();
exit(0);
}
/* Move elements from stack1 to stack 2 only if
stack2 is empty */
if (q->stack2 == NULL) {
while (q->stack1 != NULL) {
x = pop(&q->stack1);
push(&q->stack2, x);
}
}
x = pop(&q->stack2);
return x;
}
/* Function to push an item to stack*/
void push(struct sNode** top_ref, int new_data)
{
/* allocate node */
struct sNode* new_node = (struct sNode*)malloc(sizeof(struct sNode));
if (new_node == NULL) {
printf("Stack overflow \n");
getchar();
exit(0);
}
/* put in the data */
new_node->data = new_data;
/* link the old list off the new node */
new_node->next = (*top_ref);
/* move the head to point to the new node */
(*top_ref) = new_node;
}
/* Function to pop an item from stack*/
int pop(struct sNode** top_ref)
{
int res;
struct sNode* top;
/*If stack is empty then error */
if (*top_ref == NULL) {
printf("Stack underflow \n");
getchar();
exit(0);
}
else {
top = *top_ref;
res = top->data;
*top_ref = top->next;
free(top);
return res;
}
}
/* Driver function to test anove functions */
int main()
{
/* Create a queue with items 1 2 3*/
struct queue* q = (struct queue*)malloc(sizeof(struct queue));
q->stack1 = NULL;
q->stack2 = NULL;
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
return 0;
}
Java
/* Java Program to implement a queue using two stacks */
// Note that Stack class is used for Stack implementation
import java.util.Stack;
public class GFG {
/* class of queue having two stacks */
static class Queue {
Stack<Integer> stack1;
Stack<Integer> stack2;
}
/* Function to push an item to stack*/
static void push(Stack<Integer> top_ref, int new_data)
{
// Push the data onto the stack
top_ref.push(new_data);
}
/* Function to pop an item from stack*/
static int pop(Stack<Integer> top_ref)
{
/*If stack is empty then error */
if (top_ref.isEmpty()) {
System.out.println("Stack Underflow");
System.exit(0);
}
// pop the data from the stack
return top_ref.pop();
}
// Function to enqueue an item to the queue
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
/* Function to deQueue an item from queue */
static int deQueue(Queue q)
{
int x;
/* If both stacks are empty then error */
if (q.stack1.isEmpty() && q.stack2.isEmpty()) {
System.out.println("Q is empty");
System.exit(0);
}
/* Move elements from stack1 to stack 2 only if
stack2 is empty */
if (q.stack2.isEmpty()) {
while (!q.stack1.isEmpty()) {
x = pop(q.stack1);
push(q.stack2, x);
}
}
x = pop(q.stack2);
return x;
}
/* Driver function to test above functions */
public static void main(String args[])
{
/* Create a queue with items 1 2 3*/
Queue q = new Queue();
q.stack1 = new Stack<>();
q.stack2 = new Stack<>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
System.out.print(deQueue(q) + " ");
System.out.print(deQueue(q) + " ");
System.out.println(deQueue(q) + " ");
}
}
// This code is contributed by Sumit Ghosh
Python3
# Python3 program to implement Queue using
# two stacks with costly deQueue()
class Queue:
def __init__(self):
self.s1 = []
self.s2 = []
# EnQueue item to the queue
def enQueue(self, x):
self.s1.append(x)
# DeQueue item from the queue
def deQueue(self):
# if both the stacks are empty
if len(self.s1) == 0 and len(self.s2) == 0:
print("Q is Empty")
return
# if s2 is empty and s1 has elements
elif len(self.s2) == 0 and len(self.s1) > 0:
while len(self.s1):
temp = self.s1.pop()
self.s2.append(temp)
return self.s2.pop()
else:
return self.s2.pop()
# Driver code
if __name__ == '__main__':
q = Queue()
q.enQueue(1)
q.enQueue(2)
q.enQueue(3)
print(q.deQueue())
print(q.deQueue())
print(q.deQueue())
# This code is contributed by Pratyush Kumar
C#
/* C# Program to implement a queue using two stacks */
// Note that Stack class is used for Stack implementation
using System;
using System.Collections.Generic;
class GFG
{
/* class of queue having two stacks */
public class Queue
{
public Stack<int> stack1;
public Stack<int> stack2;
}
/* Function to push an item to stack*/
static void push(Stack<int> top_ref, int new_data)
{
// Push the data onto the stack
top_ref.Push(new_data);
}
/* Function to pop an item from stack*/
static int pop(Stack<int> top_ref)
{
/*If stack is empty then error */
if (top_ref.Count == 0)
{
Console.WriteLine("Stack Underflow");
Environment.Exit(0);
}
// pop the data from the stack
return top_ref.Pop();
}
// Function to enqueue an item to the queue
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
/* Function to deQueue an item from queue */
static int deQueue(Queue q)
{
int x;
/* If both stacks are empty then error */
if (q.stack1.Count == 0 && q.stack2.Count == 0)
{
Console.WriteLine("Q is empty");
Environment.Exit(0);
}
/* Move elements from stack1 to stack 2 only if
stack2 is empty */
if (q.stack2.Count == 0)
{
while (q.stack1.Count != 0)
{
x = pop(q.stack1);
push(q.stack2, x);
}
}
x = pop(q.stack2);
return x;
}
/* Driver code */
public static void Main(String []args)
{
/* Create a queue with items 1 2 3*/
Queue q = new Queue();
q.stack1 = new Stack<int>();
q.stack2 = new Stack<int>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
Console.Write(deQueue(q) + " ");
Console.Write(deQueue(q) + " ");
Console.WriteLine(deQueue(q) + " ");
}
}
// This code is contributed by 29AjayKumar
Producción:
1 2 3
Análisis de Complejidad:
- Complejidad del tiempo:
- Operación de empuje: O(1).
Igual que la operación pop en la pila. - Operación pop: O(N).
En el peor de los casos, tenemos la totalidad vacía de la pila 1 en la pila 2
- Operación de empuje: O(1).
- Espacio Auxiliar: O(N).
Uso de la pila para almacenar valores.
La cola también se puede implementar utilizando una pila de usuario y una pila de llamadas de función. A continuación se modifica el Método 2 donde se utiliza la recursividad (o pila de llamadas de función) para implementar la cola usando solo una pila definida por el usuario.
enQueue(x)
1) Push x to stack1.
deQueue:
1) If stack1 is empty then error.
2) If stack1 has only one element then return it.
3) Recursively pop everything from the stack1, store the popped item
in a variable res, push the res back to stack1 and return res
El paso 3 se asegura de que siempre se devuelva el último elemento extraído y, dado que la recursión se detiene cuando solo hay un elemento en la pila 1 (paso 2), obtenemos el último elemento de la pila 1 en deQueue() y todos los demás elementos se vuelven a insertar. paso
3. Implementación del método 2 utilizando Function Call Stack:
C++
// CPP program to implement Queue using
// one stack and recursive call stack.
#include <bits/stdc++.h>
using namespace std;
struct Queue {
stack<int> s;
// Enqueue an item to the queue
void enQueue(int x)
{
s.push(x);
}
// Dequeue an item from the queue
int deQueue()
{
if (s.empty()) {
cout << "Q is empty";
exit(0);
}
// pop an item from the stack
int x = s.top();
s.pop();
// if stack becomes empty, return
// the popped item
if (s.empty())
return x;
// recursive call
int item = deQueue();
// push popped item back to the stack
s.push(x);
// return the result of deQueue() call
return item;
}
};
// Driver code
int main()
{
Queue q;
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
return 0;
}
C
/* Program to implement a queue using one user defined stack
and one Function Call Stack */
#include <stdio.h>
#include <stdlib.h>
/* structure of a stack node */
struct sNode {
int data;
struct sNode* next;
};
/* structure of queue having two stacks */
struct queue {
struct sNode* stack1;
};
/* Function to push an item to stack*/
void push(struct sNode** top_ref, int new_data);
/* Function to pop an item from stack*/
int pop(struct sNode** top_ref);
/* Function to enqueue an item to queue */
void enQueue(struct queue* q, int x)
{
push(&q->stack1, x);
}
/* Function to deQueue an item from queue */
int deQueue(struct queue* q)
{
int x, res;
/* If both stacks are empty then error */
if (q->stack1 == NULL) {
printf("Q is empty");
getchar();
exit(0);
}
else if (q->stack1->next == NULL) {
return pop(&q->stack1);
}
else {
/* pop an item from the stack1 */
x = pop(&q->stack1);
/* store the last deQueued item */
res = deQueue(q);
/* push everything back to stack1 */
push(&q->stack1, x);
return res;
}
}
/* Function to push an item to stack*/
void push(struct sNode** top_ref, int new_data)
{
/* allocate node */
struct sNode* new_node = (struct sNode*)malloc(sizeof(struct sNode));
if (new_node == NULL) {
printf("Stack overflow \n");
getchar();
exit(0);
}
/* put in the data */
new_node->data = new_data;
/* link the old list off the new node */
new_node->next = (*top_ref);
/* move the head to point to the new node */
(*top_ref) = new_node;
}
/* Function to pop an item from stack*/
int pop(struct sNode** top_ref)
{
int res;
struct sNode* top;
/*If stack is empty then error */
if (*top_ref == NULL) {
printf("Stack underflow \n");
getchar();
exit(0);
}
else {
top = *top_ref;
res = top->data;
*top_ref = top->next;
free(top);
return res;
}
}
/* Driver function to test above functions */
int main()
{
/* Create a queue with items 1 2 3*/
struct queue* q = (struct queue*)malloc(sizeof(struct queue));
q->stack1 = NULL;
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
return 0;
}
Java
// Java Program to implement a queue using one stack
import java.util.Stack;
public class QOneStack {
// class of queue having two stacks
static class Queue {
Stack<Integer> stack1;
}
/* Function to push an item to stack*/
static void push(Stack<Integer> top_ref, int new_data)
{
/* put in the data */
top_ref.push(new_data);
}
/* Function to pop an item from stack*/
static int pop(Stack<Integer> top_ref)
{
/*If stack is empty then error */
if (top_ref == null) {
System.out.println("Stack Underflow");
System.exit(0);
}
// return element from stack
return top_ref.pop();
}
/* Function to enqueue an item to queue */
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
/* Function to deQueue an item from queue */
static int deQueue(Queue q)
{
int x, res = 0;
/* If the stacks is empty then error */
if (q.stack1.isEmpty()) {
System.out.println("Q is Empty");
System.exit(0);
}
// Check if it is a last element of stack
else if (q.stack1.size() == 1) {
return pop(q.stack1);
}
else {
/* pop an item from the stack1 */
x = pop(q.stack1);
/* store the last deQueued item */
res = deQueue(q);
/* push everything back to stack1 */
push(q.stack1, x);
return res;
}
return 0;
}
/* Driver function to test above functions */
public static void main(String[] args)
{
/* Create a queue with items 1 2 3*/
Queue q = new Queue();
q.stack1 = new Stack<>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
System.out.print(deQueue(q) + " ");
System.out.print(deQueue(q) + " ");
System.out.print(deQueue(q) + " ");
}
}
// This code is contributed by Sumit Ghosh
Python3
# Python3 program to implement Queue using
# one stack and recursive call stack.
class Queue:
def __init__(self):
self.s = []
# Enqueue an item to the queue
def enQueue(self, data):
self.s.append(data)
# Dequeue an item from the queue
def deQueue(self):
# Return if queue is empty
if len(self.s) <= 0:
print('Queue is empty')
return
# pop an item from the stack
x = self.s[len(self.s) - 1]
self.s.pop()
# if stack become empty
# return the popped item
if len(self.s) <= 0:
return x
# recursive call
item = self.deQueue()
# push popped item back to
# the stack
self.s.append(x)
# return the result of
# deQueue() call
return item
# Driver code
if __name__ == '__main__':
q = Queue()
q.enQueue(1)
q.enQueue(2)
q.enQueue(3)
print(q.deQueue())
print(q.deQueue())
print(q.deQueue())
# This code is contributed by iArman
C#
// C# Program to implement a queue using one stack
using System;
using System.Collections.Generic;
public class QOneStack
{
// class of queue having two stacks
public class Queue
{
public Stack<int> stack1;
}
/* Function to push an item to stack*/
static void push(Stack<int> top_ref, int new_data)
{
/* put in the data */
top_ref.Push(new_data);
}
/* Function to pop an item from stack*/
static int pop(Stack<int> top_ref)
{
/*If stack is empty then error */
if (top_ref == null)
{
Console.WriteLine("Stack Underflow");
Environment.Exit(0);
}
// return element from stack
return top_ref.Pop();
}
/* Function to enqueue an item to queue */
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
/* Function to deQueue an item from queue */
static int deQueue(Queue q)
{
int x, res = 0;
/* If the stacks is empty then error */
if (q.stack1.Count == 0)
{
Console.WriteLine("Q is Empty");
Environment.Exit(0);
}
// Check if it is a last element of stack
else if (q.stack1.Count == 1)
{
return pop(q.stack1);
}
else
{
/* pop an item from the stack1 */
x = pop(q.stack1);
/* store the last deQueued item */
res = deQueue(q);
/* push everything back to stack1 */
push(q.stack1, x);
return res;
}
return 0;
}
/* Driver function to test above functions */
public static void Main(String[] args)
{
/* Create a queue with items 1 2 3*/
Queue q = new Queue();
q.stack1 = new Stack<int>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
/* Dequeue items */
Console.Write(deQueue(q) + " ");
Console.Write(deQueue(q) + " ");
Console.Write(deQueue(q) + " ");
}
}
// This code is contributed by Princi Singh
Producción:
1 2 3
Análisis de Complejidad:
- Complejidad del tiempo:
- Operación de empuje: O(1).
Igual que la operación pop en la pila. - Operación emergente: O(N).
La diferencia con el método anterior es que en este método se devuelve el elemento y todos los elementos se restauran en una sola llamada.
- Operación de empuje: O(1).
- Espacio Auxiliar: O(N).
Uso de la pila para almacenar valores.
Escriba comentarios si encuentra que alguno de los códigos/algoritmos anteriores es incorrecto o encuentra mejores formas de resolver el mismo problema.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
