Colisiones en una dimensión

Durante el juego, es posible que hayas visto dos bolas de billar chocar entre sí. La colisión es la unión violenta de dos cuerpos distintos. ¿Qué sucede cuando dos objetos chocan? ¿Podemos identificar la velocidad o la trayectoria de los cuerpos que chocan? ¡Vamos a investigar!

Una colisión ocurre cuando dos cosas entran en contacto entre sí por un breve período de tiempo. En otros términos, una colisión es un contacto recíproco a corto plazo entre dos masas en el que cambia el momento y la energía de las masas que chocan. Es posible que haya visto el efecto de un golpeador en las monedas cuando chocaron mientras jugaban carambolas.

Coeficiente de restitución

La relación entre la velocidad final y la velocidad inicial de las partículas que interactúan después de producirse una colisión entre ellas se denomina coeficiente de restitución. El coeficiente de restitución se denota por ‘e’ con un valor que va de 0 a 1. Dado que el coeficiente de restitución es una mercancía constante, no tiene ninguna dimensión. Proporciona más información sobre la elasticidad de la colisión. La colisión perfectamente elástica donde no hay pérdida de energía cinética total del sistema. Es básicamente un valor entero, que representa la medida de la naturaleza de los materiales en colisión.

El valor máximo del coeficiente de restitución es e =1.

La fórmula para el coeficiente de restitución es,

e = Velocidad relativa antes de la colisión / Velocidad relativa después de la colisión

Rango de valores para e

Dado que el coeficiente de restitución se encuentra entre el intervalo de 0 a 1, puede contener el siguiente rango de valores:

Para e = 0, se refiere a una colisión perfectamente inelástica. La energía cinética máxima se pierde durante la ocurrencia de tal tipo de colisión.
Si 0 < e < 1, se refiere a una colisión inelástica del mundo real, es decir, en este tipo de colisión, se pierde algo de energía cinética.
Si e = 1, se refiere a una colisión perfectamente elástica en la que no se disipa energía cinética. Los objetos rebotan con la misma velocidad con la que se acercan unos a otros.

Tipos de colisión

De acuerdo con la ley de conservación del momento, no hay pérdida de energía durante la colisión de objetos con masas individuales. Sin embargo, puede haber ciertas colisiones sin seguir la conservación de la energía cinética. Con base en la conservación de energía que se sigue durante las colisiones, se pueden diseñar las siguientes categorías:

(1) Colisión Elástica

Las colisiones elásticas conservan el momento total y la energía total. La energía cinética total puede o no conservarse. Dado que las fuerzas involucradas durante la colisión se conservan en la naturaleza, la forma de energía mecánica no se convierte en ninguna otra forma de energía.

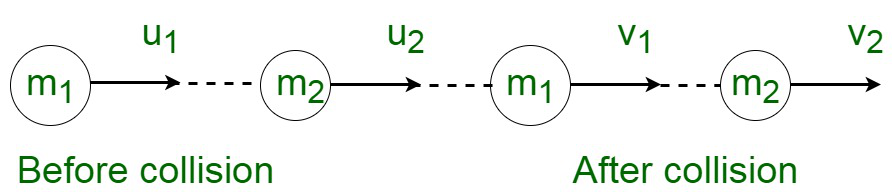
Supongamos dos objetos con masas, m ₁ y m ₂ viajando con velocidades u ₁ y u ₂ respectivamente. Sean las velocidades finales después de la colisión de estos dos objetos v ₁ y v ₂ .

De acuerdo con la ley de conservación de la cantidad de movimiento, tenemos:

metro ₁ tu ₁ + metro ₂ tu ₂ = metro ₁ v ₁ + metro ₂ v ₂

Según la conservación de la energía cinética:

$\frac{1}{2} m_1u^2_1 + \frac{1}{2} m_2u^2_2 = \frac{1}{2} m_1v^2_1 +\frac{1}{2} m_2v^2_2$

Ejemplos de Colisión Elástica son:

La colisión entre dos bolas de billar.
Lanzar y recuperar una pelota.

Las aplicaciones de Elastic Collision son:

El tiempo de colisión es inversamente proporcional a la fuerza que actúa entre los cuerpos que interactúan. Para maximizar la fuerza que actúa entre dos cuerpos, se debe reducir el tiempo de colisión. Lo mismo es posible para el otro caso. Esto implica que para minimizar la fuerza entre dos cuerpos, se debe aumentar el tiempo de colisión.

Los conceptos son visibles en el concepto de la introducción de bolsas de aire en los vehículos. La idea es proporcionar un mayor tiempo de colapso para minimizar el efecto de la fuerza sobre los objetos durante una colisión. Las bolsas de aire en los automóviles logran esto aumentando el tiempo requerido para detener el impulso tanto del pasajero como del conductor del automóvil.

(2) Colisión Inelástica

Las colisiones inelásticas conservan el momento total y la energía total. La energía cinética total puede o no conservarse. La energía se transforma en otras formas de energía, es decir, calor y luz. Los objetos que interactúan pueden pegarse entre sí o comenzar a moverse alineados en la misma dirección.

Por la ley de conservación de la cantidad de movimiento, tenemos,

Como los objetos se mueven en la misma dirección, ambos objetos se mueven con la misma velocidad, v,

metro ₁ tu ₁ + metro ₂ tu ₂ = (m ₁ + metro ₂ )v

$v= \frac{m_1u_1 + m_2u_2}{m_1 + m_2}$

La energía cinética de las masas antes del choque es: KE ₁ = $\frac{1}{2} m_1u^2_1 + \frac{1}{2} m_2u^2_2$
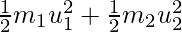
La energía cinética después de la colisión es: KE ₂ = 1/2 (m ₁ + m ₂ ) v ₂

Por la ley de conservación de la energía,

$\frac{1}{2} m_1u^2_1 + \frac{1}{2} m_2u^2_2 = \frac{1}{2} (m_1+ m_2) v_2 + Q$

donde ‘Q’ se refiere al cambio de energía que resulta en la producción de calor o sonido.

Ejemplos de Colisión Inelástica son:

Accidente de dos vehículos.
Un auto chocando contra un árbol.
La pelota cayó desde cierta altura sin poder subir a su altura original.

Colisión unidimensional

La colisión en la que las velocidades inicial y final de las masas involucradas se encuentran en una línea. Todas las variables involucradas en el movimiento ocurren en una sola dimensión.

(1) Colisión unidimensional elástica

En los choques elásticos se conservan el momento y la energía cinética interna. Dado que las colisiones elásticas se pueden simular solo con partículas microscópicas como electrones o neutrones. Considere dos protones con las masas m ₁ y m ₂

Por la ley de conservación de la cantidad de movimiento, tenemos,

metro ₁ tu ₁ + metro ₂ tu ₂ = metro ₁ v ₁ + metro ₂ v ₂

Debido a la conservación de la energía cinética,

$\frac{1}{2} m_1u^2_1 + \frac{1}{2} m_2u^2_2 = \frac{1}{2} m_1v^2_1 +\frac{1}{2} m_2v^2_2$

Esto implica,

$m_1u^2_1 + m_2u^2_2 = m_1v^2_1 + m_2v^2_2$ (Factorizando 1/2)

Reordenando obtenemos: $m_1u^2_1- m_1v^2_1 = m_2v^2_2 - m_2u^2_2$

Por lo tanto,

$m_1(u^2_1- v^2_1)= m_2(v^2_2 - u^2_2)$

En la expansión, se convierte en,

$m_1(u_1+v_1 ) (u_1- v_1 )=m_2 (v_2 + u_2)(v_2 - u_2)$

Por la conservación de la cantidad de movimiento:

$m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2$

Agrupándolo usando las mismas masas:

$m_1u_1-m_1v_1 = m_2v_2 -m_2u_2$

Por lo tanto,

$m_1(u_1-v_1) = m_2(v_2 -u_2)$

Al dividir las dos ecuaciones:

$m_1(u_1+v_1) (u_1- v_1) = \frac{m_2 (v_2 + u_2)(v_2 - u_2) }{ m_1(u_1-v_1 )} = m_2(v_2 -u_2 )$

implicamos,

$u_1+v_1 = v_2 + u_2$

Ahora,

$v_1 = v_2 + u_2- u_1$

Sustituyendo el valor de $v_1$

$v_2 = \frac{[2 m_1 u_1 + u_2 (m_2-m_1)] }{ (m_1 + m_2 )}$ …….(1)

Ahora usando el valor de v2 en la ecuación $v_1 = v_2 + u_2- u_1$

$v_1 = \frac{[2 m_1 u_1 + u_2 (m_2-m_1)] }{ (m_1 + m_2)} + u_2- u_1\\ v_1 = \frac{[2 m_1 u_1 + u_2 (m_2-m_1) + u_2 (m_1 + m_2 ) - u_1(m_1 + m_2 )] }{ (m_1 + m_2 ) }$ …….(2)

Por reducción, obtenemos,

$v_1 = \frac{[2m_2 u_2 + u_1 ( m_1 - m_2)] }{ (m_1 +m_2 )}$

La mayor parte del tiempo después de la colisión, estas masas intercambian sus velocidades. Cuando las masas de ambos cuerpos son iguales,

$v_1 = u_2\ and\ v_2 = u_1$

En caso de que el segundo objeto de masa esté en reposo y el primer objeto de masa colisione con él, después de ocurrir una colisión, hay un intercambio en las velocidades, la primera masa se detiene y la segunda masa se mueve con la misma velocidad. a la primera misa.

Por lo tanto, $v_1$ = 0 y $v_2$ = $u_1$ . En caso de que $m_1 < m_2$ entonces, $v_1 = -u_1\ and\ v_2 = 0$

Esto implica que el cuerpo más ligero (el cuerpo con menor masa) tenderá a bombardear con su propia velocidad, mientras que la masa más pesada permanecerá estática en su posición.

Además, tenemos, por si acaso,

$m_1 > m_2\ then\ v_1 = u_1\ and\ v_2 = 2u_1$

Algunos casos especiales son:

Caso I:

En el caso de objetos de igual masa, es decir, $m_1 = m_2$

Usando la ecuación (1) y (2), tenemos,

$v_2=u_1, v_1=u_2$ .

Por lo tanto, podemos concluir que si dos cuerpos de igual masa sufren un choque elástico frontal, entonces hay un intercambio de velocidad entre las partículas. Además, el intercambio de cantidad de movimiento entre dos partículas es máximo, en este escenario.

Caso II:

Considere que la partícula objetivo está en reposo i, e $u_2=0$

Usando la ecuación (1) y (2), tenemos,

$v_2=\left(\frac{2m}{m_1+m_2}\right)u_1$ …..(3)

$v_1=\left(\frac{m_1-m_2}{m_1+m_2}\right)u_2$ ……(4)

La magnitud de KE transformada está dada por,

$\frac{\frac{1}{2}m_2v^2_2}{\frac{1}{2}m_1u^2_1}=\frac{\frac{1}{2}m_2\left(\frac{2m_1u_1}{m_1+m_2}\right)^2}{\frac{1}{2}m_1u^2_1}\\$

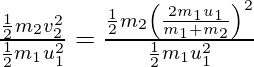
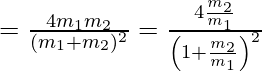$=\frac{4m_1m_2}{(m_1+m_2)^2}=\frac{4\frac{m_2}{m_1}}{\left(1+\frac{m_2}{m_1}\right)^2}$ ……(5)

cuando $m_1=m_2$ , entonces en esta condición $v_0=0\ and\ v_2=u_1$

y parte de la KE transferida sería

Por lo tanto, después de la colisión, los respectivos estados y velocidades de las partículas se intercambian, la primera partícula se detiene y la segunda partícula comienza a moverse con la velocidad de la primera partícula.

En este escenario, donde $m_1=m_2$ la transferencia de energía es total, eso es del 100%.

Y, en caso $m_1 > m_2$ o $m_1 < m_2$ , entonces la transformación de energía no es equivalente al 100%.

Caso III:

Si $m_2 >>>> m_1\ and\ u_2=0$

Usando la ecuación (3) y (4), tenemos,

$v_1 ≅ -u_1\ and\ v_2=0$ ……..(6)

Caso IV:

Si $m_1 >>>> m_2\ and\ u_2=0$

Usando la ecuación (3) y (4), tenemos,

$v_1 ≅ u_1\ and\ v_2=2u_1$ ………(7)

Por lo tanto,

Podemos concluir que cuando una partícula con una masa mayor choca con una partícula de masa insignificantemente más liviana en reposo, luego de la colisión, la partícula pesada mantiene la misma velocidad y la partícula liviana comienza a moverse con una velocidad doble que la de una partícula más pesada. objeto de masa.

(2) Colisión unidimensional inelástica

El momento de las partículas involucradas permanece conservado, por lo que la energía cinética cambia a diferentes formas de energía.

Por la ley de conservación de la cantidad de movimiento, tenemos,

$m_1u_1 + m_2u_2 = (m_1 + m_2) v$

Dado que en una colisión unidimensional inelástica, ambos objetos tienden a moverse con la misma velocidad v, tenemos,

$v = m_1u_1 + \frac{m_2u_2}{ m_1 + m_2}$

La pérdida de energía cinética se puede igualar a:

$E = \frac{1}{2} m_1u^2_2 - \frac{1}{2} (m_1 + m_2) v_2$

Problema de muestra

Problema 1. Un objeto con masa m que se mueve con velocidad V m/s sufre una colisión con otro cuerpo con el doble de su propia masa originalmente en reposo. Calcule la razón de KE antes y después de la colisión.

Solución:

Masa del primer objeto = m

Masa del segundo objeto = 2m

La relación de KE antes y después de la colisión será de 9:1.

Problema 2: Calcular el coeficiente de restitución cuando una pelota de goma cae del techo situado a una altura de 10 m. Rebota dos veces y alcanza una altura final de 2,5 m.

Solución:

El coeficiente de restitución está dado por,

$e=\frac{Relative\ speed\ after\ collision}{Relative\ speed\ before\ collision}$

Al calcular, obtenemos,

$e =\frac{ 1}{\sqrt2}$

Problema 3: Considere dos partículas perfectamente elásticas A y B de igual masa, m con velocidades iniciales de 15 m/seg y 10 m/seg respectivamente. ¿Cuáles serán sus velocidades finales?

Solución:

Las velocidades de los cuerpos se intercambiarán después del choque, por lo tanto, las velocidades finales de las masas serán,

A B

10 15

Problema 4. Considere un cuerpo inicialmente en posición de reposo. Acelera constantemente en un movimiento unidimensional. Explique la relación entre la potencia disipada y el tiempo.

Solución:

Por la segunda ley del movimiento,

v = tu + en

v = 0 + en = en

Como sabemos que la potencia es equivalente a ,

PAG = F × v

Por lo tanto, tenemos,

PAGS = (ma) × en = ma ² t

Como m y n son constantes,

Por lo tanto, la potencia es directamente proporcional al tiempo.

P ∝ t.

Problema 5: Considere un cuerpo inicialmente en posición de reposo. Acelera constantemente en movimiento unidimensional con potencia constante. Explicar la relación entre el desplazamiento y el tiempo.

Solución:

Ya que, sabemos,

p = fuerza × velocidad

[p] = [F] [v] = [MLT ^-2 ][LT ^-1 ]

[p] = [ML ² T ^-3 ]

L ² T ^-3 = constante

⇒ $\frac{L^2}{T^2}$ = constante

L ² ∝ T ³

⇒ L ∝ $T^{\frac{3}{2}}$

Publicación traducida automáticamente

Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Coeficiente de restitución

Tipos de colisión

Colisión unidimensional

Problema de muestra

Deja una respuesta Cancelar la respuesta