En la teoría de gráficos matemáticos, un gráfico cordal es un bucle cerrado que tiene 4 o más vértices, de modo que se puede dibujar un borde desde un vértice hasta otro vértice presente en él. En otras palabras, un gráfico cordal es un gráfico de longitud 4 o más que contiene al menos una cuerda. Una cuerda no es más que un borde que conecta dos vértices del gráfico y se dibuja dentro del gráfico.
Puntos importantes para recordar:
- Un gráfico cordal es un subconjunto del gráfico completo.
- Un grafo que no contiene cuerdas se llama hueco o ciclo sin cuerdas.
- Un grafo completo es un grafo cordal en sí mismo.
1) Considere el siguiente gráfico ABCD c. Se dibuja una arista CB desde el vértice C hasta el vértice B, que actúa como cuerda en este gráfico. Por lo tanto, se dice que el siguiente gráfico es un gráfico cordal.

Gráfico de cuerdas
2) Considere el siguiente ejemplo del gráfico completo. Un grafo que consta de n*(n-1)/2 aristas se dice que es un grafo completo, donde n es el número de vértices. En el grafo completo, las aristas que conectan todos los vértices ya están presentes y también actúan como cuerda. Por lo tanto, un grafo completo es un superconjunto de un grafo cordal.

Gráfico completo
Algoritmo de coloración mínima:
En este artículo, discutiremos la coloración de los gráficos cordales usando el algoritmo de coloración codicioso .
Algoritmo de coloración codicioso:
- Primero, necesitamos encontrar el orden de eliminación perfecto (PEO) del gráfico cordal dado.
- Luego, recorre los vértices en el orden inverso de ese PEO que ya hemos encontrado.
- Da el color más pequeño a cada vértice, de modo que el color del vértice actual no se usa en los vértices vecinos.
- Si el color del vértice actual ya se le da a su vecino, incremente el color y asígnelo al vértice actual.
- Repita los pasos 3 y 4 hasta que todos los vértices estén coloreados.
Ejemplo: Considere el siguiente gráfico cordal ABCD. Sea el orden de eliminación perfecto de este gráfico [D, C, B, A]. Recorreremos el gráfico PEO en sentido inverso. Por lo tanto, [A, B, C, D] es el reverso de PEO.
1. Primero, colorearemos el vértice A con 1 ya que necesitamos colorear con el color presente más pequeño.
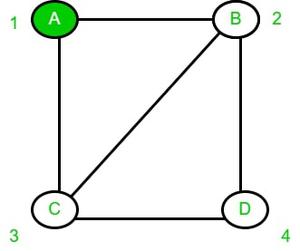
2. Ahora, para el vértice B, comprobaremos si sus vecinos contienen el color 1 o no. Como el vértice ‘A’ contiene el color 1, incrementaremos el color en 1 para colorear el vértice B.
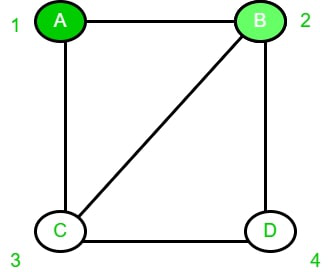
3. De manera similar, para el vértice C, su vecino A contiene el color 1 y B contiene el color 2, por lo que colorearemos el vértice C en 3.
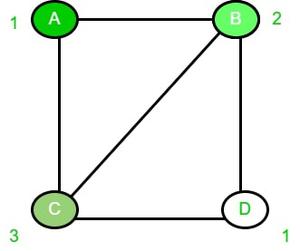
4. Ahora, para el vértice D, como sus vecinos no contienen el color 1, colorearemos 1 en el vértice D.
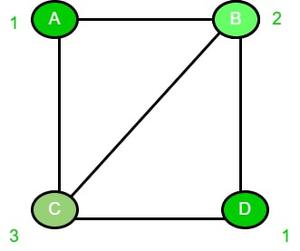
Publicación traducida automáticamente
Artículo escrito por suyashkhare9698 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA