Cómo calcular la covarianza en MATLAB

La covarianza es la medida de la fuerza de la correlación entre dos o más variables aleatorias. La covarianza de dos variables aleatorias X e Y se puede definir como:

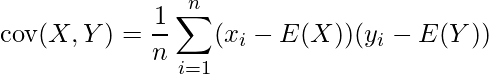
Donde E(X) y E(Y) son la expectativa o la media de las variables aleatorias X e Y respectivamente.

La array de covarianza de dos variables aleatorias A y B se define como

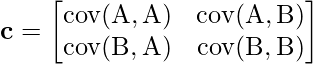
El lenguaje MATLAB permite a los usuarios calcular la covarianza de variables aleatorias utilizando el método cov(). Las diferentes sintaxis del método cov() son:

1. C = cov(A)
2. C = cov(A,B)
3. C = cov(___,w)
4. C = cov(___,bandera nan)

C = cov(A)

• Devuelve la covarianza de la array A.
• Si A es un escalar, entonces devuelve 0.
• Si A es un vector, devuelve la varianza del vector A.

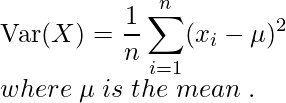
• Si A es una array, entonces considera cada columna como una variable aleatoria y devuelve la array de covarianza de la array A.

Nota: disp (x) muestra el valor de la variable X sin imprimir el nombre de la variable. Otra forma de mostrar una variable es escribir su nombre, que muestra una «X =» inicial antes del valor. Si una variable contiene una array vacía, disp regresa sin mostrar nada.

Ejemplo 1:

% Input vector
A = [1 3 4];
disp("Vector :");
disp(A);
 
% Variance of vector A
C = cov(A);
disp("Variance :");
disp(C);

Producción :

Ejemplo 2:

% Input vector
A = [2 7 1;
     3 5 1
     4 1 2];
disp("Matrix :");
disp(A);
 
% Covariance of matrix A
C = cov(A);
disp("Covariance matrix :");
disp(C);

Producción :

C = cov(A,B)

• Devuelve la array de covarianza de los arreglos A y B.
• Si A y B son vectores, entonces devuelve la array de covarianza de A y B.
• Si A y B son arrays, entonces las considera como vectores al expandir las dimensiones y devuelve la array de covarianza.

Ejemplo:

% Input vector
A = [3 5 7];
B = [-1 3 9];
disp("Vector A:");
disp(A);
disp("Vector B:");
disp(B);
 
% Covariance of vectors A,B
C = cov(A,B);
disp("Covariance matrix :");
disp(C);

Producción :

C = cov(___,w)

• Devuelve la covarianza de la array de entrada normalizándola a w.
• Si w = 1 , entonces la covarianza se normaliza por el número de filas en la array de entrada .
• Si w = 0 , entonces la covarianza se normaliza por el número de filas en la array de entrada – 1 .

Ejemplo:

% Input vector
A = [2 4 6;
     3 5 7
     8 10 12];
disp("Matrix :");
disp(A);
 
% Variance of matrix A
C = cov(A,1);
disp("Variance matrix:");
disp(C);

Producción :

C = cov(___,bandera nan)

• Devuelve la covarianza de la array de entrada considerando el nanflag.
• Si nanflag = ‘includenan’, entonces considera los valores de NaN en la array.
• Si nanflag = ‘omitrows’, omite las filas con al menos un valor NaN en la array.

Ejemplo:

% Input vector
A = [3.2 -1.005 2.98;
     NaN  -6.75  NaN;
     5.37  0.19  1]
disp("Matrix :");
disp(A);
 
% Variance of matrix A
C = cov(A,'includenan');
disp("Variance matrix including NaN:");
disp(C);
 
 
% Variance of matrix A
C = cov(A,'omitrows');
disp("Variance matrix omitting NaN:");
disp(C);

Producción :