Definición: La desviación estándar relacionada también se conoce como la forma de desviación estándar de porcentaje relativo, la medida de desviación que nos dice cómo se dispersan los diferentes números alrededor de la media en un conjunto particular de datos. Este formato muestra la distribución porcentual de los datos.
Si una desviación estándar relativa del producto es más alta, eso significa que los números están muy alejados de la media de ese producto. El equipo de RSD a veces necesita ciertos datos que están muy alejados del promedio de RSD según los requisitos del producto. Los datos que se desvían mucho de la RSD se tienen en cuenta en esos casos.
En el caso de la situación inversa, es decir, un incumplimiento relativo más bajo, los números están más cerca que el promedio y también se denominan coeficiente de diferencia. En general, la idea de los pronósticos reales se da dentro del conjunto de datos dado.
Usos de la desviación estándar relativa:
- La desviación estándar relativa se usa ampliamente en la interpretación de las relaciones de datos estadísticos en diferentes segmentos.
- Esta es una de las principales herramientas que indican si el precio de las acciones está cambiando el crecimiento de la empresa.
- RSD es una versión sofisticada de una herramienta analítica que ayuda al usuario final a comprender las tendencias, la demanda de productos y las preferencias de los clientes en diversas industrias. RSD, por lo tanto, ayuda a detectar los resultados reales de varias opciones.
Fórmula:
RSD (desviación estándar relativa) = s × 100 / x¯
dónde,
RSD = Desviación estándar relativa
s = Desviación estándar
x¯ = Media de los datos.
Ejemplo 1: Calcula RSD cuando los números: 8,20,40,60 y la desviación estándar es 5.
Primero calculando la media (x)
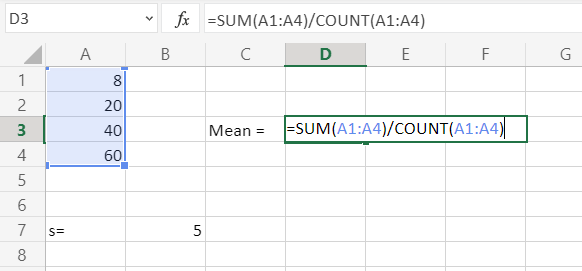
Luego calculando RSD
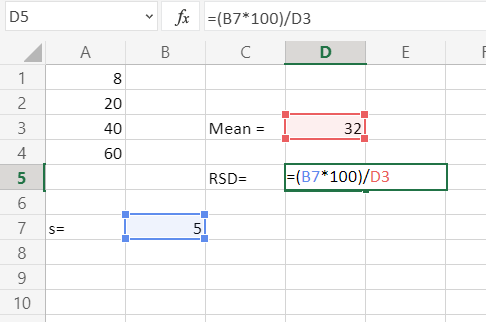
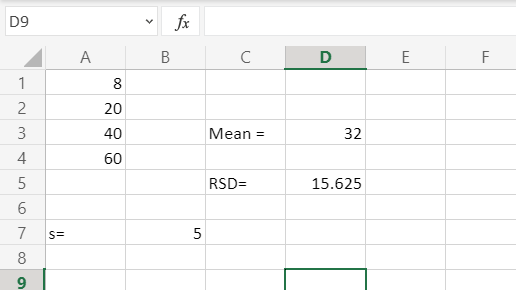
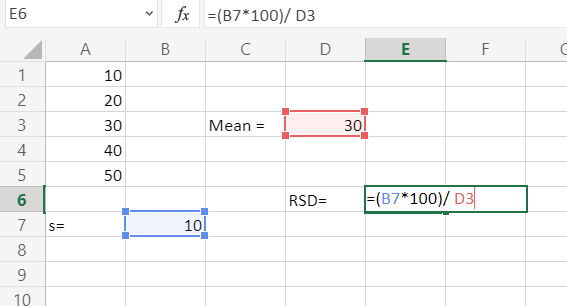
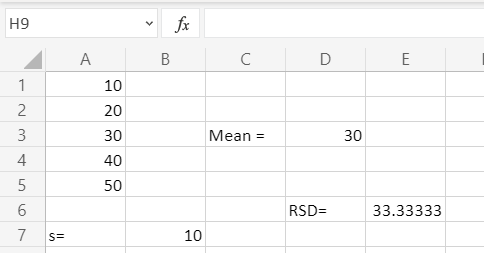
Ejemplo 2: Calcula RSD cuando los números: 10,20,30,40,50 y la desviación estándar es 10.
Primero calculando la media (x)
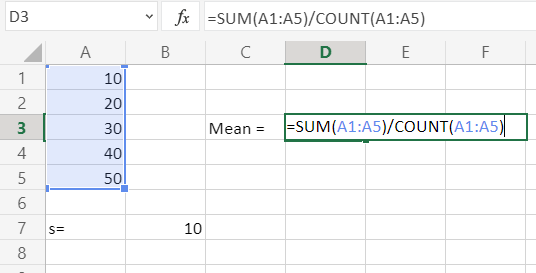
Luego calculando RSD
Publicación traducida automáticamente
Artículo escrito por priyavermaa1198 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA