Cómo crear un gráfico residual en Python

Una gráfica de residuos es un gráfico en el que los residuos se muestran en el eje y y la variable independiente se muestra en el eje x. Un modelo de regresión lineal es apropiado para los datos si los puntos en una gráfica de residuos se distribuyen aleatoriamente a lo largo del eje horizontal. Veamos cómo crear un gráfico residual en Python.

Método 1: Usar plot_regress_exog()

plot_regress_exog():

• Compare los resultados de la regresión con un regresor.
• ‘endog frente a exog’, ‘residuales frente a exog’, ‘ajustado frente a exog’ y ‘ajustado más residual frente a exog’ se trazan en una figura de 2 por 2.

Sintaxis: statsmodels.graphics.regressionplots.plot_regress_exog(resultados, exog_idx, fig=Ninguno)

Parámetros:

• resultados: instancia de resultado
• exog_idx: índice o nombre del regresor
• fig : se crea una figura si no se proporciona ninguna figura

Devoluciones: figura 2X2

Regresión lineal simple

Después de importar los paquetes necesarios y leer el archivo CSV, usamos ols() de statsmodels.formula.api para ajustar los datos a la regresión lineal. creamos una figura y pasamos esa figura, el nombre de la variable independiente y el modelo de regresión al método plot_regress_exog(). se muestra una figura 2X2 de parcelas residuales. En el método ols() la string antes de ‘~’ es la variable dependiente o la variable que estamos tratando de predecir y después de ‘~’ vienen las variables independientes. para la regresión lineal, hay una variable dependiente y una variable independiente.

ols(‘variable_respuesta ~ variable_predictor’, datos= datos)

CSV utilizado: headbrain3

# import packages and libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols
  
# reading the csv file
data = pd.read_csv('headbrain3.csv')
  
# fit simple linear regression model
linear_model = ols('Brain_weight ~ Head_size',
                   data=data).fit()
  
# display model summary
print(linear_model.summary())
  
# modify figure size
fig = plt.figure(figsize=(14, 8))
  
# creating regression plots
fig = sm.graphics.plot_regress_exog(linear_model,
                                    'Head_size',
                                    fig=fig)

Producción:

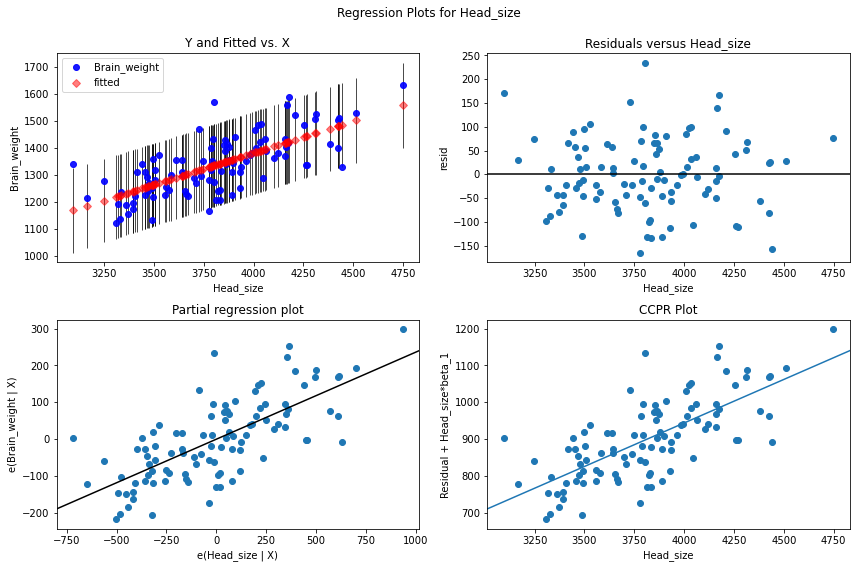
Podemos ver que los puntos se trazan aleatoriamente dispersos o dispersos. los puntos o residuos están dispersos alrededor de la línea ‘0’, no hay un patrón y los puntos no se basan en un lado, por lo que no hay problema de heteroscedasticidad. con la variable predictora ‘Head_size’ no hay heterocedasticidad. 

Regresión lineal múltiple:

En la regresión lineal múltiple, tenemos más de variables independientes o variables predictoras y una variable dependiente. El código es similar a la regresión lineal excepto que tenemos que hacer este cambio en el método ols().

ols(‘variable_respuesta ~ variable_predictor1+ variable_predictor2 +…. ‘, datos= datos)

‘+’ se usa para agregar cuántas predictor_variables queremos al crear el modelo. 

CSV Usado: precios de viviendas

Ejemplo 1:

# import packages and libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols
  
# reading the csv file
data = pd.read_csv('homeprices.csv')
data
  
# fit multi linear regression model
multi_model = ols('price ~ area + bedrooms', data=data).fit()
  
# display model summary
print(multi_model.summary())
  
# modify figure size
fig = plt.figure(figsize=(14, 8))
  
# creating regression plots
fig = sm.graphics.plot_regress_exog(multi_model, 'area', fig=fig)

Producción:

Podemos ver que los puntos se trazan aleatoriamente dispersos o dispersos. los puntos o residuos están dispersos alrededor de la línea ‘0’, no hay un patrón y los puntos no se basan en un lado, por lo que no hay problema de heteroscedasticidad. Con la variable predictora ‘área’ no hay heterocedasticidad. 

Ejemplo 2:

# import packages and libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols
  
# reading the csv file
data = pd.read_csv('homeprices.csv')
data
  
# fit multi linear regression model
multi_model = ols('price ~ area + bedrooms', data=data).fit()
  
# modify figure size
fig = plt.figure(figsize=(14, 8))
  
# creating regression plots
fig = sm.graphics.plot_regress_exog(multi_model, 'bedrooms', fig=fig)

Producción:

 podemos ver que los puntos se trazan aleatoriamente dispersos o dispersos. los puntos o residuos están dispersos alrededor de la línea ‘0’, no hay patrón y los puntos no se basan en un lado, por lo que no hay problema de heteroscedasticidad. con la variable predictora ‘dormitorios’ no hay heterocedasticidad. 

Método 2: Usar seaborn.residplot()

seaborn.residplot(): esta función retrocederá y en x y luego trazará los residuos como un diagrama de dispersión. Puede ajustar un suavizador lowess a la gráfica residual como una opción, lo que puede ayudar a detectar si los residuales tienen estructura.

Sintaxis: seaborn.residplot(*, x=Ninguno, y=Ninguno, data=Ninguno, lowess=False, x_partial=Ninguno, y_partial=Ninguno, order=1, robusto=False, dropna=True, label=Ninguno, color= Ninguno, scatter_kws=Ninguno, line_kws=Ninguno, ax=Ninguno)

Parámetros:

• x : nombre de columna de la variable independiente (predictor) o un vector.
• y: nombre de la columna de la variable dependiente (respuesta) o un vector.
• datos: parámetro opcional. marco de datos
• lowess: por defecto es falso.

A continuación se muestra un ejemplo de una gráfica de residuos simple donde x (variable independiente) es head_size del conjunto de datos e y (variable dependiente) es la columna brain_weight del conjunto de datos.

# import packages and libraries
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
  
# reading the csv file
data = pd.read_csv('headbrain3.csv')
  
sns.residplot(x='Head_size', y='Brain_weight', data=data)
  
plt.show()

Producción:  

Podemos ver que los puntos se trazan en una distribución aleatoria, no hay un patrón y los puntos no se basan en un lado, por lo que no hay problema de heteroscedasticidad.