En matemáticas, una array es un conjunto de números o símbolos en forma de rectángulo o cuadrado agrupados en filas y columnas para representar un objeto matemático o una de sus cualidades. Por ejemplo, 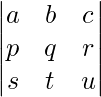 es una array cuadrada. Por otro lado,
es una array cuadrada. Por otro lado, 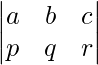 es una array rectangular.
es una array rectangular.
Determinante de una array
El determinante de la array es el producto de los componentes de cualquier fila o columna y sus respectivos cofactores. Sólo existen para arrays cuadradas, es decir, las que tienen igual número de filas y columnas. El determinante de cualquier array cuadrada A está representado por detA (o) |A|. A veces se representa por el signo. Calcular los determinantes de arrays de 1 × 1 y 2 × 2 es muy sencillo, pero el procedimiento se vuelve más complicado a medida que crece el rango de la array. Los menores y los cofactores están involucrados en el proceso de determinación del determinante de una array.
Propiedades del Determinante
- El determinante de una array y su propia transpuesta son siempre iguales, es decir,
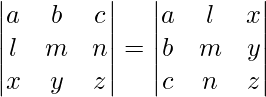
- Intercambiar dos filas o columnas cualesquiera de una array cambiaría el signo de su determinante, es decir,
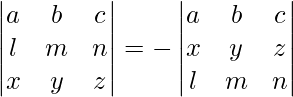 .
. - El determinante de una array con dos filas o columnas idénticas cualesquiera es cero, es decir,
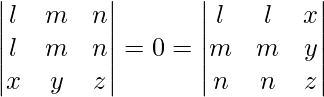 .
. - El determinante de una array con ceros como elementos de cualquiera de sus filas o columnas es cero, es decir,
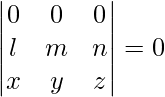
- Multiplicar cada fila de un determinante con una constante m también aumentaría el valor del determinante m veces, es decir,
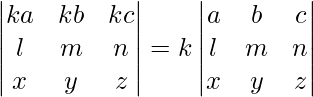 .
.
- Determinante de la array 1 × 1
Una array de 1 × 1 es una fila con solo una fila y una columna y, por lo tanto, solo un elemento. El determinante de toda array 1 × 1 siempre es igual al elemento de la array.
Ejemplo: Si la array A = [69] 1 × 1 , entonces det A o |A| = 69.
- Determinante de una array de 2 × 2
Dada la array A =
entonces su determinante viene dado por ad – bc. Simplemente se calcula multiplicando en cruz los componentes de arriba a la izquierda a abajo a la derecha y luego encontrando la diferencia de los dos.
Ejemplo: Evaluar,
Aquí, a = 4, b = 7, c = 5 y d = 8.
Por lo tanto, |A| = 4(8) – 5(7)
|A| = −3
- Determinante de una array de 3 × 3
Para encontrar el determinante de arrays de 3 × 3, necesitamos entender el término menor de un elemento,
Menor de un elemento
El determinante de una array cuadrada de cualquier orden derivada de la eliminación de la fila y la columna que contiene el elemento es el menor del elemento.
Ejemplo: Encuentra el menor de 6 en la array ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right].](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b818b7e941bed8fb634807db2058332d_l3.png)
Solución:
Dado que 6 se encuentra en la segunda fila y la tercera columna de la array dada, su array sería igual al determinante de la array obtenida al eliminar la segunda fila y la tercera columna.
Menor de 6 =
= 8 × 1 – 2 × 7
= 8 – 14
= -6
Se deben seguir los siguientes pasos,
- Seleccione cualquier fila o columna. Para encontrar el determinante, normalmente comenzamos con la primera fila.
- Determine los cofactores de cada uno de los elementos de fila/columna que elegimos en el Paso 1.
- Multiplique los elementos de la fila/columna del Paso 1 por los cofactores apropiados del Paso 2.
- Sume todos los productos del Paso 3 para obtener el determinante de la array.
Alternativamente, la siguiente fórmula también se puede utilizar para este propósito:
|A| = a(ei − fh) − b(di − fg) + c(dh − ej)
Problemas de muestra
Pregunta 1. Encuentra el menor de 9 en la array ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-35455b609cb90690101c2884b3589e1e_l3.png) .
.
Solución:
Dado que 9 se encuentra en la tercera fila y la tercera columna de la array dada, su array sería igual al determinante de la array obtenida al eliminar la tercera fila y la tercera columna.
Menor de 9 =
= 1 × 5 – 2 × 4
= 5 – 8
= -3
Pregunta 2. Encuentra el valor de |4A| si A = ![Rendered by QuickLaTeX.com \left[\begin{array}{lll}1 & 1 & -1\\1 & 2 & 2\\0 & 3 & 4\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8281d1ead447b72e779416a516f0233_l3.png) .
.
Solución:
un =
Así, 4A =
Ahora, |4A| = 4 (128 – 96) – 4 (64 – 0) – 4 (48 – 0)
= 4(32) – 4(64) – 4(48)
|4A| = -320
Pregunta 3: Encuentra x si el determinante de la array ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}4&8\\2 & x\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d74115a4d342dd000073ddda2c3a4b79_l3.png) es 0.
es 0.
Solución:
Dado: A =
|A| = 4(x) – 8(2)
= 4x – 16
Desde |A| = 0.
⇒ 4x – 16 = 0
o, 4x = 16
⇒ x = 4
Pregunta 4: Evaluar: ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}2&8&5&-3\\0&1&3&4\\6&24&15&-9\\7&2&1&10\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-47f8488efe364530fff999eb89857f29_l3.png) . Utilizar las propiedades de los determinantes.
. Utilizar las propiedades de los determinantes.
Solución:
Claramente, los elementos de la tercera fila tienen 3 como factor común. Se puede representar como:
Dado que la primera y la tercera fila de la array dada ahora son iguales, usando la tercera propiedad, el valor de la array sería cero.
|A| = 3 × 0
|A| = 0
Pregunta 5: Encuentra el valor de (a 2 + b 2 – c 2 )|A| si A = 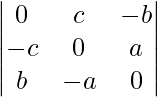 .
.
Solución:
|A| = 0(0(0) – a(a)) – c(0(-c) – a(b)) + (-b)((-c)(-a) – 0(b))
= 0 × (a 2 ) − c(0 − ab) − b(ac – 0)
= 0
Por lo tanto, (a 2 + b 2 – c 2 )|A| = (a 2 + b 2 – c 2 )(0)
⇒ (a 2 + b 2 – c 2 )|A| = 0
Pregunta 6: Encuentra t si el determinante de la array ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}0&x\\5&3\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-552c545ae73b6447f861cde71119d51d_l3.png) es 10.
es 10.
Solución:
Dado: A =
|A| = 3(0) – 5(x)
= 0 – 5x
= -5x
Desde |A| = 10.
⇒ -5x = 10
⇒ x = -2
Pregunta 7: Encuentra x si el determinante de la array ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}5&1\\3&x\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e19576b86555ef52e4d08bafc84334c3_l3.png) es 12.
es 12.
Solución:
Dado: A =
|A| = 5(x) – 3(1)
= 5x – 3
Desde |A| = 12
⇒ 5x – 3 = 12
⇒ 5x = 15
⇒ x = 3
Pregunta 8: Evaluar: 
Solución:
Aquí, a = 1, b = 2, c = 3, d = 4, e = 5, f = 6, g = 7, h = 8, i = 9.
Así, |A| = 1(5(9) – 6(8)) – 2(4(9) – 6(7)) + 3(4(8) – 5(7))
= 1(45 – 42) – 2(36 – 42) + 3(32 – 35)
= 1(3) – 2(-6) + 3(-3)
= 3 + 12 – 9
⇒ |A| = 0
Publicación traducida automáticamente
Artículo escrito por kamaljeet69420 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
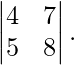


![Rendered by QuickLaTeX.com \left[\begin{array}{lll}1 & 1 & -1\\1 & 2 & 2\\0 & 3 & 4\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4346f614db9e4ddacbc17dd8adec2c6e_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{lll}4 & 4 & -4\\4 & 8 & 8\\0 & 12 & 16\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a206b93af464009524c5811c3ea84407_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{cc}4&8\\2 & x\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b9e05634d010bfcb6b0b8429e6d3a88e_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{cc}2&8&5&-3\\0&1&3&4\\6&24&15&-9\\7&2&1&10\end{array}\right]=3\left[\begin{array}{cc}2&8&5&-3\\0&1&3&4\\2&8&5&-3\\7&2&1&10\end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-30796bfb2cad3c1385221177a8d3b7fb_l3.png)