En este artículo, discutiremos cómo encontrar la desviación estándar en el lenguaje de programación R. La desviación estándar es la medida de la dispersión de los valores. También se puede definir como la raíz cuadrada de la varianza.
Fórmula de la desviación estándar de la muestra:
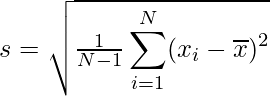
dónde,
- s = desviación estándar de la muestra
- N = Número de entidades
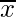= Media de entidades
Básicamente, hay dos formas diferentes de calcular la desviación estándar en el lenguaje de programación R, ambas se analizan a continuación.
Método 1: enfoque ingenuo
En este método de cálculo de la desviación estándar, utilizaremos la fórmula estándar anterior de la desviación estándar de la muestra en lenguaje R.
Ejemplo 1:
R
v <- c(12,24,74,32,14,29,84,56,67,41) s<-sqrt(sum((v-mean(v))^2/(length(v)-1))) print(s)
Producción:
[1] 25.53886
Ejemplo 2:
R
v <- c(1.8,3.7,9.2,4.7,6.1,2.8,6.1,2.2,1.4,7.9) s<-sqrt(sum((v-mean(v))^2/(length(v)-1))) print(s)
Producción:
[1] 2.676004
Método 2: Usar sd()
La función sd() se usa para devolver la desviación estándar.
Sintaxis: sd(x, na.rm = FALSO)
Parámetros:
- x: un vector numérico, array o marco de datos.
- na.rm: ¿se eliminarán los valores faltantes?
Devuelve: La desviación estándar muestral de x.
Ejemplo 1:
R
v <- c(12,24,74,32,14,29,84,56,67,41) s<-sd(v) print(s)
Producción:
[1] 25.53886
Ejemplo 2:
R
v <- c(71,48,98,65,45,27,39,61,50,24,17) s1<-sqrt(sum((v-mean(v))^2/(length(v)-1))) print(s1) s2<-sd(v) print(s2)
Producción:
[1] 23.52175
Ejemplo 3:
R
v <- c(1.8,3.7,9.2,4.7,6.1,2.8,6.1,2.2,1.4,7.9) s1<-sqrt(sum((v-mean(v))^2/(length(v)-1))) print(s1) s2<-sd(v) print(s2)
Producción:
[1] 2.676004