Cómo identificar si una lengua es regular o no

Prerrequisito: expresiones regulares, gramática regular y lenguajes regulares , lema de bombeo 
Existe un teorema bien establecido para identificar si un idioma es regular o no, basado en el principio del casillero, llamado lema de bombeo . Pero el lema de bombeo es una prueba de negatividad, es decir, si un idioma no satisface el lema de bombeo, definitivamente podemos decir que no es regular, pero si lo satisface, entonces el idioma puede ser regular o no. Pumping Lemma es más una prueba matemática, toma más tiempo y puede ser confuso a veces. En los exámenes, debemos abordar este problema muy rápidamente, por lo que, en base a observaciones y análisis comunes, aquí hay algunas reglas rápidas que ayudarán: 

1. Todo conjunto finito representa un lenguaje regular. 
   Ejemplo 1: todas las strings de longitud = 2 sobre {a, b}*, es decir, L = {aa, ab, ba, bb} es regular. 

    

2. Dada una expresión de lenguaje no regular, pero el valor del parámetro está limitado por alguna constante, entonces el lenguaje es regular (significa que tiene una especie de comparación finita). 
   Ejemplo 2 – L = { [Tex]b^n [/Tex]| n <= 10 ¹⁰¹⁰ } es regular, porque tiene un límite superior y, por lo tanto, es un lenguaje finito. 

    

3. El patrón de strings que forman un AP (progresión aritmética) es regular (es decir, su poder está en forma de expresión lineal), 
   pero el patrón con GP (progresión geométrica) no es regular (es decir, su poder está en forma de expresión no lineal) y viene bajo la clase de Lenguaje Sensible al Contexto. 
   Ejemplo 3 – L = {  | n>=2 } es regular. Claramente, forma un AP, por lo que podemos dibujar un autómata finito con 3 estados. 

   Ejemplo 4 – L = { a ^{2^n} | n>=1 } no es regular. Forma un GP, ​​por lo que no podemos tener un patrón fijo que, repetido, generaría todas las strings de este lenguaje. 
   En el ejemplo 4, si ‘n’ está acotado como n<10000, entonces se vuelve regular ya que es finito. 
    

4. No hay patrón presente, que podría repetirse para generar todas las strings en el lenguaje no es regular. Encontrar el primo en sí mismo no es posible con FA. 
   Ejemplo 5 – L = {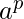  | p es primo. } no es regular. 

    

5. Una concatenación de patrón (regular) y no patrón (no regular) tampoco es un lenguaje regular. 
   Ejemplo 6 – L ₁ = {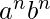  | n≥1 }, L ₂ = { n≥1 } entonces L ₁ .L ₂ no es regular. 

    

6. Siempre que se requiera almacenamiento ilimitado para almacenar el conteo y luego compararlo con otros conteos ilimitados, entonces el lenguaje no es regular. 
   Ejemplo 7 – L = {  [Tex]b^n [/Tex]| n>=1 } no es regular, porque primero necesitamos almacenar el conteo de a y luego compararlo con el conteo de b, pero el autómata finito tiene un almacenamiento limitado, pero en L, puede haber un número infinito de a entrantes, que no se puede almacenar. 

   Ejemplo 8 – L = { w | na(w) = nb(w) } no es regular. 

   Ejemplo 9 – L = { w | na(w)%3 > nb(w)%3 } es normal, porque la operación del módulo requiere un almacenamiento limitado, es decir, el módulo puede ser solo 0, 1 o 2 para la operación %3 y, de manera similar, para b, sería 0, 1 y 2. Entonces, los estados representados en DFA serían todas las combinaciones de los restos de a y b. 

    

7. Patrones de W, W ^r y x , y 
   • Si |x| está acotado a cierta longitud, entonces no es regular. 
     Ejemplo 10 – L = { W x W ^r | W, x pertenece a {a, b}* y |x|=5 } no es regular. Si W= abb entonces W ^r = bba y x = aab, entonces la string combinada es abb aab bba. Ahora, x se puede expandir para eliminar W y W ^r , pero |x| = 5. Entonces, incluso en una string expandida, W=ab, Wr=ba y x=baabb. Entonces, no obtenemos ningún patrón de forma (a+b)*, por lo que no es regular. 

      

   • Si |x| es ilimitado y W pertenece a (a+b)*, luego ponga W como épsilon y W^r como épsilon, si obtenemos (a+b)* como resultado, entonces el lenguaje es regular. 
     Ejemplo 11 – L = { W x W ^r | W, x pertenece a {a, b}* } es regular. 
     Si W = abb entonces W ^r = bba y X = aab, entonces la string combinada es abb aab bba. Ahora, x se puede expandir para eliminar W y W ^r . Así, en string expandida, W=epsilon,W ^r =epsilon y X=abb aab bba. Obtenemos un patrón simple de forma (a+b)* para el cual se puede dibujar un autómata finito. 

      

   • Si |x| es ilimitado y W pertenece a (a+b) ⁺ , luego coloque W como cualquier símbolo del alfabeto y W ^r correspondiente , si todavía podemos obtener alguna combinación de (a+b)* como resultado, con la garantía de que todas las strings será de la misma forma, entonces el lenguaje es regular sino no regular. Esto necesita más explicación con un ejemplo: 

     Ejemplo 12 – L = { W x W ^r | W, x pertenece a {a, b}+ } es regular. 
     Si W = abb entonces W ^r = bba y x = aab, entonces la string combinada es abbaabbba. Ahora, X se puede expandir para eliminar W y W ^r , dejando un símbolo a o b. En la string expandida, si W=a entonces W ^r =a y si W=b entonces W ^r =b. En el ejemplo anterior, W ^r =a. x=bbaabbb. Se reduce a las strings de patrones que comienzan y terminan en el mismo símbolo a(a+b)*a o b(a+b)*b para el cual se puede dibujar un autómata finito. 

     Ejemplo 13 – L = { WW ^r Y | W, y pertenece a {0, 1}+} no es regular. 
     Si W= 101 entonces W ^r = 101 e Y= 0111, entonces la string es 1011010111. Si y se expande, entonces W=1, W ^r =0 y y=11010111. De acuerdo con esta expansión, la string no pertenece al lenguaje en sí, eso es incorrecto, por lo tanto, no es regular. 

     Si W= 110 entonces W ^r = 011 e Y= 0111, entonces la string es 1100110111. Si y se expande, entonces W=1, Wr=1 e Y=00110111. Esta string cumple con el lenguaje, pero no podemos generalizar basándonos en esto, porque las strings también pueden comenzar con 01 y 10. 

     Ejemplo 14 – L = { x WW ^r y | x, y, W pertenece a {a, b} ⁺ } es regular. 
     Si X= aaaba, W=ab e Y=aab. La string es aaaba abbaaab. Ahora, x e y podrían expandirse de manera que W y W ^r se coman, pero dejando un símbolo para +, es decir, los nuevos valores son X= aaabaa W= b, W ^r = b. Entonces, el idioma se reduce al conjunto de todas las strings que contienen ‘bb’ o ‘aa’ como substring, lo cual es normal.