Cómo insertar strings en un árbol AVL

AVL Tree es un árbol de búsqueda binaria (BST) autoequilibrado donde la diferencia entre las alturas de los subárboles izquierdo y derecho no puede ser más de uno para todos los Nodes.

Ejemplos:

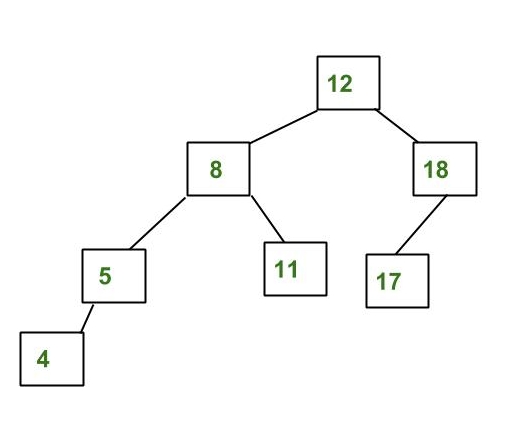
El árbol anterior es AVL porque las diferencias entre las alturas de los subárboles izquierdo y derecho para cada Node son menores o iguales a 1 . A continuación se muestra el ejemplo que no es un árbol AVL:

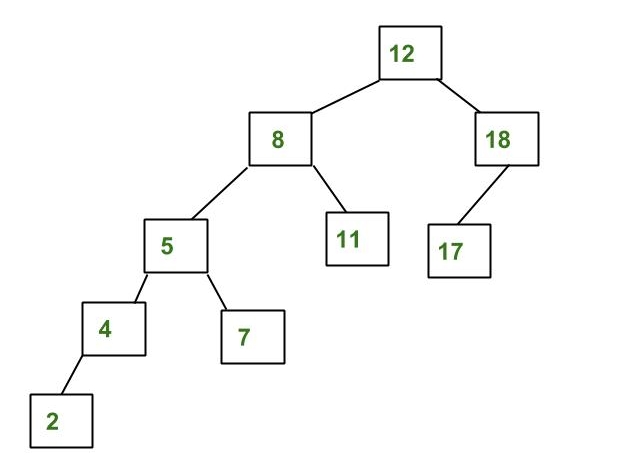
El árbol anterior no es AVL porque las diferencias entre las alturas de los subárboles izquierdo y derecho para 8 y 12 son mayores que 1. Se puede definir como un tipo de árbol de búsqueda binaria que tiene todos sus Nodes con un factor de equilibrio de -1 , 0 o 1.

Cuál es el factor de equilibrio: Es la diferencia de altura entre los dos subárboles. (Factor de equilibrio: Altura del subárbol izquierdo – Altura del subárbol derecho)

Inserción de strings en el árbol AVL :

A continuación, se muestra un ejemplo de inserción de los días de la semana en el pedido: {Martes, Lunes, Jueves, Sábado, Domingo, Viernes, Miércoles}

Acercarse:

• Si el Node está vacío ( NULL ), cree el Node con el primer valor dado.
• Si el nuevo Node es menor que el Node anterior , inserte el nuevo Node a la izquierda
• Si el nuevo Node es mayor que el Node anterior , inserte el nuevo Node a la derecha

Compruebe si el árbol está equilibrado:

• Si el factor de equilibrio es mayor que 1 , entonces puede ser:
  • Caso Izquierda-Izquierda (entonces se requiere una sola rotación para equilibrarlo).
  • O caja izquierda-derecha (se requiere doble rotación).
• Si el factor de equilibrio es menor que -1, entonces puede ser:
  • Caja derecha-derecha (se requiere una sola rotación).
  • O caja derecha-izquierda (se requiere doble rotación)

Este proceso debe repetirse para la inserción de todos los Nodes restantes.

Puntos para recordar :

• Inserte Nodes en consecuencia: para asegurarse de que el árbol dado permanezca AVL después de cada inserción, aumente la operación de inserción BST estándar para realizar un reequilibrio. Las siguientes son dos operaciones básicas que se pueden realizar para volver a equilibrar un BST sin violar la propiedad BST (keys(left) < key(root) < keys(right)) .
• Verifique el factor de equilibrio: el factor de equilibrio siempre debe ser -1, 0, 1; de lo contrario, es necesario rotar el árbol en consecuencia.

Pasos para crear un árbol AVL :

• Entonces, de acuerdo con el orden dado, insertemos Tuesday , ya que no tiene Node, por lo que tiene un factor de equilibrio de 0 .

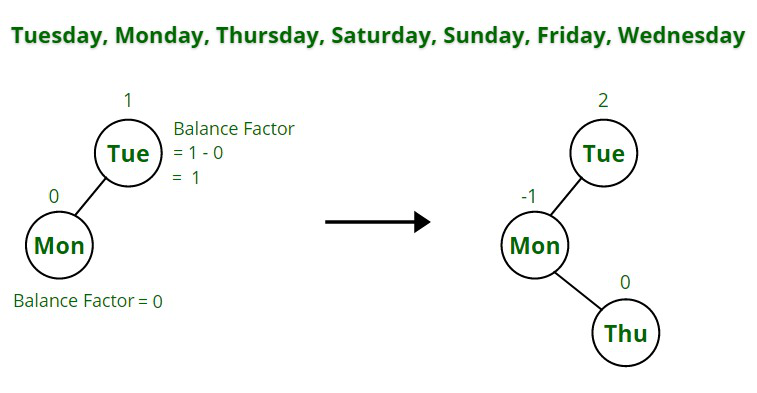
• El siguiente paso es insertar el lunes a la izquierda del martes, ya que es alfabéticamente más pequeño (M < T) . Es necesario comprobar el factor de equilibrio de cada Node antes de insertar un nuevo Node. El árbol está equilibrado como el martes porque tiene un subárbol hacia la izquierda:

Factor de equilibrio = altura del subárbol izquierdo – altura del subárbol derecho = 1 – 0 = 1

Por lo tanto, el árbol está equilibrado. El lunes también está equilibrado debido al factor de equilibrio 0.

• A continuación, inserte el jueves . Se inserta a la izquierda del martes (como Th < Tu) y se inserta a la derecha del lunes (como T>M) . Ahora, si se verifica el factor de equilibrio, se puede ver que el factor de equilibrio del martes es 2, por lo que está desequilibrado, por lo que es necesario rotar el árbol para equilibrarlo.

Nota: En caso de que no recordemos las reglas de rotación del árbol AVL, aún se puede equilibrar, solo debemos recordar que: Node izquierdo < Raíz < Node derecho .

Ejemplo:

   5 4
  / / \
 3 —–> 3 5
  \
   4

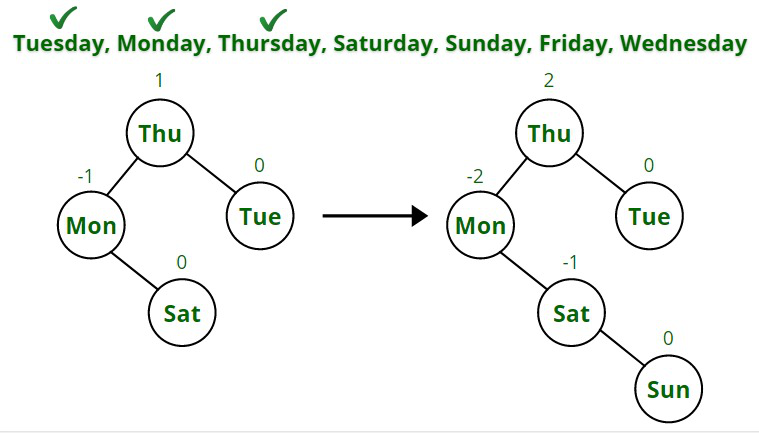
• Después de eso, inserte el sábado, a la izquierda del jueves (S < T) ya la derecha del lunes (M < S) ​​.
• El domingo se inserta a la derecha del sábado (Sa < Do) . Ahora el árbol está desequilibrado, por lo que se gira para volver a equilibrarlo.

• Se inserta el viernes siguiendo las mismas reglas y el factor de balance del jueves pasa a ser 2, por lo que se vuelve a hacer la rotación.

• Después de la rotación, ahora el último Node Wednesday se inserta a la derecha de Tuesday (como T<W).

Si el árbol AVL está marcado, ahora todo el árbol AVL está equilibrado en altura ya que todos los Nodes tienen factores de equilibrio -1 , 0 , 1 .