En MATLAB, una array se considera un conjunto bidimensional de números. Otros lenguajes de programación trabajan con números, pero en MATLAB, cada número es una array o arreglo. Para crear una array en MATLAB, los números se ingresan en cada fila agregando una coma o un espacio y el final de cada fila se marca con un punto y coma.
Supongamos que el siguiente código creó una array de 2 por 2:
Ejemplo:
Matlab
% MATLAB Code for 2x2 matrix M = [1 2 ; 3 4]
Producción:
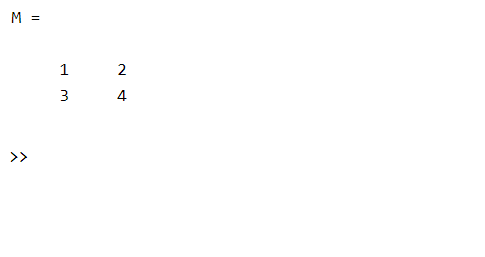
Método 1
En este método, iteramos una array cuando necesita realizar un seguimiento del índice en el que se encuentra actualmente.
Ejemplo:
Matlab
% MATLAB Code for iteration
% Create a matrix of 3-by-4 dimension
M = [2 3 4 5;
6 7 8 9 ;
0 1 6 8];
% Get rows and columns of matrix using
% size() function
[rows,column]=size(M);
% Iterate through each row and display
% each column element of that row
for i=1:rows
for j=1:column
x=M(i,j);
fprintf( ' %d ',x);
end
% Add a line break after one row is displayed
fprintf('\n');
end
Producción:

array de salida
Método 2
El método anterior para iterar una array se usa cuando necesita realizar un seguimiento del índice en el que se encuentra actualmente. Hay otra forma de iterar una array usando un punto y coma. En la array, como se discutió anteriormente, se puede acceder a cada elemento especificando su posición en la array. Si desea iterar a través de algunos elementos específicos, use la indexación basada en rangos como se ilustra a continuación:
Ejemplo 1:
Matlab
% MATLAB Code for iteration using semicolon % Create a matrix of 3-by-4 dimension M=[2 3 4 5; 6 7 8 9 ; 0 1 6 8]; %Most often in matrix we use vectors subscripts % to access elements in specific range. For example % to access rows 2nd and 3rd, 1st and 2nd column use indexing as: M(2:3,1:2) %2:3 specifies that extract elements of 2nd and 3rd row %1:2 for column index tells to extract 1st and 2nd column elements.
Producción:

PRODUCCIÓN
De manera similar, toda la array se puede iterar utilizando la indexación basada en rangos como:
Ejemplo 2:
Matlab
% MATLAB Code for the whole matrix iteration % by using range based indexing % Create a matrix of 3-by-4 dimension M=[2 3 4 5; 6 7 8 9 ; 0 1 6 8]; %similarly if you want to iterate through whole matrix, just specify its %rows and columns M(1:3,1:4)%iterate through rows 1-3 and column 1-4.
Producción:
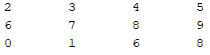
PRODUCCIÓN
Ampliando la idea anterior, toda la array se puede iterar sin definir explícitamente los vectores de rango, como se muestra a continuación:
Ejemplo 3:
Matlab
% MATLAB Code for whole matrix can be iterated % without explicitly defining range vectors %Create a matrix of 3-by-4 dimension M=[2 3 4 5; 6 7 8 9 ; 0 1 6 8]; %Leave rows and column place as empty and % MATLAB takes it as 'all' M(:,:) %whole matrix iterated.
Producción:
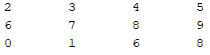
PRODUCCIÓN
Método 3
En MATLAB hay una función numel que puede dar el número de elementos en una array. Usándolo, itere a través de la array y muestre cada elemento de la array como se muestra a continuación:
Ejemplo:
Matlab
% MATLAB Code for iteration using numel() % Create a matrix of 3-by-4 dimension M=[2 3 4 5; 6 7 8 9 ; 0 1 6 8]; % create output vector for storing outputs output=[]; % get number of elements in matrix M n=numel(M); % loop through all elements and store values in output array. for i=1:n output(i)=M(i); end % prints output array. output
Producción:
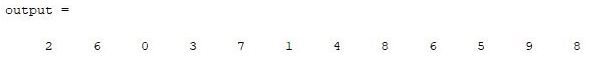
PRODUCCIÓN
Aquí el resultado es diferente al anterior porque se accede a los elementos de una array por columnas. A medida que el ciclo va de 1 a un número de elementos en la array, se accede a cada elemento según su índice. La tabla muestra la indexación lineal de cada elemento en la array MATLAB.
| 1 | 4 | 7 | 10 |
| 2 | 5 | 8 | 11 |
| 3 | 6 | 9 | 12 |
Publicación traducida automáticamente
Artículo escrito por alijohnnaqvi6 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA