El algoritmo RSA es un algoritmo criptográfico asimétrico, lo que significa que debe haber dos claves involucradas durante la comunicación, es decir, clave pública y clave privada. Hay pasos simples para resolver problemas en el Algoritmo RSA.
Ejemplo 1:
- Paso 1: Elija dos números primos
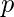 y
y 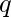
Tomemos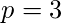 y
y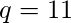
- Paso 2: Calcule el valor de
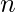 y
y 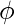
se da como,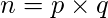 and
and 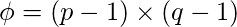
Aquí en el ejemplo,
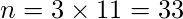

- Paso 3: Encuentre el valor de
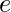 (clave pública)
(clave pública)
Elija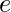 , de modo que
, de modo que 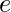 debería ser coprincipal. Co-prime significa que no debe multiplicarse por factores de
debería ser coprincipal. Co-prime significa que no debe multiplicarse por factores de 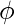 y tampoco dividirse por
y tampoco dividirse por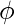
Los factores de
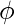 son,
son,  por lo
por lo 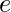 que no deben multiplicarse por
que no deben multiplicarse por 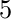 y
y 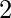 no deben dividirse por 20.
no deben dividirse por 20.Entonces, los primos son 3, 7, 11, 17, 19…, como se toman 3 y 11 se elige
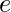 como 7
como 7Por lo tanto,
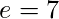
- Paso 4: Calcule el valor de
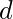 (clave privada)
(clave privada)
La condición se da como,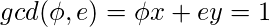 donde y es el valor de
donde y es el valor de 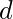 .
.
Para calcular el valor de
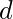 ,
,- Forme una tabla con cuatro columnas, es decir, a, b, d y k.
- Inicialice a = 1, b = 0, d =
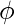 , k = – en la primera fila.
, k = – en la primera fila. - Inicialice a = 0, b = 1, d =
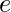 ,
, 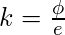 en la segunda fila.
en la segunda fila. - Desde la siguiente fila, aplique las siguientes fórmulas para encontrar el valor de los siguientes a, b, d y k, que se da como
Tan pronto como,
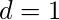 detenga el proceso y verifique la siguiente condición
detenga el proceso y verifique la siguiente condiciónif

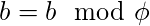 if
if 

Para un ejemplo dado, la tabla será,
a b d k 1 0 20 – 0 1 7 2 1 -2 6 1 -1 3 1 – Como en la tabla anterior
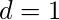 , detenga el proceso y verifique la condición dada para el
, detenga el proceso y verifique la condición dada para el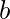

Para verificar que
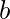 es correcto, la condición anterior debe cumplirse, es decir,
es correcto, la condición anterior debe cumplirse, es decir, 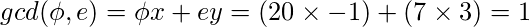 . Por lo tanto
. Por lo tanto 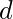 es correcto.
es correcto. - Paso 5: realice el cifrado y el descifrado
El cifrado se proporciona como, el
descifrado se proporciona como,
Para el ejemplo dado, supongamos
 que el
que el
cifrado es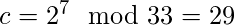
El descifrado es

Por lo tanto, en la final,
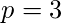 ,
, 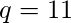 ,
, 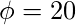 ,
,  ,
, 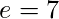 y
y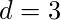
Ejemplo-2: GATE CS-2017 (Conjunto 1)
En un criptosistema RSA, un A en particular usa dos números primos p = 13 y q = 17 para generar sus claves públicas y privadas. Si la clave pública de A es 35. ¿Entonces la clave privada de A es?
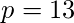 y
y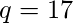
- Calcular
 y
y
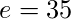 (Llave pública)
(Llave pública)- Calcular
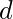 (clave privada)
(clave privada)
a b d k 1 0 192 – 0 1 35 5 1 -5 17 2 -2 11 1 – 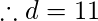 (llave privada)
(llave privada)
Publicación traducida automáticamente
Artículo escrito por bilal-hungund y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA