¿Cómo sumar fracciones con números negativos?

Una fracción es un valor numérico que se define como parte de un todo. Se deriva de la palabra ‘fractio’ que significa romper. Se usa para resolver problemas de la vida diaria, como dividir alimentos, suministros, dinero, etc. Un número que tiene la forma a/b se puede llamar fracción. Donde a, b son números cualesquiera. Por ejemplo, 2/3, 12/4, etc. Los números racionales e irracionales que tienen la forma a/b pueden considerarse fracciones.

Parte de fracción

La fracción consta de dos partes:

• Denominador: La parte más baja de la fracción se conoce como denominador. Representa en cuántas partes se dividirá el número entero dado. Por ejemplo, 2/3, aquí 3 se conoce como denominador.
• Numerador: La parte superior de la fracción se conoce como numerador. Representa en qué cuántos tramos de la fracción. Por ejemplo, 2/3, aquí 3 se conoce como numerador

Tipo de fracción

Los siguientes son los tipos de fracciones:

• Fracción Propia: Las fracciones propias son aquellas fracciones en las que el numerador siempre es menor que su denominador. Por ejemplo, 5/16, 1/4, etc.
• Fracción impropia: Las fracciones impropias son aquellas fracciones en las que el numerador siempre es mayor o igual que su denominador. Por ejemplo, 5/2, 11/4, etc.
• Fracción Unitaria: Las fracciones unitarias son aquellas fracciones que tienen solo 1 en el numerador. Por ejemplo, 1/2, 1/14, etc.
• Fracción mixta: Las fracciones mixtas son aquellas fracciones que contienen la mezcla de fracciones enteras y propias. Por ejemplo, 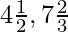 etc
• Fracción equivalente: Las fracciones equivalentes son aquellas fracciones que contienen los mismos valores. Por ejemplo, 2/9 x 2/2 = 4/18.
• Fracción igual: Las fracciones iguales son aquellas fracciones que contienen los mismos denominadores. Por ejemplo, 2/8, 4/8, etc.
• Fracción diferente: Las fracciones diferentes son aquellas fracciones que contienen diferentes denominadores. Por ejemplo, 2/9, 8/13, etc.

Sumar fracciones con Números Negativos

Como sabemos, la suma es la operación básica de las matemáticas. Se utiliza para encontrar la suma de dos números positivos o negativos. También podemos sumar fracciones con igual o distinto denominador. También se nos permite sumar fracciones con números negativos. Algunas reglas que debemos recordar cuando realizamos sumas o restas entre números positivos o negativos. Los que se mencionan a continuación-

Regla 1: Cuando se multiplican dos números positivos obtenemos un resultado positivo.

(+) x (+) = +

Ejemplo: 5×2=10

Regla 2: cuando se multiplican dos números/símbolos negativos, obtenemos un resultado positivo.

(-) x (-) = +

Ejemplo: (-7)×(-2)= 14

Aquí dos símbolos negativos se cancelan entre sí.

Regla 3: Cuando se multiplican números enteros positivos y negativos, el número resultante será negativo.

(-) x (+) = –

Ejemplo: (-7) x 2 = -14

Entonces, debemos considerar estas reglas al realizar la suma entre fracciones y números negativos. 

Pasos para sumar fracciones con números negativos:

Tenemos una fracción a/b y un número negativo -c. Ahora los agregamos usando los siguientes pasos:

Paso 1: Convierte sus símbolos de acuerdo con la regla anterior. Aquí, a/b + (-c) = a/b – c

Paso 2: a/b – c también puede escribirse como a/b -c/1

Paso 3: ahora toma el LCM en b y 1

Paso 4: Ahora la ecuación final es (a – c)/b y resuelve esta ecuación para obtener el resultado final. 

Ejemplos de preguntas

Pregunta 1: (1/2) + (-1) = ?

Solución:

Aquí tenemos la operación + antes de un número negativo. De acuerdo con la regla 3, cuando multiplicamos + por – obtenemos un símbolo negativo.

(1/2) + (-1) se convertirá en (1/2) – 1

 Este (1/2) – 1 se puede reescribir en (1/2) – (1/1)

MCM de 2 denominadores 2,1 es 2.

(1/2) – (1/1) = (1 – 2)/2

= -1/2 

= -0.5

Pregunta 2: -(1/2) + (-1) = ?

Solución:

Aquí tenemos la operación + antes de un número negativo. De acuerdo con la regla 3, cuando multiplicamos + por – obtenemos un símbolo negativo.

-(1/2) + (-1) se convertirá en -(1/2) – 1

Este -(1/2) – 1 se puede reescribir en (-1/2) – (1/1)

MCM de 2 denominadores 2,1 es 2.

(-1/2) – (1/1) = (-1 – 2)/2

= -3/2 

= -1.5

Pregunta 3: -(1/3) + (3/6) = ?

Solución:

MCM de 2 denominadores 3, 6 es 6.

(-1/3) + (3/6) = (-2 + 3)/6

= 1/6 

Pregunta 4: -(1/3) + (3/8) = ?

Solución:

MCM de 2 denominadores 3,8 es 24.

(-1/3) + (3/8) = ( (-1×8) + (3×3) )/24

=(-8 + 9) /24

= 1/24

Pregunta 5: -(1/3) + (-2) = ?

Solución:

Aquí tenemos la operación + antes de un número negativo. De acuerdo con la regla 3, cuando multiplicamos + por – obtenemos un símbolo negativo.

(-1/3) + (-2) se convertirá en (-1/3)-(2)

Este -(1/3) – 2 se puede reescribir como (-1/3) – (2/1)

MCM de 2 denominadores 3, 1 es 3.

(-1/3) – (2/1) = (-1 – 2)/3

= -3/3

= -1