La correlación es un concepto que proviene del trasfondo de las estadísticas. En términos estadísticos, la correlación se puede definir como la asociación lineal entre dos entidades. Simplemente, se puede entender como el cambio en una entidad conduce a cuánto cambia la proporción en otra entidad. Muchas veces, la correlación se confunde con otro término popular en las estadísticas, la causalidad . Para diferenciar y aclarar, uno debe entender que la correlación no provoca un cambio en los valores de la segunda entidad cuando los valores de la primera entidad cambian y viceversa.
Entendamos esta diferencia con la ayuda de un ejemplo. Muchas veces se ha observado que durante la temporada de verano los índices de delincuencia suelen aumentar en una ciudad y también durante la temporada de verano hay un aumento en la venta de helados. Podemos entender fácilmente que debido al aumento de la temperatura, las personas tienden a preferir alimentos más fríos para relajarse del calor, lo que provoca un aumento en las ventas de helados. Por lo tanto, esta es una causa común de causalidad, mientras que cuando comparamos el aumento en la venta de helados con el aumento en la tasa de delincuencia durante el verano, ambos están correlacionados pero uno no es la causa del otro.
Ahora, puede haber una correlación positiva o una correlación negativa entre dos entidades. El grado de correlación a menudo se proporciona mediante un coeficiente de correlación denominado coeficiente de correlación de Pearson, que lleva el nombre de Karl Pearson, quien dio el concepto de correlación. La fórmula estadística para el coeficiente de Pearson se da como:
![]()
Donde x e y son dos entidades separadas, Cov(x,y) es la covarianza entre dos entidades x e y, σ x y σ y es la desviación estándar de x e y respectivamente. Para saber más sobre la ecuación matemática y cómo se usa, puede consultar https://www.geeksforgeeks.org
Correlación en Excel
El valor del coeficiente de correlación varía de -1 a +1. Cuanto más cerca esté el valor de -1 o +1, tanto más se relacionarán ambas entidades entre sí. Si el coeficiente de correlación resulta ser 0, decimos que no existe una relación lineal entre ambas entidades. Entendamos esto con la ayuda de un ejemplo en el que calcularemos el coeficiente de correlación de Pearson usando Excel. Supongamos que tenemos registros de altura y peso de 10 estudiantes de una clase que se da como:
| Altura (en cm) | Peso (en kg) |
|---|---|
|
155 |
66 |
|
178 |
82 |
|
148 |
62 |
|
162 |
70 |
|
165 |
71 |
|
172 |
74 |
|
158 |
64 |
|
152 |
sesenta y cinco |
|
176 |
80 |
|
185 |
93 |
Podemos calcular la correlación en Excel usando dos métodos:
Método 1: Usar la función CORREL()
Excel tiene una función CORREL() incorporada que se puede usar para calcular el coeficiente de correlación de Pearson. La sintaxis básica para CORREL() se da como:
=CORREL(array1, array2)
Donde array1 y array2 son las arrays de registros de la primera entidad y la segunda entidad respectivamente.
Paso 1: Podemos calcular el coeficiente de correlación entre ambos atributos utilizando la fórmula aplicada en la celda A13, es decir,
=CORREL(A2:A11, B2:B11)
Pasamos la primera array, Altura (en cm) de A2:A11 como primer parámetro, y la segunda array, Peso (en kg) de B2:B11 como segundo parámetro dentro de la fórmula CORREL().
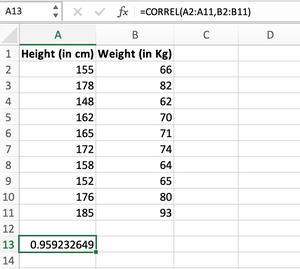
Uso de la función CORREL() para calcular el coeficiente de correlación de Pearson
El valor obtenido después de calcular el coeficiente de correlación resulta ser 0.959232649 que es muy cercano a +1, por lo que podemos concluir que la altura y el peso del estudiante están altamente correlacionados positivamente entre sí. Es probable que podamos decir que si un estudiante es más alto, entonces hay mayores posibilidades de que el estudiante también tenga un peso más alto.
A continuación también se muestra un video que demuestra todo el uso de la función CORREL() para calcular el valor de correlación.
Método 2: Uso de la herramienta de análisis de datos
Paso 1: en la barra de menú, seleccione la pestaña Datos.

Paso 2: En la pestaña de datos, seleccione la opción Análisis de datos.

Paso 3: Aparecerá un cuadro de diálogo de herramientas de análisis de datos, en el cuadro de diálogo seleccione la opción Correlación.
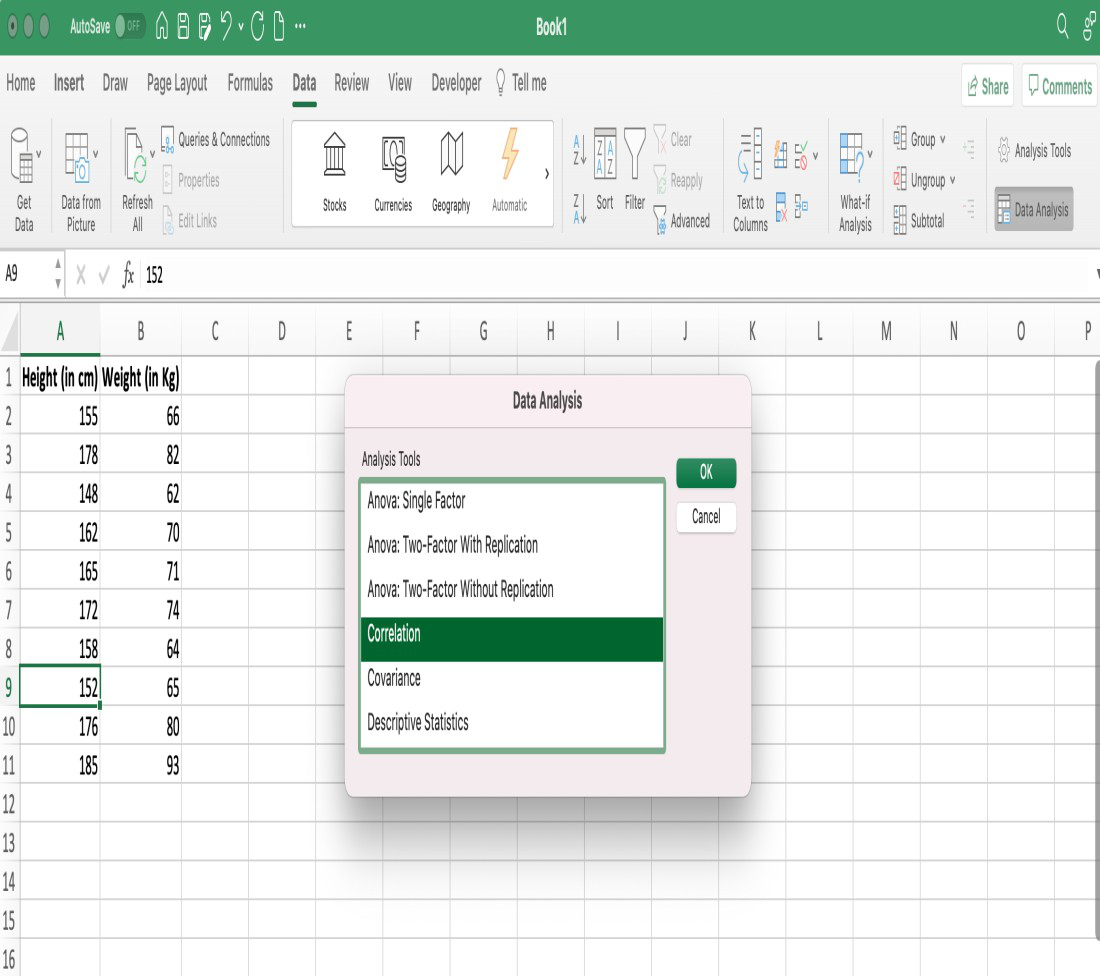
Cuadro de diálogo Análisis de datos
Paso 4: aparecerá un cuadro de diálogo adicional para la correlación, en el cuadro de diálogo primero tenemos que dar el rango de entrada, así que seleccione toda la tabla. Como nuestros datos están agrupados por Columnas seleccionaremos la opción Columnas . Además, nuestros datos tienen etiquetas en la primera fila, por lo tanto, haremos clic en la casilla de verificación que dice Etiquetas en la primera fila . Podemos obtener resultados según nuestros requisitos en la hoja actual o en una nueva hoja de trabajo o en un nuevo libro de trabajo. Podemos seleccionar la opción de nueva hoja de trabajo y hacer clic en el botón Aceptar.
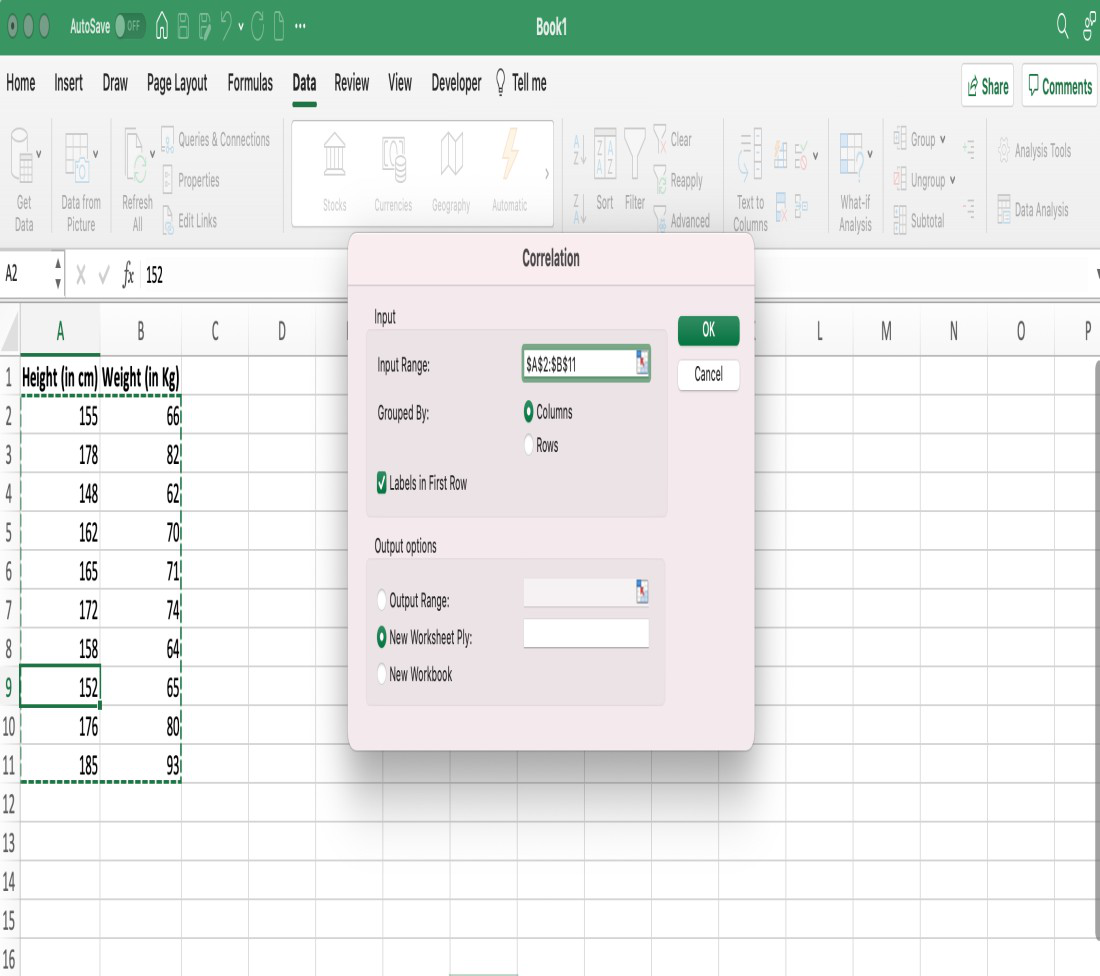
Llenar todos los valores dentro del cuadro de diálogo de correlación
Paso 5: La salida se generará automáticamente en la nueva hoja de trabajo.
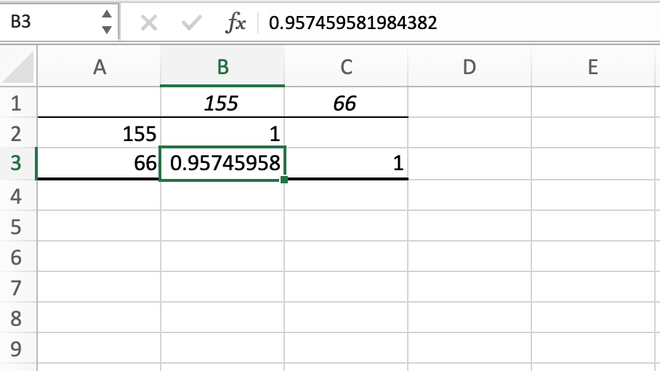
Tabla de correlación generada con la herramienta de análisis de datos
A continuación también se muestra un video que demuestra todos los pasos anteriores para calcular el valor de correlación.
A partir de la nueva hoja de trabajo, podemos notar que se generará una tabla de correlación en la que podemos ver que nuestro valor de correlación entre la altura y el peso es 0.959232649 , que también obtuvimos usando el primer método.
Publicación traducida automáticamente
Artículo escrito por saurabh48782 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA