Comparación entre el árbol equilibrado en altura y el árbol equilibrado en peso

¿Qué es el árbol de altura equilibrada?

Los árboles de búsqueda binarios autoequilibrados son árboles binarios de altura equilibrada en los que, en cada Node, el valor absoluto de la diferencia de alturas del subárbol izquierdo y derecho no es mayor que uno. Un árbol vacío está equilibrado en altura. Un árbol binario T no vacío está balanceado si:  

1. El subárbol izquierdo de T está balanceado.
2. El subárbol derecho de T está balanceado.
3. La diferencia entre las alturas del subárbol izquierdo y el subárbol derecho no es más de 1.

Nota: 

Todo árbol binario completo está equilibrado en altura.

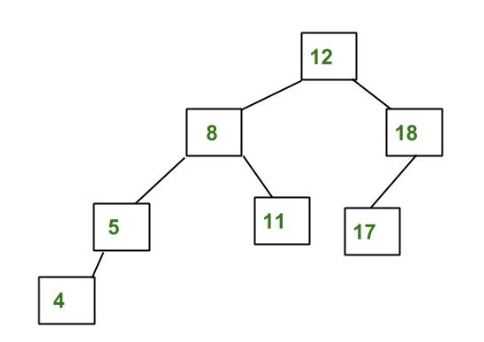
Ejemplo: 

Red Black Tree, Splay Tree y AVL Tree es un árbol de búsqueda binaria de altura equilibrada.

¿Qué es el árbol binario de peso equilibrado?

Un árbol de peso equilibrado es un árbol binario en el que para cada Node el número de Nodes en el subárbol izquierdo es al menos la mitad y como máximo el doble del número de Nodes en el subárbol derecho. Es un árbol binario que se equilibra en base al conocimiento de las probabilidades de búsqueda de cada Node individual. En cada subárbol, el Node con el mayor peso aparece en la raíz, lo que da como resultado un rendimiento de búsqueda más eficiente. Los Nodes que tienen más probabilidades de ser buscados/accedidos tienen el tiempo de búsqueda más bajo.

Ejemplo:

Árbol de Huffmann.

En el diagrama anterior, las letras representan los valores de los Nodes y los números representan los pesos de los Nodes.

¿Por qué diferentes definiciones de equilibrado?

El árbol de búsqueda binaria (BST) se inventó para hacer que la búsqueda sea un proceso más eficiente que buscar en una array desordenada. Sin embargo, cuando el BST está desequilibrado, la búsqueda de casos fue ineficaz. Para una búsqueda eficiente, es recomendable mantener el árbol equilibrado. Pero es difícil e ineficiente mantener un BST equilibrado ya que los valores se agregan y eliminan con frecuencia. Por lo tanto, se inventó una forma de mantener el BST equilibrado agregando más información a cada Node o permitiendo que un Node tenga más de dos hijos. Algunos de los ejemplos de tales árboles inventados fueron AVL Tree, 2-3 Tree, B-Tree, Red-Black Tree, etc.

Comparación de árbol equilibrado en altura y equilibrado en peso

Un árbol de altura equilibrada mejora el tiempo de búsqueda en el peor de los casos (para un árbol binario, siempre estará delimitado por log2(n)), a expensas de hacer que el caso típico sea aproximadamente una búsqueda menos (aproximadamente la mitad de los Nodes serán a la máxima profundidad).

Si su peso está relacionado con la frecuencia de búsqueda, un árbol de peso equilibrado mejorará el tiempo promedio de búsqueda, a expensas de hacer que el peor de los casos sea más alto (los elementos solicitados con más frecuencia tienen un peso más alto y, por lo tanto, tenderán a ser en árboles menos profundos, con el costo de árboles más profundos para artículos solicitados con menos frecuencia).

No. S.	Árbol equilibrado en altura	Árbol de peso equilibrado
1	Es el árbol binario que se equilibra en función de la altura de los subárboles.	Es el árbol binario que se equilibra en función del peso en los bordes del árbol.
2	En un árbol de altura equilibrada, la diferencia absoluta de altura del subárbol izquierdo y el subárbol derecho debe ser mínima.	En el árbol de peso equilibrado, la diferencia absoluta entre el peso del subárbol izquierdo y el subárbol derecho debe ser mínima.
3	Mejorará el tiempo de búsqueda en el peor de los casos a expensas de hacer que un caso típico sea aproximadamente una búsqueda menos	Mejorará el tiempo promedio de búsqueda a expensas de hacer que el peor de los casos sea más alto.
4	La operación de reestructuración en un Node con n descendientes ocurre cada operación 2 -O(lg n) .	La operación de reestructuración en un Node con n descendientes ocurre cada operación O(1/n).

¿Cuál es el mejor?

La mejor manera de determinar cuál es el mejor árbol de búsqueda binario de los dos es medir el rendimiento de los dos árboles. Esto se puede hacer en los siguientes pasos:

1. Recopile tráfico de consultas representativo.
2. Construya un banco de pruebas donde se puedan contar las operaciones del árbol.
3. Vuelva a reproducir las consultas enlatadas contra un árbol de altura equilibrada y un árbol de peso equilibrado.

Como regla general, un árbol de altura equilibrada funcionaría mejor cuanto más uniformes sean las frecuencias de solicitud en el conjunto de datos, y cuanto más sesgado esté, más ventajas se pueden obtener de un árbol de peso equilibrado.