Un gráfico es una estructura de datos no lineal que consta de Nodes y bordes. Los Nodes a veces también se conocen como vértices y los bordes son líneas o arcos que conectan dos Nodes en el gráfico. En este artículo, entenderemos la diferencia entre las formas de representación del gráfico.
Un gráfico se puede representar principalmente de dos formas. Están:
- Lista de adyacencia: una lista de adyacencia es una array que consta de la dirección de todas las listas vinculadas . El primer Node de la lista enlazada representa el vértice y las listas restantes conectadas a este Node representan los vértices a los que está conectado este Node. Esta representación también se puede utilizar para representar un gráfico ponderado. La lista vinculada se puede cambiar ligeramente para almacenar incluso el peso del borde.
- Array de adyacencia: La array de adyacencia es una array 2D de tamaño V x V donde V es el número de vértices en un gráfico. Sea la array 2D adj[][], una ranura adj[i][j] = 1 indica que hay una arista desde el vértice i hasta el vértice j. La array de adyacencia para el gráfico no dirigido siempre es simétrica. La array de adyacencia también se utiliza para representar gráficos ponderados. Si adj[i][j] = w, entonces hay una arista del vértice i al vértice j con peso w.
Consideremos un gráfico para comprender la lista de adyacencia y la representación de la array de adyacencia. Sea el grafo no dirigido:
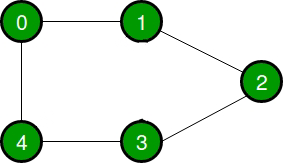
El siguiente gráfico se representa en las representaciones anteriores como:
- Array de adyacencia: en la representación de array de adyacencia, un gráfico se representa en forma de array bidimensional. El tamaño de la array es V x V , donde V es el conjunto de vértices. La siguiente imagen representa la representación de la array de adyacencia:

- Lista de adyacencia: en la representación de la lista de adyacencia, un gráfico se representa como una array de lista enlazada. El índice de la array representa un vértice y cada elemento en su lista enlazada representa los vértices que forman un borde con el vértice. La siguiente imagen representa la representación de la lista de adyacencia:
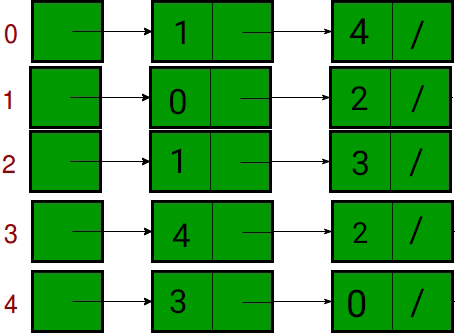
La siguiente tabla describe la diferencia entre la array de adyacencia y la lista de adyacencia:
| Operaciones | Array de adyacencia | Lista de adyacencia |
|---|---|---|
| Espacio de almacenamiento | Esta representación hace uso de la array VxV, por lo que el espacio requerido en el peor de los casos es O(|V| 2 ) . | En esta representación, para cada vértice almacenamos sus vecinos. En el peor de los casos, si un gráfico está conectado, se requiere O(V) para un vértice y O(E) para almacenar los vecinos correspondientes a cada vértice. Por lo tanto, la complejidad total del espacio es O(|V|+|E|) . |
| Agregar un vértice | Para agregar un nuevo vértice a la array VxV, el almacenamiento debe aumentarse a (|V|+1) 2 . Para lograr esto, necesitamos copiar toda la array. Por lo tanto la complejidad es O(|V| 2 ) . | Hay dos punteros en la lista de adyacencia, el primero apunta al Node frontal y el otro apunta al Node posterior. Por lo tanto, la inserción de un vértice se puede realizar directamente en el tiempo O (1). |
| Agregar un borde | Para agregar una arista, digamos de i a j, matrix[i][j] = 1, lo que requiere O(1) tiempo. | Similar a la inserción de vértice aquí, también se usan dos punteros que apuntan al frente y al final de la lista. Por lo tanto, se puede insertar un borde en el tiempo O(1) . |
| Quitar un vértice | Para eliminar un vértice de la array V*V, el almacenamiento debe reducirse a |V| 2 de (|V|+1) 2 . Para lograr esto, necesitamos copiar toda la array. Por lo tanto la complejidad es O(|V| 2 ) . | Para eliminar un vértice, debemos buscar el vértice que requerirá un tiempo O(|V|) en el peor de los casos, después de esto, debemos atravesar los bordes y, en el peor de los casos, requerirá un tiempo O(|E|) .Por lo tanto, la complejidad del tiempo total es O(|V|+|E|) . |
| Eliminación de un borde | Para eliminar una arista, digamos de i a j, matrix[i][j] = 0, lo que requiere O(1) tiempo. | Para eliminar un borde, se requiere atravesar los bordes y, en el peor de los casos, necesitamos atravesar todos los bordes. Por lo tanto, la complejidad del tiempo es O(|E|) . |
| consultando | Para encontrar un borde existente, se debe verificar el contenido de la array. Dados dos vértices, digamos i y j, la array [i] [j] se puede verificar en tiempo O (1) . | En una lista de adyacencia, cada vértice está asociado con una lista de vértices adyacentes. Para un gráfico dado, para verificar un borde, debemos verificar los vértices adyacentes al vértice dado. Un vértice puede tener como máximo vecinos O(|V|) y, en el peor de los casos, tendríamos que comprobar todos los vértices adyacentes. Por lo tanto, la complejidad del tiempo es O(|V|) . |