Un comparador digital de magnitud es un circuito combinacional que compara dos números digitales o binarios para averiguar si un número binario es igual, menor o mayor que el otro número binario. Diseñamos lógicamente un circuito para el cual tendremos dos entradas una para A y otra para B y tres terminales de salida, una para la condición A > B, una para la condición A = B y otra para la condición A < B.
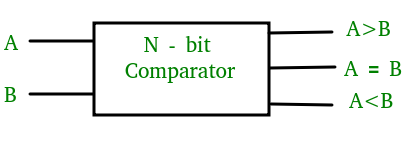
Comparador de magnitud de 1 bit:
Un comparador utilizado para comparar dos bits se denomina comparador de un solo bit. Consta de dos entradas cada una para dos números de un solo bit y tres salidas para generar menor que, igual a y mayor que entre dos números binarios.
La tabla de verdad para un comparador de 1 bit se muestra a continuación:
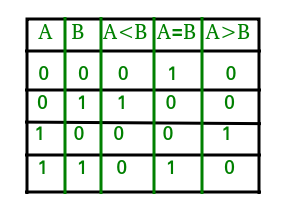
From the above truth table logical expressions for each output can be expressed as follows:
A>B: AB' A<B: A'B A=B: A'B' + AB
De las expresiones anteriores podemos derivar la siguiente fórmula:

Al usar estas expresiones booleanas, podemos implementar un circuito lógico para este comparador como se indica a continuación:
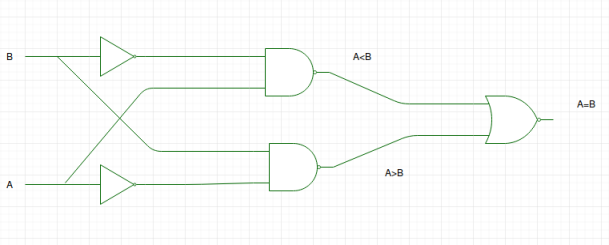
El diagrama lógico está mal
Comparador de magnitud de 2 bits:
Un comparador que se utiliza para comparar dos números binarios cada uno de dos bits se denomina comparador de magnitud de 2 bits. Consta de cuatro entradas y tres salidas para generar menor que, igual y mayor que entre dos números binarios.
La tabla de verdad para un comparador de 2 bits se muestra a continuación:
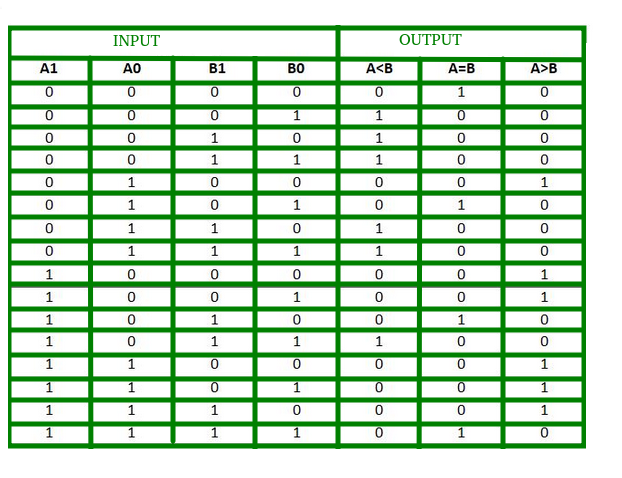
De la tabla de verdad anterior, el mapa K para cada salida se puede dibujar de la siguiente manera:



De las expresiones lógicas de K-maps anteriores para cada salida se pueden expresar de la siguiente manera:
A>B:A1B1’ + A0B1’B0’ + A1A0B0’ A=B: A1’A0’B1’B0’ + A1’A0B1’B0 + A1A0B1B0 + A1A0’B1B0’ : A1’B1’ (A0’B0’ + A0B0) + A1B1 (A0B0 + A0’B0’) : (A0B0 + A0’B0’) (A1B1 + A1’B1’) : (A0 Ex-Nor B0) (A1 Ex-Nor B1) A<B:A1’B1 + A0’B1B0 + A1’A0’B0
Al usar estas expresiones booleanas, podemos implementar un circuito lógico para este comparador como se indica a continuación:
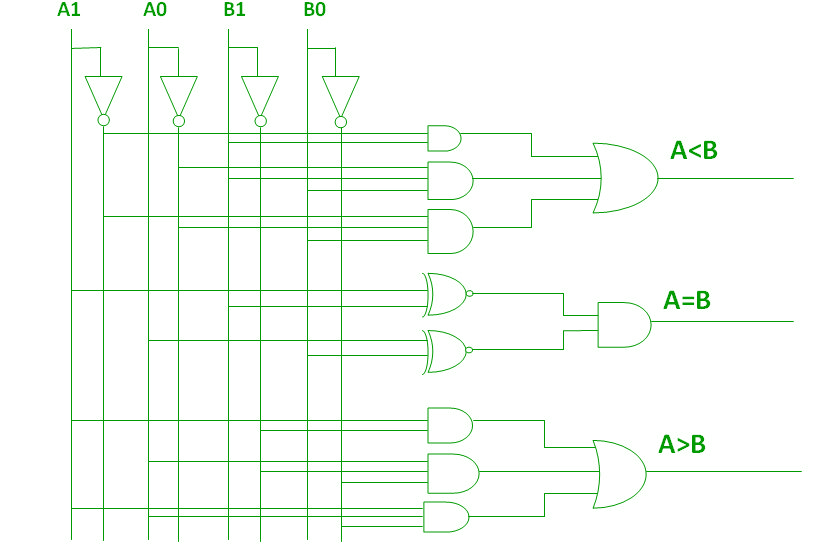
Comparador de magnitud de 4 bits:
Un comparador utilizado para comparar dos números binarios cada uno de cuatro bits se denomina comparador de magnitud de 4 bits. Consta de ocho entradas cada una para dos números de cuatro bits y tres salidas para generar menor que, igual que y mayor que entre dos números binarios.
En un comparador de 4 bits, la condición de A>B puede ser posible en los siguientes cuatro casos:
- Si A3 = 1 y B3 = 0
- Si A3 = B3 y A2 = 1 y B2 = 0
- Si A3 = B3, A2 = B2 y A1 = 1 y B1 = 0
- Si A3 = B3, A2 = B2, A1 = B1 y A0 = 1 y B0 = 0
De manera similar, la condición para A<B puede ser posible en los siguientes cuatro casos:
- Si A3 = 0 y B3 = 1
- Si A3 = B3 y A2 = 0 y B2 = 1
- Si A3 = B3, A2 = B2 y A1 = 0 y B1 = 1
- Si A3 = B3, A2 = B2, A1 = B1 y A0 = 0 y B0 = 1
La condición de A=B solo es posible cuando todos los bits individuales de un número coinciden exactamente con los bits correspondientes de otro número.
A partir de las declaraciones anteriores, las expresiones lógicas para cada salida se pueden expresar de la siguiente manera:
AA, 831331 r: (A3 EioNor 33)A2132′ a (A3 Ex-Nor 133) (A2 Ex-Nor 132)A131′ a (A3 Ex-Nor 33) (A2 ENor132) (Al Ex-Nor 31)A01301
, 13: A3’03 a (A3 Ex-Nor 33)A211:12 a (A3 Ex-Nor 83) (A2 Ex-Nor 132)Ar131 a (A3 Ex-Nor 33) (A2 Ex-Nor32) (Al Ex- Ni 131)A0N30
A=B: (A3 Ex-Nor B3) (A2 Ex-Nor 82) (Al Ex-Nor BI) (AO Ex-Nor BO)
Al usar estas expresiones booleanas, podemos implementar un circuito lógico para este comparador como se indica a continuación:
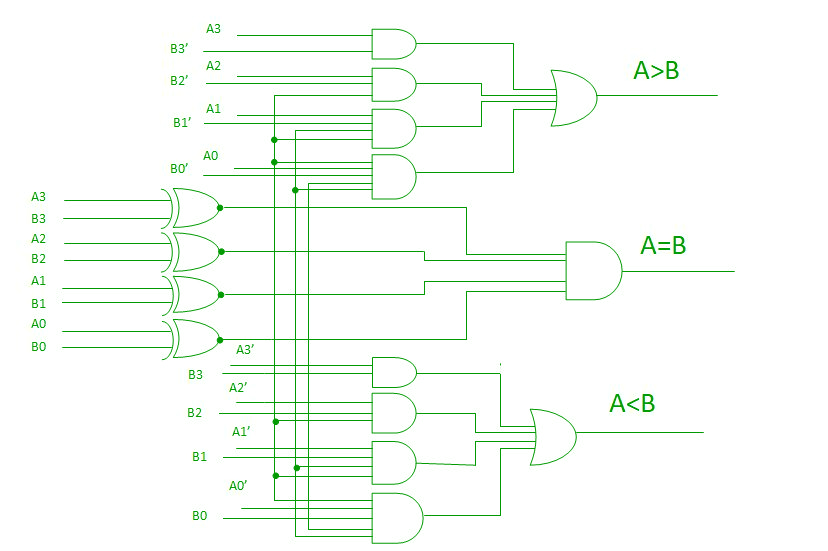
NOTA:
Para n- el comparador de bits entonces, el número de combinaciones para las cuales
- A = B es 2 norte
- A > B o A < B es (2 2n – 2 n )/2
Comparador en cascada:
Un comparador que realiza la operación de comparación a más de cuatro bits mediante la conexión en cascada de dos o más comparadores de 4 bits se denomina comparador en cascada. Cuando se van a conectar en cascada dos comparadores, las salidas del comparador de orden inferior se conectan a las entradas correspondientes del comparador de orden superior.
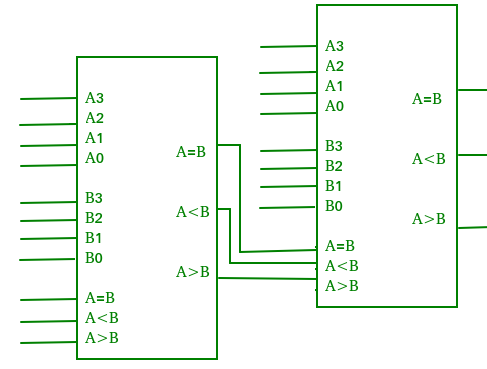
Aplicaciones de los comparadores:
- Los comparadores se utilizan en unidades centrales de procesamiento (CPU) y microcontroladores (MCU).
- Se utilizan en aplicaciones de control en las que los números binarios que representan variables físicas como temperatura, posición, etc. se comparan con un valor de referencia.
- Los comparadores también se utilizan como controladores de procesos y para el control de servomotores.
- Se utiliza en la verificación de contraseñas y aplicaciones biométricas.
Publicación traducida automáticamente
Artículo escrito por Harshita Pandey y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA