Complejidad de diferentes operaciones en árbol binario, árbol de búsqueda binaria y árbol AVL

En este artículo, discutiremos la complejidad de diferentes operaciones en árboles binarios, incluidos los árboles BST y AVL. Antes de comprender este artículo, debe tener una idea básica sobre: ​​árbol binario, árbol de búsqueda binaria y árbol AVL .

Las operaciones principales en el árbol binario son: buscar, insertar y eliminar. Veremos la complejidad temporal del peor caso de estas operaciones en árboles binarios.

Árbol binario:
en un árbol binario, un Node puede tener un máximo de dos hijos. Considere el árbol binario sesgado a la izquierda que se muestra en la Figura 1.

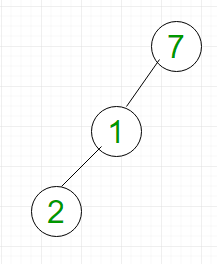
• Búsqueda: para buscar el elemento 2, tenemos que atravesar todos los elementos (suponiendo que hacemos un recorrido primero en anchura). Por lo tanto, la búsqueda en el árbol binario tiene una complejidad en el peor de los casos de O(n).
• Inserción: para insertar un elemento como hijo izquierdo de 2, tenemos que recorrer todos los elementos. Por lo tanto, la inserción en el árbol binario tiene una complejidad en el peor de los casos de O(n).
• Eliminación: para eliminar el elemento 2, tenemos que atravesar todos los elementos para encontrar 2 (suponiendo que hacemos un recorrido primero en anchura). Por lo tanto, la eliminación en el árbol binario tiene una complejidad en el peor de los casos de O(n).

Árbol de búsqueda binaria (BST):
BST es un tipo especial de árbol binario en el que el hijo izquierdo de un Node tiene un valor menor que el padre y el hijo derecho tiene un valor mayor que el padre. Considere el BST sesgado a la izquierda que se muestra en la Figura 2.

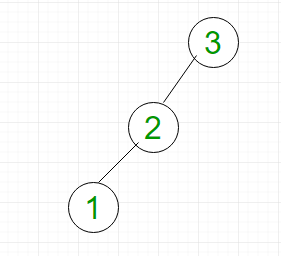
• Búsqueda: para buscar el elemento 1, tenemos que recorrer todos los elementos (en orden 3, 2, 1). Por lo tanto, la búsqueda en el árbol de búsqueda binaria tiene una complejidad en el peor de los casos de O(n). En general, la complejidad del tiempo es O(h) donde h es la altura de BST.
• Inserción: para insertar el elemento 0, debe insertarse como hijo izquierdo de 1. Por lo tanto, debemos recorrer todos los elementos (en orden 3, 2, 1) para insertar 0, que tiene la complejidad del peor de los casos de O (n). En general, la complejidad del tiempo es O(h).
• Eliminación: Para la eliminación del elemento 1, tenemos que recorrer todos los elementos para encontrar 1 (en orden 3, 2, 1). Por lo tanto, la eliminación en el árbol binario tiene una complejidad en el peor de los casos de O(n). En general, la complejidad del tiempo es O(h).

AVL/Árbol equilibrado en altura: el árbol
AVL es un árbol de búsqueda binaria con una propiedad adicional de que la diferencia entre la altura del subárbol izquierdo y el subárbol derecho de cualquier Node no puede ser superior a 1. Por ejemplo, el BST que se muestra en la Figura 2 no es AVL como diferencia entre el subárbol izquierdo y el subárbol derecho del Node 3 es 2. Sin embargo, el BST que se muestra en la Figura 3 es el árbol AVL.

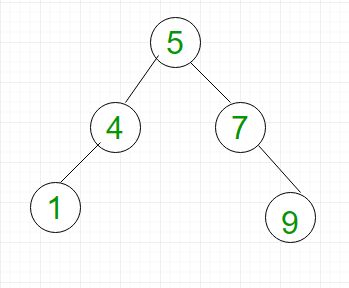
• Buscando: Para buscar el elemento 1, tenemos que recorrer los elementos (en orden 5, 4, 1) = 3 = log ₂ n. Por lo tanto, la búsqueda en el árbol AVL tiene una complejidad en el peor de los casos de O (log ₂ n).
• Inserción: para insertar el elemento 12, debe insertarse como hijo derecho de 9. Por lo tanto, necesitamos atravesar los elementos (en orden 5, 7, 9) para insertar 12, que tiene la complejidad del peor caso de O (log ₂ n).
• Borrado: Para borrar el elemento 9, tenemos que atravesar elementos para encontrar 9 (en orden 5, 7, 9). Por lo tanto, la eliminación en el árbol binario tiene una complejidad en el peor de los casos de O (log ₂ n).

Discutiremos preguntas basadas en las complejidades de las operaciones de árboles binarios.

Que-1. ¿Cuál es la complejidad de tiempo en el peor de los casos para las operaciones de búsqueda, inserción y eliminación en un árbol de búsqueda binario general?
(A) O(n) para todo
(B) O(Logn) para todo
(C) O(Logn) para buscar e insertar, y O(n) para borrar
(D) O(Logn) para buscar, y O( n) para insertar y borrar

Solución: Como se discutió, todas las operaciones en BST tienen una complejidad de tiempo en el peor de los casos de O(n). Entonces, la opción correcta es (A).

Que-2. ¿Cuáles son las complejidades de tiempo en el peor de los casos de búsqueda en árbol binario, BST y árbol AVL respectivamente?
(A) O(n) para todos
(B) O(Logn) para todos
(C) O(n) para árbol binario, y O(Logn) para otros
(D) O(n) para árbol binario y BST, y O (Iniciar sesión) para AVL

Solución: Como se discutió, la operación de búsqueda en el árbol binario y BST tienen una complejidad de tiempo en el peor de los casos de O(n). Sin embargo, el árbol AVL tiene una complejidad de tiempo en el peor de los casos de O (logn). Entonces, la opción correcta es (D).